Лекция 7. МЕТОД РУНГЕ-КУТТА РЕШЕНИЯ
Этот метод позволяет строить схемы различного порядка точности. Схемы Рунге-Кутта очень удобны как для расчетов на ЭВМ, так и для «ручных» расчетов. Сейчас они являются наиболее употребительными в практических вычислениях.
Построим семейство схем второго порядка точности и на его примере разберем основные идеи метода. В качестве исходного выражения возьмем ряд Тейлора
(20.1)
удерживая в нем член о (h 2), порядок которого равен предполагаемому порядку точности схемы. Чтобы избежать дифференцирования функции f (x, u), заменим производную 
конечной разностью. Так как первая производная 
то вторая производная 
будет равна
Соответственно выбирая значения 
После такой замены второй член в (20.1) можно формально объединить с первым, приведя (20.1) к следующему виду
(20.2)
(поскольку эта схема для расчета приближенного решения, мы снова употребляем обозначение уn вместо un). Здесь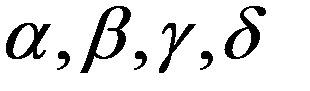 
- параметры, значения которых следует определить. Рассматривая правую часть (20.2) как функцию от h, разложим ее в ряд по степеням шага h
.
Выберем параметры 
так, чтобы это разложение было возможно более близко к ряду Тейлора (20.1). Очевидно, можно правильно передать два первых члена формулы Тейлора, если положить
Действительно 
значит при 
получаем второе слагаемое, а так как 
, то при 
получаем fx и для получения ffu надо положить 
.
Для определения четырех параметров получено только три уравнения, так что один параметр остается свободным. Выражая через 
остальные параметры и подставляя их в (20.2), получим однопараметрическое семейство двучленных схем Рунге-Кутта 
(20.3)
Выбрать параметр 
так, чтобы схема (20.3) правильно передавала и третий член формулы Тейлора (20.1), невозможно.
Погрешность этой схемы можно исследовать так же, как было сделано для схемы ломаных. При этом доказывается следующий результат. Если f (x, u) непрерывна и ограничена вместе со своими вторыми производными, то решение, полученное по схеме (20.3), равномерно сходится к точному решению с погрешностью О (max h 2 n), т.е. двучленная схема Рунге-Кутта имеет второй порядок точности.
Формула (20.3) имеет неплохую точность и нередко используется в численных расчетах. При этом обычно полагают либо 
=1, либо 
= 1/2.
| Рис. 20.1 |
| yn |
хn 
|
| хn |
| хn +1 |
| yn +1 |
| хn |
| хn +1 |
| yn |
| yn +1 |
| Рис. 20.2 |
В первом случае получается схема особенно простого вида
(20.4)
Ее смысл поясняется на рис. 20.1. Сначала делаем половинный шаг по схеме ломаных, находя 
Затем в найденной точке определяем наклон интегральной кривой 
По этому наклону определяем приращение функции на целом шаге 
Геометрическая интерпретация второго случая изображена на рис. 20.2
Здесь мы сначала грубо вычисляем по схеме ломаных значение функции 
и наклон интегральной кривой 
в новой точке. Затем находим средний наклон на шаге h: 
и по нему уточняем значение уn +1. Схемы такого типа называются «предиктор-корректор».
В таблице 20.1 приведен численный расчет по схеме (20.4) того же примера, который рассмотрен на прошлой лекции и приведен в таблице 19.1.
Таблица 20.1
| xn | yn | u (x) | Схема ломанных при h = 0,25 | |
| h = 1 | h = 0,5 | |||
| 0,5 1,0 | - 0,25 | 0,031 0,317 | 0,042 0,350 | 0,016 0,220 |
Таблица 20.1 заполняется следующим образом:
пусть 
тогда
Из таблицы видно, что схема второго порядка точности дает существенно лучшие результаты, чем схема ломаных. Уже расчет на грубой сетке с h = 0,5 можно считать удовлетворительным.
Методом Рунге-Кутта можно строить схемы различного порядка точности. Например, схема ломаных
есть схема Рунге-Кутта первого порядка точности. Наиболее употребительны схемы четвертого порядка точности, образующие семейство четырехчленных схем. Приведем без вывода ту из них, которая записана в большинстве стандартных программ ЭВМ
Схемы Рунге-Кутта имеют ряд важных достоинств:
а) все они (кроме схемы ломаных) имеют хорошую точность;
б) они являются явными, т.е. значение уn +1 вычисляется по ранее найденным значениям за определенное число действий по определенным формулам;
в) все схемы допускают расчет с переменным шагом, значит нетрудно уменьшить шаг там, где функция быстро меняется, и увеличить его в обратном случае;
г) для начала расчета достаточно выбрать сетку хn и задать значение 
.
Далее вычисления идут по одним и тем же формулам. Все эти свойства схем очень ценны при расчетах на ЭВМ.