Мы предполагаем уделить основное внимание случаю, когда у каждого из игроков имеется ровно две стратегии, т. е. случаю т = п = 2. Поэтому нам кажется уместным выписать приведенные выше формулы именно для такого случая.
В 2 ´ 2 биматричной игре платежные матрицы игроков имеют следующий вид
 ,
,  ,
,
вероятности
биматричная игра решение

а средние выигрыши вычисляются по формулам

где
 ,
, 
Сформулируем основное определение.
Определение. Будем считать, что пара чисел
 ,
,  ,
, 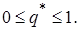
определяет равновесную ситуацию, если для любых р и q, подчиненных условиям  одновременно выполнены следующие неравенства
одновременно выполнены следующие неравенства

 (1)
(1)
Пояснение. Выписанные неравенства (1) означают следующее: ситуация, определяемая смешанной стратегией (р*, q*), является равновесной, если отклонение от нее одного из игроков при условии, что другой сохраняет свой выбор, приводит к тому, что выигрыш отклонившегося игрока может только уменьшиться. Тем самым, получается, что если равновесная ситуация существует, то отклонение от нее невыгодно самому игроку.
Теорема 1 (Дж. Нэш). Всякая биматричная игра имеет хотя бы одну равновесную ситуацию (точку равновесия) в смешанных стратегиях.
Итак, равновесная ситуация существует. Но как ее найти?
Если некоторая пара чисел (р*, q*) претендует на то, чтобы определять ситуацию равновесия, то для того, чтобы убедиться в обоснованности этих претензий, или, наоборот, доказать их необоснованность, необходимо проверить справедливость неравенств (1) для любого р в пределах от 0 до 1 и для любого q впределах от 0 до 1. В общем случае число таких проверок бесконечно. И, следовательно, действенный способ определения равновесной ситуации нужно искать где-то в ином месте.
Теорема 2. Выполнение неравенств

 (1)
(1)
равносильно выполнению неравенств



 (2)
(2)
Иными словами, для того, чтобы убедиться в обоснованности претензий пары (р*, q*) на то, чтобы определять равновесную ситуацию, нужно проверить справедливость неравенства

только для двух чистых стратегий игрока А (р = 0 и р = 1) и неравенства

только для двух чистых стратегий игрока В (q = 0 и q= 1).
Четыре неравенства (2) позволяют провести поиск точки равновесия вполне конструктивно.
Запишем средние выигрыши игроков А и В в более удобной форме.
Имеем

Обратимся к первой из полученных формул.
Полагая в ней сначала р = 1, а потом р = 0, получаем,

Рассмотрим разности


Полагая


получим для них следующие выражения


В случае, если пара (р, q) определяет точку равновесия, эти разности неотрицательны


Поэтому окончательно получаем

Из формул для функции нв (р, q) при q = 1 и q = 0 соответственно имеем

Разности
 и
и
с учетом обозначений

 .
.
приводятся к виду


совершенно так же, как соответствующие разности для функции НА.
Если пара (р, q) определяет точку равновесия, то эти разности неотрицательны


Поэтому

Вывод
Для того, чтобы в биматричной игре
 ,
,  ,
,
пара (р, q) определяла равновесную ситуацию, необходимо и достаточно одновременное выполнение следующих неравенств
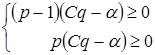 ,
,  ,
,
 ,
, 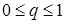 ,
,
где



 .
.