Раздел II. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
Лекция 2. ПОЛИНОМИАЛЬНЫЕ ФОРМУЛЫ
В классическом анализе производная от функции непрерывного аргумента определяется следующим образом:
В численных методах вместо отношения бесконечно малых, ограничиваются отношением конечных разностей. То есть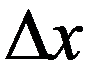 
фиксируется, предельного перехода не проводится (производная заменяется конечной разностью).
Некоторый отрезок 
делится на 
частей. Точки деления называются узлами. Узлы нумеруются от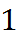 
до . 
Совокупность всех узлов называется сеткой. Сетка равномерная, то есть шаг сетки одинаковый и равный 
. В узлах сетки берутся значения функции. То есть составляется таблица соответствия каждому 
значение 
.
| 
| 
| 
| 
|
| 
| 
| 
| 
|
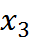
Производная от функции u в точке 1 будет выглядеть так:
Шаг 
обычно обозначается через 
. Точки на прямой (узлы) нумеруются 
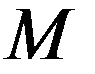, или 
, или 
. Тогда производные будут обозначаться:
или 
Если функция задана в узлах сетки (так называемая сеточная функция), то можно построить интерполяционный многочлен Ньютона, а затем продифференцировать этот многочлен.
Берём его первую производную
Входящие в эту формулу разделённые разности имеют вид
.
Видно, что по этим формулам можно вычислять первую производную по двум узлам, по трём узлам, по четырём узлам и по пяти узлам. Для получения первой производной по большему количеству узлов, нужно дифференцировать интерполяционный многочлен Ньютона, построенный по большему числу узлов.
Порядок точности многочлена Ньютона равен количеству узлов интерполяции. Порядок точности производной равен количеству узлов интерполяции минус порядок производной. Значит по двум узлам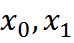 
первая производная будет иметь первый порядок точности.
; 
.
А вот в центральной токе 
первая производная будет иметь второй порядок точности, потому что центр симметрии всегда увеличивает порядок точности на одну единицу. Значит производная
имеет второй порядок точности.
Найдём первую производную в точке 
по трём узлам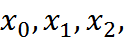 
используя продифференцированный многочлен Ньютона.
Таким же образом можно найти первую производную в любой точке промежутка 
, используя описанную процедуру. Порядок точности первой производной будет вторым.
Дифференцируя многочлен Ньютона второй раз, можно будет по нему находить вторую производную и так далее.
Например, найдём вторую производную в точке по трём узлам 
,
.
Порядок точности этой формулы равен 1. Очевидно в точках 
вторая производная будет иметь тот же вид, но в точке она будет иметь второй порядок точности.
ПРАКТИЧЕСКОЕ ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ
При вычислении производной функции, заданной таблицей, следует иметь ввиду, что лучший способ найти производную 
по двум значениям функции – это взять такие значения справа и слева на равном расстоянии от того значения х, для которого мы хотим подсчитать величину производной и воспользоваться простейшей формулой
.
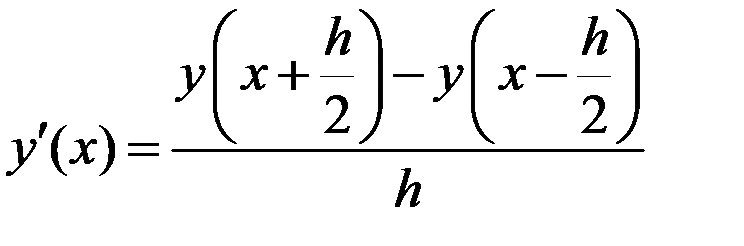Таким образом, если даны значения у для значений х, расположенных через равные промежутки (т.е. в арифметической прогрессии), то удобно вычислять производные в серединах промежутков. Другими словами, если значения у были заданы для «целых» значений х, то значения 
будут подсчитаны для «полуцелых» значений х. По значениям 
можно таким же способом найти производную от 
, т.е. 
. При этом, значения 
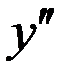получатся снова для целых значений х. Можно выразить 
непосредственно через 
Если же нужны значения 
для других х, то их можно получить интерполяцией.
На практике (в частности в ракетной технике) табличные функции возникают при проведении экспериментов. Здесь в качестве аргумента х – как правило, выступает время t. А в качестве функции – любая замеряемая величина: давление, температура и т.д. Суть таблиц такова. Через равные промежутки времени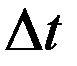 
снимается показание датчика (т.е. значение давления или температуры в момент времени t).
В связи с этим, очень важные вопросы здесь возникают в связи с ограниченной точностью и ошибками, присущими каждому измерению.
При вычислении производной разность двух значений у делится, на 
. Чем меньше промежуток 
, т.е. чем меньше знаменатель, тем большую ошибку в величину производной вносит данная ошибка в каждом измеренном значении у. Поэтому производная функции, заданной экспериментальными значениями, оказывается известной с меньшей точностью, чем сама эта функция.
Поясним это на графике. На рис. 12.1 изображены две кривые – одна нарисована сплошной линией, другая – пунктирной. Сплошная кривая – это график функции у = х - 0,1 х 2, пунктирная – график функции у 1 = х – 0,1 х 2 + 0,5 е 
.
| у |
| х |
| Рис. 12.1 |
На рис. 12.2 показаны графики производных 
и 
1.
|
| х |
| Рис. 12.2 |
Еще сильнее разнятся вторые производные. Их графики изображены на рис. 12.3.
| 6
|
| х |
| Рис. 12.3 |
| -2 |
| -4 |
| -6 |
| -8 |
Так, в случае, когда кривая получена из опыта, небольшое изменение хода кривой на каком – либо промежутке может быть вызвано результатом ошибки отдельного опыта. Из предыдущего примера мы видели, что эти ошибки сильно влияют на производные, особенно высших порядков.
Для того, чтобы получить надёжные значения производной, нужно сперва подобрать формулу, хорошо описывающую опытные данные (скажем, методом наименьших квадратов), а затем находить производную, пользуясь этой формулой.
Так как формула в методе наименьших квадратов строится с учетом всех опытных данных, то значение производной при каждом значении х будет найдено по формуле с учётом всех данных, а не только двух-трёх ближайших. Поэтому естественно ожидать, что случайные ошибки в отдельных измерениях меньше скажутся на величине производной.