Приближённые методы вычисления определённых интегралов.
Есть приближённые методы вычисления определённых интегралов. Отрезок интегрирования 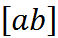 делится на
делится на 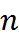 частей. Точки деления называются узлами. Узлы нумеруются от
частей. Точки деления называются узлами. Узлы нумеруются от  до
до 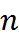 .
. 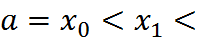
 Совокупность всех узлов называется сеткой. Сетка равномерная, то есть шаг сетки одинаковый и равный
Совокупность всех узлов называется сеткой. Сетка равномерная, то есть шаг сетки одинаковый и равный 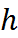 . В узлах сетки берутся значения интегрируемых функций. То есть составляется таблица соответствия каждому
. В узлах сетки берутся значения интегрируемых функций. То есть составляется таблица соответствия каждому 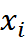 значение
значение  .
.
| 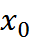
| 
| 
| 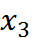
|

| 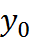
| 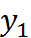
| 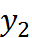
| 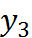
|
После составления таблицы по квадратурным формулам приближённо вычисляются интегралы. Самая простая квадратурная формула  это формула прямоугольников.
это формула прямоугольников.
1. Формула левых прямоугольников имеет вид:
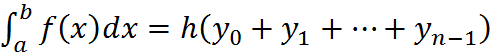 .
.
2. Формула правых прямоугольников имеет вид:
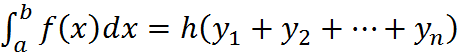 .
.
Эти формулы точны на полиномах (многочленах) нулевой степени, т.е. на константах. Поэтому говорят, что эта формула имеет первый порядок точности.
3. Формула средних. В этой формуле значения функций берутся в серединах между узлами.
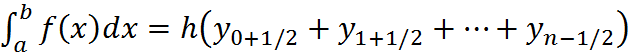 .
.
Эта формула точна на полиномах первой степени, т.е. на функциях 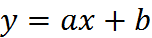 . Поэтому говорят, что эта формула имеет второй порядок точности.
. Поэтому говорят, что эта формула имеет второй порядок точности.
4. Формула трапеций имеет вид:
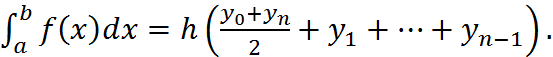
Эта формула также как и формула средних точна на полиномах первой степени, т.е. на функциях 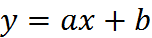 . Поэтому говорят, что эта формула имеет второй порядок точности.
. Поэтому говорят, что эта формула имеет второй порядок точности.
4. Формула Симпсона имеет вид:


Эта формула точна на полиномах третьей степени, т.е. на функциях 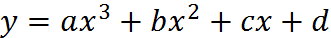 . Поэтому говорят, что эта формула имеет четвёртый порядок точности.
. Поэтому говорят, что эта формула имеет четвёртый порядок точности.
Примеры.
1). Вычислить интеграл 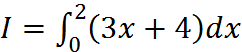 .
.
Решение.
а). Вычислим интеграл по формуле средних. Для этого разобьём отрезок интегрирования на 2 части, т.е. положим 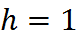 и наша сетка будет содержать узлы
и наша сетка будет содержать узлы 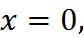

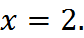 Найдём значения функции в серединах между узлами:
Найдём значения функции в серединах между узлами:
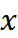
| 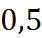
| 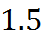
|

| 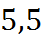
| 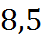
|
Применяя формулу средних, вычислим интеграл:
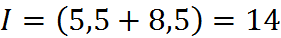 .
.
Найдём точное значение интеграла:
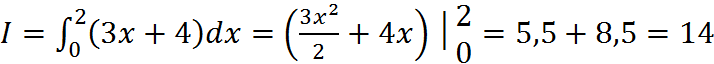 .
.
То есть мы показали, что формула средних точна на полиномах первой степени.
б). Вычислим этот же интеграл по формуле трапеций. Для этого разобьём отрезок интегрирования на 2 части, т.е. положим 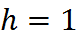 и наша сетка будет содержать узлы
и наша сетка будет содержать узлы 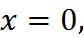

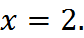 Найдём значения функции в узлах сетки:
Найдём значения функции в узлах сетки:
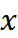
| 
| 
| 
|

| 
| 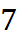
| 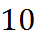
|
Применяя формулу трапеций, вычислим интеграл:
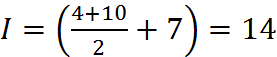 .
.
То есть мы показали, что формула трапеций также точна на полиномах первой степени.
Вычислить интеграл
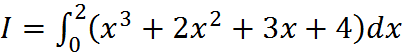 .
.
Решение. Вычислим интеграл по формуле Симпсона. Для этого разобьём отрезок интегрирования на 2 части, т.е. положим 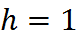 и наша сетка будет содержать узлы
и наша сетка будет содержать узлы 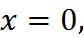

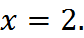 Найдём значения функции в узлах сетки:
Найдём значения функции в узлах сетки:
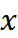
| 
| 
| 
|

| 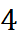
| 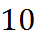
| 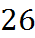
|
Применяя формулу Симпсона, вычислим интеграл:
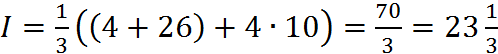 .
.
Найдём точное значение интеграла:
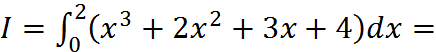
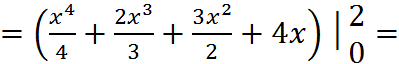
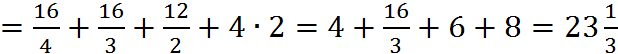 .
.
То есть мы показали, что формула Симпсона точна на полиномах третьей степени.
Вычисление кратных интегралов
Метод ячеек. Рассмотрим двукратный интеграл по прямоугольнику
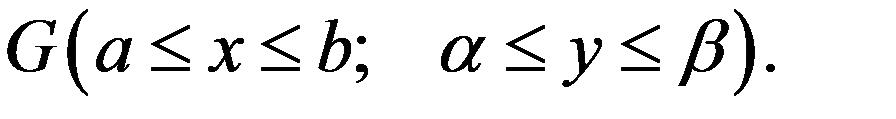
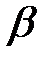 в в
|
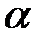
|
| а |
| b |
| х |
| Рис. 14.2 |
| y |
 Тогда интеграл легко вычисляется
Тогда интеграл легко вычисляется
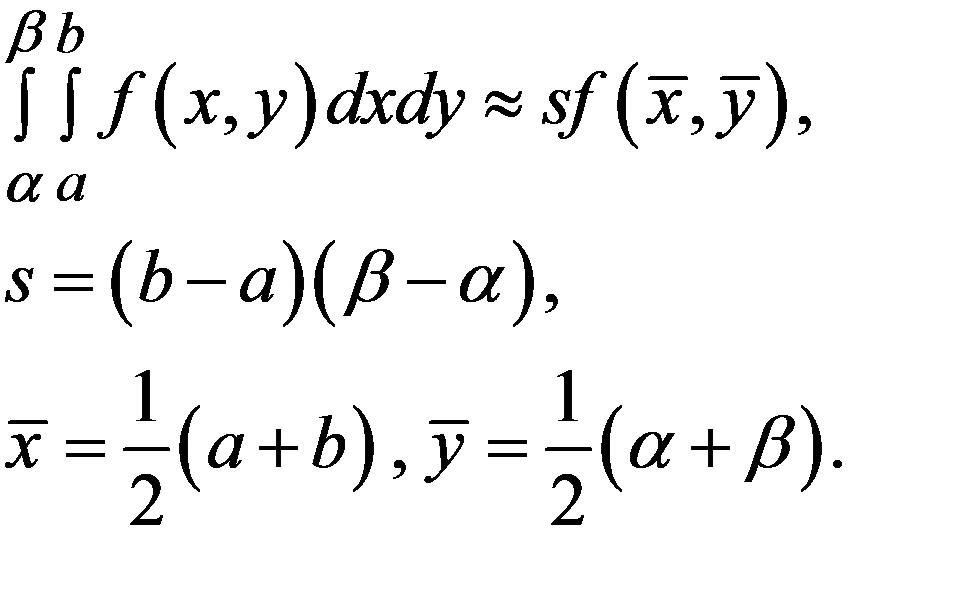 (14.4)
(14.4)
Это, как видите, двумерная формула средних. Для повышения точности можно разбить область на прямоугольные ячейки (рис. 14.2) Приближенно вычисляя интеграл в каждой ячейке по формуле средних и обозначая  соответственно площадь ячейки и координаты ее центра масс, получим обобщенную формулу средних
соответственно площадь ячейки и координаты ее центра масс, получим обобщенную формулу средних
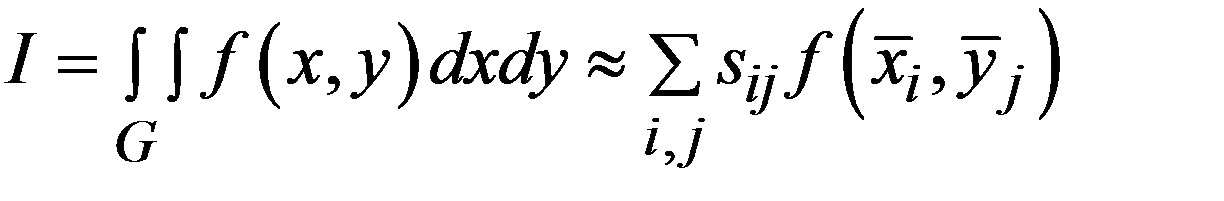 . (14.5)
. (14.5)
Справа стоит интегральная сумма; следовательно, для любой непрерывной функции f (x, y) она сходится к значению интеграла, когда периметры всех ячеек стремятся к нулю.