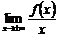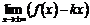Правило исследования функции на выпуклость (вогнутость) и определения точек перегиба

Исследование функции с помощью производной

Справочный материал

Монотонность функции

Определение. Функция y = f(x) возрастает (убывает) на промежутке Х, если " х ₁, х ₂Î Х: х ₂> х ₁ Þ f(х ₂ ) > f(х ₁ ) (f(х ₂ ) < f(х ₁ )).

Теорема 1. (необходимое условие монотонности). Если дифференцируемая на (a;b) функция y = f(x) возрастает (убывает),

то f ¢(x)≥0 (f ¢(x)≤0), " x Î(a;b).

Теорема 2. (достаточное условие монотонности). Если y = f(x) дифференцируема на (a;b) и " x Î(a;b): f ¢(x)>0 (f ¢(x)<0), то функция на (a;b) возрастает (убывает).

Экстремумы функции

Определение. Точка х ₀ называется точкой локального max (min) функции y=f(x), если ∃ О_d(х ₀): f(х ₀ ) > f(х) (f(х ₀ ) < f(х)), " x ÎО_d(х ₀).

Точки локального max (min) – это точки локального экстремума, а значения функции в этих точках - экстремумы функции.

Теорема 3. (необх. условие экстремума). Если дифференцируемая функция y=f(x) имеет в точке х ₀ экстремум, то f ¢(х ₀)=0.

Замечания:

1. Существуют функции, которые в точке экстремума не имеют производной (не дифференцируемы), например, y =| x | в точке х ₀=0.

2. Обратная теорема неверна, например, для y=x ³ в точке х ₀=0.

Т.о. непрерывная функция может иметь экстремум в точках, где f ¢(х)=0 или ∄ f ¢(х), т.е. в критических точках 1 рода.

Теорема 4. (первое достаточное условие экстремума). Если непрерывная функция y=f(x) дифференцируема в некоторой окрестности точки х ₀ и при переходе через нее f ¢ меняет знак с «+» на «-» (с «-» на «+»), то х ₀– точка max (min).

Теорема 5. (второй достаточный признак экстремума). Если функция y=f(x) дважды дифференцируема в некоторой окрестности точки х ₀ и выполняются условия, то

1. 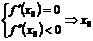- точка max 2. - точка min.

Замечание. Если f ¢¢(х ₀)=0 (∄ f ¢¢(х ₀)), то второй признак неприменим. Также признак неудобен при громоздкой форме f ¢¢(х).

Правило исследования y=f(x) на монотонность и экстремумы

1. Найти D_f.

2. Вычислить f ¢(х) и найти критические точки 1 рода (f ¢(х)=0 или ∄ f ¢(х)).

3. Определить знак f ¢(х) в промежутках, на которые критические точки делят D_f (определить промежутки знакопостоянства функции

y=f ¢(х)).

4. Найти интервалы возрастания и убывания функции, точки экстремума. Вычислить экстремумы функции.

Выпуклость графика функции. Точки перегиба

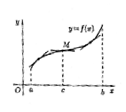Определение. График функции называется выпуклым (вогнутыми) на интервале (a;b), если он расположен ниже (выше) любой ее касательной на этом интервале.

Определение. Точки графика непрерывной функции, отделяющие его части выпуклости и вогнутости, называются точками перегиба.

Теорема 6. Если функция y=f(x) дважды дифференцируема на (a;b) и f ¢¢(х)<0 (f ¢¢(х)>0), " x Î(a;b), то график функции y=f(x) на (a;b) является выпуклым (вогнутым).

Теорема 7. (достаточное условие существования точки перегиба). Если f ¢¢(х) при переходе через точку x ₀ (в которой f ¢¢(x ₀)=0 или ∄ f ¢¢(x ₀)) меняет знак, то x ₀ – точка перегиба.

Правило исследования функции на выпуклость (вогнутость) и определения точек перегиба

1. Найти D_f.

2. Вычислить f ¢¢(х) и найти критические точки 2 рода (f ¢¢(х)=0 или ∄ f ¢¢(х)).

3. Определить знак f ¢¢(х) в промежутках, на которые критические точки делят D_f.

4. Найти найти интервалы выпуклости и вогнутости, точки перегиба.

4. Асимптота графика функции y=f(x) – это прямая, расстояние до которой от точки М, лежащей на графике, стремится к нулю при удалении точки М от начала координат по кривой.