1. Найти Df. Определить точки разрыва функции.
2. Найти точки пересечения графика функции с осями координат.
3. Если Df симметрична относительно точки x =0, исследовать y=f(x) на четность.
4. Исследовать функцию на периодичность.
5. Найти асимптоты.
6. Найти интервалы монотонности и экстремумы функции.
7. Найти промежутки выпуклости и точки перегиба.
8. Построить график функции (при построении найти дополнительные точки, уточняющие график).
6.Наибольшее и наименьшее значения функции y = f (x) на отрезке [ a;b ]
1. Найти Df.
2. Определить критические точки 1 рода (f ¢(х)=0 или ∄ f ¢(х)), принадлежащие отрезку [ a;b ].
3. Вычислить значения функции в найденных критических точках и на концах отрезка.
4. Из полученных значений функции выбрать наибольшее (наименьшее).
7.Применение производной в задачах с экономическим содержанием
Предельные величины
y = f(x) Þ 
- средняя величина (отношение суммарной величины к независимой переменной)
f ¢(х) - предельная величина (скорость изменения f относительно x).
С=С(х) - функция издержек производства (х - объем выпускаемой продукции, С - издержки производства)
Þ 
- средние издержки (издержки на 1 единицу выпускаемой продукции)
С ¢(х) - предельные издержки (прирост затрат на производство 1 единицы дополнительной продукции).
Эластичность функции
y=f(x) Þ E x (y)= 
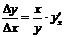- эластичность показывает, на сколько % изменится y при изменении x на 1 %.
D=D(p) - функция спроса Þ E p (D)= 
- коэффициент эластичности спроса
S=S(p) - функция предложения Þ E p (S)= 
- коэффициент эластичности предложения.
Задачи
1. Найти интервалы монотонности и экстремумы функции
а) 
б) 
в) 
г) 
д) 
е) 
ж) 
з) 
.
2. Найти интервалы выпуклости (вогнутости) функции и точки перегиба
а) 
б) 
в) 
г) 
д) 
е) 
.
3. Найти асимптоты графика функции
а) 
б) 
в) 
г) 
д) 
е) 
.
4. Исследовать функцию и построить график
а) 
б) 
в) г) 
д) 
е) 
ж) 
з) 
.
5. Найти наибольшее и наименьшее значение функции на отрезке
а) 
б) 
в) 
г) 
д) 
е) 
[-3;3] [0;3] [-2;4] [0;π] [-1;1] [-4;4].
6. Разность двух чисел 13. Каковы должны быть эти числа, чтобы их произведение было наименьшим?
7. Забором длиной 24 метра требуется огородить с трех сторон прямоугольный участок наибольшей площади. Определить размеры участка.
8. Зависимость между издержками производства С (ден.ед.) и объемом выпускаемой продукции Q (ед.) задана формулой C = 40 Q – 0,08 Q3. Определить средние и предельные издержки при объеме продукции, равном 15 единиц.
9. Зависимость издержек производства С от объема выпуска продукции Q выражает формула C = 30 Q – 0,03 Q3. Определить средние и предельные издержки при объеме продукции: а) Q =10 ед.; б) Q =5 ед. Дать заключение о необходимости расширения производства для данной функции издержек.
10. Выручка от продажи конфет составляет Р(х) = 50-0,5х2, где x -объем проданной продукции (тыс.ед.). Найти среднюю и предельную выручку, если продано: а) 10 тыс.ед. продукции; б) 60 тыс.ед. продукции.
11. Функции спроса и предложения на товар заданы формулами D(p) = 7-p, S(p) = 3p-1. Найти:
а) равновесную цену
б) E p (D), E p (S) при равновесной цене
в) изменение дохода (в %) при увеличении равновесной цены на 5 %;
г) сумму налогового сбора, поступающую в бюджет, если на товар введен косвенный налог, уплачиваемый в размере 4 ден.ед. на 1 ден.ед. товара. Выполнить графическую иллюстрацию.
д) объемы налогового бремени продавца и покупателя. Как это согласуется с эластичностью D и S.
12. Функции спроса и предложения заданы формулами D(p) = 9-p, S(p) = p+1. Найти:
а) равновесную цену
б) E p (D), E p (S) при равновесной цене
в) изменение дохода (в %) при увеличении равновесной цены на 10 %
г) сумму налогового сбора при введении косвенного налога в размере 2 ден.ед. на 1 ден.ед. товара. Выполнить графическую иллюстрацию
д) объемы налогового бремени покупателя и продавца.