Плоское напряжённое состояние. Круги Мора.

Статически неопределимые системы. Значение статической неопределимости.

Статически неопределимыми называются такие системы, опорные реакции в которых и внутренние усилия невозможно определить только из уравнений статики (уравнений равновесия). По сравнению с системами статически определимыми указанные системы имеют дополнительные связи, которые называют лишними связями. Усилия, возникающие в лишних связях, называют лишними неизвестными.

Термин «лишние» следует понимать как «избыточные», а не как «ненужные». Наличие лишних связей делает систему более жёсткой и более экономичной.

Степенью статической неопределимости n называется разность между числом неизвестных искомых усилий Н и числом независимых уравнений равновесия У для их нахождения: n = Н – У.

На рис. 10.1 показаны системы один раз статически неопределимые: балка, для которой можно составить три уравнения равновесия при четырёх неизвестных реакциях R ₁– R ₄; шарнирно-стержневая система, для которой можно составить два уравнения равновесия при трёх неизвестных усилиях N ₁– N ₃; вал, для которого можно составить одно уравнение равновесия при двух неизвестных моментах М ₁ и М ₂.

Рис. 10.1. Статически неопределимые системы:
а – при изгибе; б – при растяжении; в – при кручении

Статическая неопределимость обусловлена наличием избыточных связей, превышающих минимум связей, необходимых для образования геометрически неизменяемой статически определимой системы. Число избыточных связей называют степенью статической неопределимости, которую можно вычислить как разность чисел неизвестных сил и уравнений равновесия.

Плоское напряжённое состояние. Круги Мора.

Если все векторы напряжений параллельны одной и той же плоскости, напряженное состояние называется плоским (рис. 1). Иначе: напряженное состояние является плоским, если одно из трех главных напряжений равно нулю.

Рисунок 1.

Плоское напряженное состояние реализуется в пластине, нагруженной по ее контуру силами, равнодействующие которых расположены в ее срединной плоскости (срединная плоскость - плоскость, делящая пополам толщину пластины).

Направления напряжений на рис. 1 приняты за положительные. Угол α положителен, если он откладывается от оси х к оси у. На площадке с нормалью n:

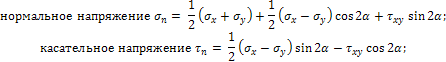
(1)

при .

Нормальное напряжение σ_n положительно, если оно растягивающее. Положительное напряжение показано на рис. 1. Правило знаков для по формуле (1) то же самое, что для напряжений по формуле (1).

Зависимость напряжений σ_n и τ_n, действующих на площадку с нормалью n, проходящую через рассматриваемую точку, можно представить наглядно графически при помощи круговой диаграммы Мора (кругов Мора).

Заданы главные напряжения σ₁ и σ₂ ( см. рис. 2 ). Откладываются отрезки ОA=σ₁ и ОВ=σ₂ с учетом знаков (рис. 1). На отрезке АВ, как на диаметре, строится окружность. Из точки В проводится прямая под углом α к оси σ. Координаты точки D пересечения этой прямой с окружностью дают напряжения по наклонной площадке: ОЕ=σ_n, ED=τ_n.

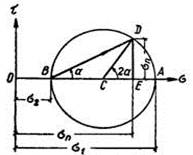Рисунок 1.

Заданы напряжения α_х, σ_y, τ_ху (рис. 2). Откладываются отрезки ОЕ=σ_х и OF=σ_y с учетом знаков. Из точки Е (независимо от ее положения) откладывается отрезок ED=τ_xy также с учетом знака. Из точки С, делящей отрезок EF пополам, как из центра строится окружность радиусом CD. Прямая BD определяет направление действия вектора главного напряжения σ₁, а абсциссы точек пересечения окружности с осью σ дают величины главных напряжений: OА=σ₁, ОВ=σ₂.

Рисунок 2.