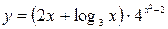Раздел 3 - Дифференциальное исчисление
Тема 1. Понятие производной функции в точке. Формулы производных.
Понятие производной является одним из основных математических понятий. Производная широко используется при решении целого ряда задач математики, физики, других наук.
Определение 1. Производной функции  в точке
в точке  называется предел отношения приращения функции к приращению аргумента, при стремлении приращении аргумента к нулю
называется предел отношения приращения функции к приращению аргумента, при стремлении приращении аргумента к нулю  , где для функции
, где для функции  определяется производная
определяется производная 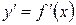 .
.
Функция  , имеющая производную в каждой точке интервала
, имеющая производную в каждой точке интервала  , называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.
, называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.


Физический смысл:
 .
.
Геометрический смысл:
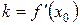 – угловой коэффициент касательной, проведенной
– угловой коэффициент касательной, проведенной
к графику функции  в точке касания
в точке касания  ;
;
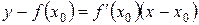 – уравнение касательной;
– уравнение касательной;
 – угловой коэффициент нормали к графику функции;
– угловой коэффициент нормали к графику функции;
 – уравнение нормали.
– уравнение нормали.

Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.
Формулы дифференцирования
Основные правила
1. 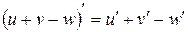 ;
;
2. 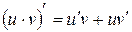 ;
;
3.  ;
;
4. 
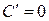



| 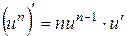
|

| 
|

| 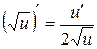
|

| 
|

| 
|

| 
|

| 
|

| 
|
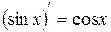
| 
|

| 
|

| 
|

| 
|

| 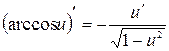
|

| 
|

| 
|
Рассмотрим примеры.
1. Точка движется по закону  .
.
Найти скорость в момент времени  .
.
Решение: 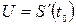

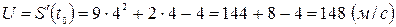 .
.
2. Составить уравнение касательной и уравнение нормали, проведенных к графику функции  в точке
в точке  .
.
Решение
Уравнение касательной:  ;
;
Уравнение нормали: 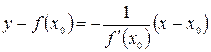 .
.
 ;
;
 ;
;


 .
.
Уравнение касательной
 ;
;
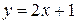 .
.
Уравнение нормали:
 ;
;
 .
.
Упражнения
№1. Найдите производные следующих функций.
а)  ; к)
; к) 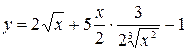 ;
;
б)  ; л)
; л)  ;
;
в)  ; м)
; м)  ;
;
г)  ; н)
; н)  ;
;
д)  ; 0)
; 0)  ;
;
е)  ; п)
; п)  ;
;
ж)  ; р)
; р)  ;
;
з)  ; с)
; с)  .
.
и)  ;
;
№2. Составить уравнение касательной и нормали к графику функции в точке  .
.
а) 
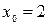 ;
;
б) 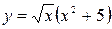
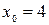 ;
;
в) 
 .
.
№3. Точка движется по закону  . Найдите значение скорости в момент времени
. Найдите значение скорости в момент времени  .
.
Тема 2. Нахождение производных сложных функций
 - сложная функция.
- сложная функция.
 - сложная функция.
- сложная функция.
Производная сложной функции  вычисляется по формуле
вычисляется по формуле  .
.
Например:
 ;
;
 ;
;
 ;
;
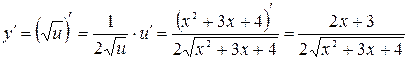 ;
;
 ;
;
 ;
;

 .
.
Упражнения
№1. Найдите производные следующих функций:
1)  ; 8)
; 8) 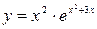 ;
;
2) 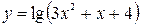 ; 9)
; 9) 
3)  ; 10)
; 10)  ;
;
4)  ; 11)
; 11)  ;
;
5) 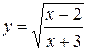 ; 12)
; 12)  ;
;
6)  ; 13)
; 13)  ;
;
7)  ; 14)
; 14) 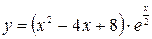 ;
;
15)  ; 21)
; 21)  ;
;
16)  ; 22)
; 22)  ;
;
17)  ; 23)
; 23) 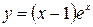
18)  ; 24)
; 24) 
19)  ; 25)
; 25)  .
.
20)  ;
;
Тема 3. Дифференциал функции и его нахождение
Пусть функция  , где
, где 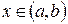 дифференцируема в некоторой точке
дифференцируема в некоторой точке 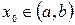 , т.е. функция
, т.е. функция  имеет производную в этой точке
имеет производную в этой точке


бесконечно малая величина,
при 



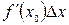 - главная часть приращения функции, которая называется дифференциалом функции и обозначается:
- главная часть приращения функции, которая называется дифференциалом функции и обозначается: 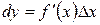 .
.
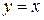
 .
.
Определение: Дифференциал функции – величина равная произведению производной этой функции на дифференциал аргумента  .
.
Например:
 ;
;
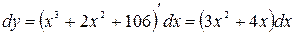 ;
;

|

 .
.

Например:
Найти приближенное функции 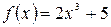 в точке
в точке  .
.
Решение
используем формулу
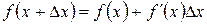 ;
;
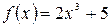 4;
4;
 ;
;
 ;
;
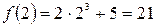 ;
;
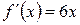 ;
;
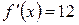 ;
;
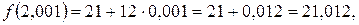
если  .
.
Формулы для приближенных вычислений
1)  ;
;
2)  ;
;
3)  .
.
Например
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  .
.
Упражнения
№1. Найти дифференциал следующих функций:
1) 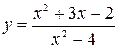 ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ;
;
8) 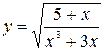 ; 9)
; 9)  ; 10)
; 10) 
 .
.
№2. Вычислить приближенное значение функции:
1)  ;
;
2)  ;
;
3)  .
.
№3. Вычислите приближенное значение следующих выражений:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8) 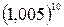 ; 9)
; 9)  ;
;
10)  ; 11)
; 11)  ; 12)
; 12)  ;
;
13)  ; 14)
; 14)  ; 15)
; 15)  ;
;
16) 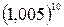 .
.
Тема 4. Наибольшее и наименьшее значение функции
На промежутке.
Задачи на максимум и минимум
Рассмотрим функцию  .
.
Для нахождения наибольшего и наименьшего значения функции, непрерывной в некотором промежутке, необходимо:
1. Найти производную.
2. Приравнять производную к нулю, т.е. найти критические точки.
3. Найти значение функции на концах промежутка и в критических точках, принадлежащих данному промежутку.
4. Выбрать наибольшее и наименьшее значение функции на данном промежутке.
Например:
Найти наибольшее и наименьшее значение функции 
на промежутке 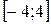 .
.
1. 
2. 
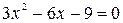 ;
;
 ;
;
 ;
;
 .
.
3. 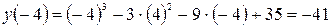 ;
;
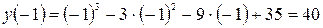 ;
;
 ;
;
 ;
;
 .
.
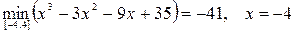 .
.
Рассмотрим задачу
Из квадратного листа жести со стороной 36 м надо изготовить ящик, открытый сверху с квадратным основанием наибольшего объема. Найти этот объем.

Обозначим за  длину стороны вырезаемого квадрата, тогда сторона основания будет равна
длину стороны вырезаемого квадрата, тогда сторона основания будет равна  . Следовательно, объем будет вычисляться по формуле
. Следовательно, объем будет вычисляться по формуле  .
.
Т.к. в основании ящика квадрат, тогда  , а
, а 
 .
.
1. 
 .
.
2.  ;
;
 ;
;
 ;
;
 .
.
 |

 ;
; 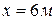 .
.
Упражнения
№1. Найдите наибольшее и наименьшее значение следующих функций на заданных промежутках:
1.  ;
;
2.  ;
;
3.  .
.
№2. Сумма двух положительных чисел равна 5. Каковы эти числа, если сумма их кубов является наименьшей.
№3. Сумма основания и высоты треугольника равна 12 см. Каким должно быть основание треугольника, чтобы площадь треугольника была наибольшей?
№4. Из шара радиуса R выточить цилиндр наибольшего объема. Найдите размеры этого цилиндра.
№5. Произведение двух положительных чисел равно 16. Чему равны эти числа, если их сумма наименьшая.
№6. Из листа картона 80 х50 см, требуется изготовить коробку открытую сверху наибольшей вместимости. Найти объем коробки.
№7. На какой высоте надо повесить фонарь над центром круглой площадки радиуса 20 см, чтобы площадка была максимально освещена у границы. Ъ
№8. Из всех прямоугольников данного периметра 60 см, найти тот, у которого площадь наибольшая.
Зачетная работа по теме
«Дифференциальное исчисление»
№1. Проволокой длиной 100 м нужно оградить прилегающую к дому прямоугольную площадку наибольшей площади. Установить размеры площадки.
№2. Вычислить:
 ;
;  ;
; 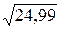 .
.
№3. Найдите дифференциал следующих функций:
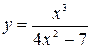 ;
;  ;
;