Допущено учебно-методическим объединением
по профессиональному образованию в качестве
учебного пособия для студентов высших учебных заведений, обучающихся по специальности «Машиностроение
и технологическое оборудование»
Издательство
Пермского государственного технического университета
УДК 620.10
С64
Рецензенты:
эксперт УМО по ППО, зам. директора инженерно-педагогического института РГППУ,
кандидат физико-математических наук А.В. Песков;
действительный член РАЕН
доктор технических наук, профессор Г.Л. Колмогоров
С64 Сопротивление материалов: учеб. пособие / Н.Н. Вассерман, А.П. Жученков, М.Л. Зинштейн, А.М. Ханов. – Пермь: Изд-во Перм. гос. техн. ун-та, 2011. – 343 с.
ISBN 978-5-88151-732-8
Содержатся разделы: растяжение-сжатие, кручение, геометрические характеристики, изгиб, статически неопределимые системы, теория напряженного состояния, сложное сопротивление, усталость материалов, устойчивость, оболочки (безмоментная теория), задачи динамики.
УДК 620.10
ISBN 978-5-88151-732-8 © ГОУ ВПО «Пермский государственный
 |
технический университет», 2011
Глава 1. Введение В НАУКУ
О СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
1.1. Общие определения
При проектировании инженерных сооружений и машин вопрос о выборе размеров отдельных частей с позиции прочности играет весьма важную роль. Для решения этой задачи следует, прежде всего, выяснить те внешние усилия, которые действуют на сооружения, затем по этим силам необходимо определить внутренние усилия, возникающие в частях сооружений
и машин. Для обеспечения прочности и долговечности сооружения нужно выбрать размеры частей так, чтобы внутренние усилия не превосходили известных норм, устанавливаемых для различных материалов на основании опытного исследования их прочности.
Сопротивление материалов – это наука об инженерных методах расчета на прочность, жесткость и устойчивость элементов машин и сооружений.
Под прочностью понимают способность конструкции, ее частей и деталей выдерживать определенную нагрузку, не разрушаясь.
В отличие от курса теоретической механики, сопротивление материалов наделяет реальные тела свойствами деформируемости – изменяемости геометрических размеров и формы. В связи с этим кроме расчетов на прочность во многих случаях проектирования производят расчеты на жесткость и устойчивость.
Под жесткостью подразумевают способность конструкции и ее элементов противостоять внешним нагрузкам с точки зрения деформаций (изменения формы, размеров).
Под устойчивостью понимается способность конструкции сохранять первоначальную форму упругого равновесия при воздействии внешних нагрузок.
Сопротивление материалов рассматривает методы расчетов элементов конструкции и вопросы расчета некоторых простейших конструкций. Вопросами расчетов на прочность, жесткость и устойчивость самих конструкций занимается строительная механика.
В методических указаниях и контрольных заданиях данного пособия рассматриваются схематизированные типовые элементы машиностроительных, строительных, транспортных и других конструкций, прочность, жесткость и устойчивость которых
и предлагается рассчитать.
Основная цель настоящего пособия – помочь студентам освоить методики и приобрести навыки расчетов по различным разделам курса «Сопротивление материалов».
1.2. Основные понятия. Метод сечения
Основными понятиями науки о сопротивлении материалов являются понятия реального объекта и расчетной схемы, внешних и внутренних силовых факторов, геометрических характеристик, напряжений (полное, нормальное, касательное), деформаций и перемещений (линейные, угловые). Сюда относятся также основные физические законы, общие гипотезы и методы, при помощи которых устанавливаются зависимости между этими понятиями.
При выборе расчетной схемы в геометрию реального объекта вводятся упрощения.
Основным упрощающим приемом в сопротивлении материалов является приведение геометрической формы тела к схеме стержня, оболочки, пластины, массива.
Под стержнем понимается тело, одно из измерений которого (длина) значительно больше двух других. Геометрия стержня может быть образована путем перемещения плоской фигуры вдоль некоторой кривой. Эта кривая называется осью стержня, а плоская фигура, имеющая свой центр тяжести на оси и нормальная к ней, называется поперечным сечением. Для стержня обозначим продольную ось – z, в поперечном сечении главные оси – x и y.
Оболочка – такое геометрическое тело, у которого одно из измерений (толщина) значительно меньше других (радиусов кривизны и габаритных размеров). К оболочкам могут быть отнесены стенки баков, купола и др.
Как и всякая наука, сопротивление материалов идет от простого к сложному, решая сначала элементарные задачи растяжения-сжатия, сдвига, изгиба и кручения, а затем используя эти решения для более сложных задач.
Внешние силы, действующие на реальный объект, чаще всего известны. Обычно необходимо определить внутренние силы (результат взаимодействия между отдельными частями данного тела), которые неизвестны по величине и направлению, но знание которых необходимо для прочностных и деформационных расчетов. Определение внутренних сил осуществляется
с помощью так называемого метода сечений, сущность которого заключается в следующем:
1. Мысленно разрезают тело по интересующему сечению.
2. Отбрасывают одну из частей (безразлично, какую).
3. Заменяют действие отброшенной части тела на оставшуюся системой сил, которая в данном случае переходит в разряд внешних. Силы упругости по принципу действия и противодействия всегда взаимны и представляют непрерывно распределенную по сечению систему сил. Их значение и ориентация в каждой точке сечения произвольны, зависят от ориентации сечения относительно тела, величины и направления внешних сил, геометрических размеров тела. Внутренние силы можно привести к главному вектору 
и главному моменту 
. За точку приведения обычно принимают центр тяжести сечения. Выбрав систему координат х, у, z (z – продольная ось по нормали к поперечному сечению, х и у – в плоскости этого сечения) и начало системы в центре тяжести, обозначим проекцию главного вектора на координатные оси через N, Qx, Qy, а проекции главного момента – Мх, Му, Мz. Эти три силы и три момента называют внутренними силовыми факторами в сечении: N – продольная сила, Qx, Qy – поперечные силы, Mz – крутящий момент, Mx, My – изгибающие моменты.
4. Внутренние силы находятся в равновесии с внешними силами, они могут быть определены из уравнений равновесия статики:
(1.1)
Любой внутренний силовой фактор в сечении равен алгебраической сумме соответствующих внешних сил, действующих с одной стороны от сечения.
Внутренний силовой фактор в сечении численно равен интегральной сумме соответствующих элементарных внутренних сил или моментов по всей площади сечения:
(1.1)
Классификация основных видов нагружения связана с внутренним силовым фактором, возникающим в сечении. Так, если в поперечных сечениях возникает только продольная сила N, а другие внутренние силовые факторы обращаются в нуль, то на этом участке имеет место растяжение или сжатие, в зависимости от направления силы N. Нагружение, когда в поперечном сечении возникает только поперечная сила Q, называют сдвигом.
Если в поперечном сечении возникает только крутящий момент М к (Мz), то стержень работает на кручение. В случае, когда от внешних сил, приложенных к стержню, возникает только изгибающий момент Мх (или Му), то такой вид нагружения называют чистым изгибом. Если в поперечном сечении наряду с изгибающим моментом (например, Мх) возникает поперечная сила Qy, то такой вид нагружения называют плоским поперечным изгибом (в плоскости yz). Вид нагружения, когда в поперечном сечении стержня возникают только изгибающие моменты Мх и Му, называют косым изгибом (плоским или пространственным). При действии в поперечном сечении нормальной силы N и изгибающих моментов Мх и Му возникает нагружение, называемое сложным изгибом с растяжением (сжатием) или внецентренным растяжением (сжатием). При действии в сечении изгибающего момента и крутящего момента возникает изгиб с кручением.
Общим случаем нагружения называют случай, когда в поперечном сечении возникают все шесть внутренних силовых факторов.
К особым видам нагружения следует отнести смятие, когда деформация носит местный характер, не распространяясь на все тело, и продольный изгиб (частный случай общего явления потери устойчивости).
1.3. Понятие о напряжениях
Величина внутренних силовых факторов не отражает интенсивности напряженного состояния тела, близости к опасному состоянию (разрушению). Для оценки интенсивности внутренних сил вводится критерий (числовая мера), называемый напряжением. Если в поперечном сечении А некоторого тела выделим элементарную площадку D А (рис. 1.1), в пределах которой выявлена внутренняя сила D R, то за среднее напряжение на площадке D А может быть принято отношение
. (1.3)
Истинное напряжение в точке можно определить, уменьшая площадку:
. (1.4)
Векторная величина 
представляет собой полное напряжение
в точке. Размерность напряжения принимается в Па (Паскаль) или МПа (Мегапаскаль). Полное напряжение обычно в расчетах не применяется, а определяется его нормальная к сечению – составляющая s – нормальное напряжение, и касательные t¢, t² – касательные напряжения (рис. 1.2). Полные напряжения, приходящиеся на единицу площади, можно выразить через нормальные и касательные напряжения:
. (1.5)
Между действующими напряжениями и внутренними силовыми факторами существует следующая связь:
Нормальные и касательные напряжения являются функцией внутренних силовых факторов и геометрических характеристик сечения. Эти напряжения, вычисленные по соответствующим формулам, можно назвать фактическими, или рабочими.
Наибольшее значение фактических напряжений ограничено предельным напряжением, при котором материал разрушается или появляются недопустимые пластические деформации. Первая из этих границ существует у любого хрупкого материала
и называется пределом прочности (s b, t b), вторая имеет место только у пластичных материалов и называется пределом текучести (sт, tт). При действии циклически изменяющихся напряжений разрушение происходит при достижении так называемого предела выносливости (s R, t R), значительно меньшего, чем соответствующие пределы прочности.
1.4. Деформации и перемещения
При воздействии внешних сил тело деформируется, изменяя свои размеры и форму. С физической точки зрения деформации могут быть упругими, пластическими и вязкими.
Упругими называются деформации, возникающие сразу
и полностью после приложения нагрузки и сразу же и полностью исчезающие после ее снятия.
Пластическими (остаточными) называются деформации,
не исчезающие ни сразу после снятия нагрузки, ни по истечении достаточно большого времени.
Вязкими называются деформации, развивающиеся в теле с течением времени, без изменения нагрузки.
В курсе сопротивления материалов объектом изучения является, в основном, упругая деформация.
В геометрическом смысле любая деформация может быть представлена как совокупность линейных (e) и угловых (g) деформаций (рис. 1.3).
, (1.7)
, (1.8)
где e – относительная линейная деформация в продольном направлении, g – угловая деформация (угол сдвига).
Накопление деформаций в связанных друг с другом элементах твердого тела приводит к изменению их первоначального положения в пространстве. Эти изменения называются перемещениями. Перемещение может быть линейным и угловым. Линейным перемещением, например, является прогиб балки
в каком-либо сечении, угловым перемещением – поворот сечения при изгибе и кручении.
Поскольку перемещения – следствие накопления деформаций в элементах тела, они должны быть интегральными функциями внутренних силовых факторов.
Понятия «перемещение» и «деформация» не следует смешивать. Можно привести много примеров, когда деформация есть, а перемещения нет, и наоборот: при отсутствии деформаций имеет место перемещение.
1.5. Основные гипотезы предмета сопротивления
материалов
В теории сопротивления материалов принимают некоторые гипотезы применительно к структуре и свойствам материалов,
а также о характере деформаций.
1. Гипотеза о сплошности материала. Принимается инженерная модель материала, по которой предполагается, что материал сплошь заполняет форму тела.
2. Гипотеза об однородности и изотропности. Материал предполагается однородным и изотропным, т.е. в любом объеме
и в любом направлении свойства материала считаются одинаковыми. В некоторых случаях предположение об изотропности неприемлемо. Например, к анизотропным материалам относятся древесина, бетон, некоторые композиционные материалы.
3. Гипотеза о малости деформаций. Предполагается, что деформации малы по сравнению с размерами тела. Это позволяет в большинстве случае пренебречь изменениями в расположении внешних сил относительно отдельных частей тела и составить уравнения статики для не деформированного тела. В некоторых случаях этот принцип не применим. Такие варианты оговариваются особо.
4. Гипотеза об идеальной упругости. Все тела предполагаются абсолютно упругими. Отклонения от идеальной упругости, которые всегда наблюдаются при нагружении реальных тел, несущественны, и ими пренебрегают до определенных пределов деформирования.
5. Принцип независимости действия сил. Результат воздействия на конструкцию системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности. Этот принцип применим в тех случаях, когда могут быть использованы закон Гука и предпосылка о малости деформации.
6. Гипотеза плоских сечений (гипотеза Бернулли). Поперечные сечения бруса, плоские до приложения к нему нагрузки, остаются плоскими и при действии нагрузки.
1.6. Связь между деформациями и напряжениями.
Закон Гука
Физическая индивидуальность твердых тел с точки зрения сопротивления материалов заключается в том, что для каждого из них связь между внешними силами и вызываемыми ими перемещениями различна.
Впервые эту связь установил в 1660 г. Роберт Гук. Тем самым было положено начало науке о сопротивлении материалов.
Для линейного напряженного состояния этот закон в современной трактовке гласит: напряжение прямо пропорционально относительной продольной деформации и зависит от упругих свойств тела:
, (1.9)
где Е – модуль упругости (Па).
Закон Гука справедлив только до напряжения, называемого пределом пропорциональности. Для чистого сдвига закон Гука имеет вид:
, (1.10)
где G – модуль сдвига (Па).
Модуль сдвига связан с модулем продольной упругости:
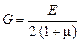. (1.11)
Вопросы для самопроверки
1. Что называется наукой о сопротивлении материалов?
2. Что называется реальным объектом и расчетной схемой?
3. Что подразумевается под схематизацией свойств материала, форм геометрических тел, сил?
4. В чем состоит метод сечения для определения внутренних сил?
5. Раскройте понятия о напряжениях – полном, нормальном, касательном.
6. Раскройте понятие о деформациях и перемещениях, их отличие.
7. Какова связь напряжений с силовыми факторами?
8. Расскажите об основных гипотезах в науке о сопротивлении материалов.
Для лучшего усвоения материала рекомендуется изучить источник [1] (гл. 1, § 1–7).
Глава II. Растяжение и сжатие
2.1. Продольные силы в поперечных сечениях
Растяжением или сжатием называется такой вид нагружения, при котором в поперечных сечениях стержня возникает только один внутренний силовой фактор – продольная сила N.
Продольная сила считается положительной, если она вызывает растяжение (направлена от сечения), и отрицательной, если она вызывает сжатие (направлена к сечению).
В произвольном сечении продольная сила численно равняется алгебраической сумме проекций на ось стержня всех внешних сил, действующих по одну сторону от проведенного сечения.
При этом внешние силы, направленные от сечения, входят
в уравнение со знаком плюс, а направленные к сечению – со знаком минус, что соответствует указанному выше правилу знаков для продольной силы.
. (2.1)
Интегрирование производится по длине участков, на которых действует распределенная нагрузка, а суммирование – по всем участкам, расположенным по одну сторону от исследуемого сечения.
Примером распределенной нагрузки является собственный вес материала стержня. Интенсивность сил тяжести в пределах каждого участка ступенчатого стержня будет величиной постоянной и равной:
, (2.2)
где g – вес единицы объема материала, А – площадь поперечного сечения.
При растяжении-сжатии интенсивность распределенной нагрузки и продольная сила связаны между собой следующей дифференциальной зависимостью:
. (2.3)
Для наглядного представления о характере распределения продольных сил по длине стержня строится эпюра продольных сил.
При построении эпюры следует руководствоваться некоторыми правилами, вытекающими как из метода сечений, так и из дифференциальной зависимости между q и N:
1. Если на участке стержня отсутствует распределенная нагрузка, то продольная сила постоянна.
2. Если на участке имеется равномерно распределенная нагрузка, то продольная сила изменяется по линейному закону.
3. В сечении, где приложена внешняя сосредоточенная сила, эпюра продольных сил имеет скачок на величину этой силы.
4. В концевых сечениях стержня продольные силы равны приложенным в этих сечениях внешним сосредоточенным силам.
2.2. Напряжения, деформации и перемещения
Нормальные напряжения в поперечных сечениях стержня, достаточно удаленных от мест приложения нагрузок, вычисляются по формуле
. (2.4)
Для однородного по длине стержня постоянного сечения при действии продольной силы N нормальные напряжения будут постоянными как по сечению, так и по всей длине. Такое напряженное состояние называется однородным.
При осевом растяжении или сжатии стержня, выполненного из пластичного материала, условие прочности имеет вид
. (2.5)
где smax и N max – нормальное напряжение и продольная сила
в опасном поперечном сечении; [s] – допускаемое напряжение.
Для хрупкого материала условие прочности выглядит следующим образом:
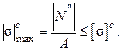(2.6)
Здесь 
и 
– максимальные растягивающее и сжи-
мающее напряжения; 
и 
– допускаемое напряжение на растяжение и допускаемое напряжение на сжатие.
Определяется допускаемое напряжение по формуле
, (2.7)
где sпц – предельное для данного материала напряжение, при котором в материале либо возникают большие пластические деформации, либо происходит разрушение; [ n ] – нормированный коэффициент запаса прочности.
Для материалов, находящихся в пластичном состоянии, за предельное напряжение принимается предел текучести (sт),
а для хрупких материалов – предел прочности (sв), соответственно при растяжении это 
и при сжатии 
.
Таким образом, для пластичных материалов
, (2.8)
где [ n ]= 1,5–2.
Для хрупких материалов
, (2.9)
, (2.10)
где [ n ]= 2,5–3.
Условие прочности позволяет решать три типа задач. Остановимся на них более подробно:
1. Проверка прочности.
По известным продольной силе и размерам поперечного сечения стержня определяют наибольшее напряжение, которое сравнивают с допускаемым, либо определяют фактический запас прочности:
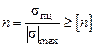, (2.11)
где [ n ] – нормативный коэффициент запаса прочности; n – фактический коэффициент запаса прочности.
Расчет выполняется непосредственно по формулам (2.5) или (2.6).
2. Подбор сечения – проектировочный расчет.
По известным продольной силе и допускаемому напряжению определяется необходимая площадь поперечного сечения стержня:
. (2.12)
3. Определение допускаемой нагрузки.
По известным площади поперечного сечения и материалу (допускаемое напряжение) стержня определяют допускаемое значение продольной силы:
. (2.13)
Затем по известной продольной силе вычисляется допускаемое значение внешней нагрузки.
Размеры нагруженного стержня меняются в зависимости от величины приложенных сил. Так, если до нагружения стержня (рис. 2.1) его длина была равна l, то после нагружения она станет равной l + D l. Величину D l называют абсолютным удлинением стержня.
Мысленно вырежем из стержня бесконечно малый элемент длиной d z. После приложения нагрузки он получит удлинение Dd z. Отношение удлинения к длине элемента
(2.14)
называется продольной линейной деформацией, или линейной деформацией.
В пределах малых удлинений для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность между напряжениями и деформациями:
, (2.15)
где Е – модуль упругости, физическая константа материала.
Если в выражении (2.15) заменить s на 
, а e на 
, то
Абсолютное удлинение стержня на длине l будет равно:
. (2.16)
При постоянных продольной силе и площади поперечного сечения в пределах каждого участка, из выражения (2.16) получаем:
. (2.17)
Изменение поперечных размеров стержня оценивается относительной поперечной деформацией.
Абсолютное уменьшение поперечных размеров
.
Относительная поперечная деформация
,
где d 1и d – конечный и начальный поперечные размеры стержня.
При растяжении e > 0, e¢ < 0, а при сжатии e < 0, e¢ > 0.
Отношение поперечной деформации к продольной, взятой по абсолютной величине при простом растяжении или сжатии, называется коэффициентом Пуассона и обозначается буквой m:
. (2.18)
Для различных материалов значение коэффициента Пуассона колеблется в пределах от 0 до 0,5.
Из формулы (2.15) следует, что продольная деформация 
, тогда 
, или
. (2.19)
При деформации бруса в его материале накапливается потенциальная энергия, величина которой находится по формуле
. (2.20)
Для призматического бруса с постоянной по длине продольной силой выражение имеет вид
.
Удельная потенциальная энергия упругой деформации, т.е. энергия, приходящаяся на единицу объема, будет равна
. (2.21)
2.3. Примеры расчета статически определимых систем
растяжения и сжатия
Пример 1
По оси двухступенчатого стального стержня приложены силы F 1 = 30 кН, F 2 = 70 кН и F 3 = 100 кН (рис. 2.2). Ступени имеют длины l 1 = 25 см, l 2 = 35 см, l 3 = 40 см. Соответствующие площади поперечных сечений: A 1 = 3 см2, A 2 = 4 см2. Модуль упругости для материала стержня Е = 2×105 МПа.
Построить эпюры продольных сил, нормальных напряжений и перемещений.
Решение
1. Построение эпюры N. Разбиваем стержень на три участка, границы которых совпадают с сечениями, где приложены внешние силы. Значения продольной силы на каждом участке определяем, пользуясь методом сечений.
В сечении 1–1 N 1 = F 1 = 30 кН. В сечении 2-2 N 2 = F 1 – F 2 =
= 30 – 70 = –40 кН. В сечении 3-3 N 3 = F 1 – F 2 – F 3 = 30 – 70 + 100 =
= 60 кН.
По полученным значениям строится эпюра продольных сил (см. рис. 2.2).
2. Построение эпюры s. Для вычисления напряжений стержень разбивается на четыре участка. Их границы определяются не только сечениями, где приложены внешние силы, но и сечениями, где меняются поперечные размеры стержня. Пользуясь эпюрой N, находим:
Проверка прочности стержня на наиболее напряженном участке smax = 150 МПа < [s] = 160 МПа.
По полученным результатам строим эпюру нормальных напряжений.
3. Построение эпюры перемещений D.
Определение перемещений начинаем от заделки, где оно равно 0. Перемещение произвольного сечения на расстояние z равно абсолютному удлинению части стержня, которая заключена между этим сечением и заделкой.
Так, перемещение произвольного сечения на третьем участке может быть вычислено по формуле 
.
Это есть уравнение наклонной прямой, так как w ( z )линейно зависит от переменной z при прочих постоянных для данного участка параметрах.
Перемещение сечения D относительно заделки равно абсолютному удлинению участка DE 
Перемещение сечения С относительно заделки складывается из абсолютного укорочения участка CD и удлинения участка DE: 
Аналогично определяем перемещения сечений В и А: 
Эпюра перемещений представлена на рис. 2.2.
Пример 2
Жесткий стержень АС шарнирно закреплен в точке С
и поддерживается стальной тягой ВD круглого поперечного сечения диаметром 20 мм. На части стержня АС приложена равномерно распределенная нагрузка с интенсивностью
q = 80,0 кН/м (рис. 2.3). Допускаемое напряжение для материала тяги ВD [s] = = 160 МПа, модуль упругости Е = 2×105 МПа.
Проверить прочность тяги и определить перемещение свободного конца жесткого бруса, т.е. точки А.
Решение
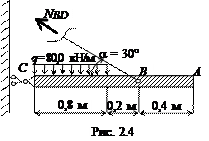1. Определяем усилие, возникающее в тяге ВD под действием приложенной нагрузки. Мысленно рассекаем тягу ВD, действие отброшенной верхней части заменяем внутренним усилием NВD (рис. 2.4). Составляем уравнение равновесия системы в виде суммы моментов действующих на нее сил относительно точки С.
Положительный результат означает, что стержень ВD растягивается.
2. Условие прочности для тяги BD имеет вид:
,
где 
см2.
Тогда 
Оценим перенапряжение в тяге 
. Так как перенапряжение в тяге не превышает 5 %, можно сделать вывод, что прочность тяги BD обеспечена.
3. Для определения перемещения точки А найдем удлинение D l тяги BD и построим план перемещения данной системы, т.е. покажем положение стержневой системы после приложения нагрузки.
Удлинение D l тяги BD равно
План перемещения показан на рис. 2.5.
При построении плана перемещения полагаем, что в точке В тяга не соединяется с жестким стержнем АС. Тогда тяга удлинится на величину D l. Для того чтобы найти новое положение точки В, которая одновременно должна находится на продолжении тяги D l и вместе с жестким стержнем перемещаться по дуге радиусом СВ вниз, надо радиусом DB + D l и радиусом СВ произвести засечки. На основании допущения о том, что перемещения точек тела, обусловленные его упругими деформациями, весьма малы по сравнению с раз-мерами самого тела, заменяем дуги перпендикулярами к соответствующим стержням. Тогда отрезок ВВ 1 будет искомым перемещением точки В, а отрезок АА 1 есть искомое перемещение точки А – D А.
Из прямоугольного треугольника ВВ 1 Е найдем 
мм, из подобия треугольников (D САА 1 ¥ D СВВ 1) получим перемещение точки А.
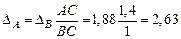мм.
Пример 3
Подобрать из условия прочности поперечные сечения стальных стержней кронштейна, нагруженного силой F = 200 кН,
и определить горизонтальное, вертикальное и полное перемещение узла С (рис. 2.6).
Стержень АС двутаврового поперечного сечения, стержень ВС круглого поперечного сечения. Допускаемое напряжение для материала стержней [s] = 160 МПа, модуль упругости Е = 2×105 МПа.
Решение
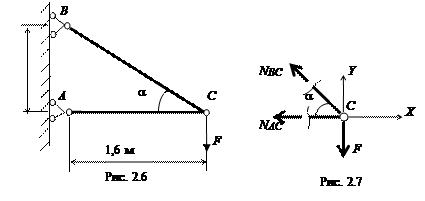
1. Составим уравнения равновесия и определим усилия
в стержнях. Для этого мысленно вырежем узел С. В местах разрезов приложим неизвестные пока усилия в направлении, вызывающем растяжение стержней (рис. 2.7).
Отрицательное значение усилия NАС указывает на то, что стержень испытывает сжатие.
2. Подбираем из условия прочности размеры стержней.
а) для стержня ВС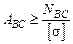 
, причем 
. Тогда 
.
Принимаем в соответствии с таблицей нормальных размеров d = 52 мм. Уточненная площадь стержня ВС 
см2;
б) для стержня АС АAС 
см2.
В соответствии с сортаментом на двутавровые балки по ГОСТ 8239–72 принимаем двутавр № 14 с F = 17,4 см2.
3. Находим изменение длины каждого стержня.
а) удлинение стержня ВС
б) укорочение стержня АС
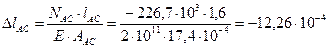м 
мм
4. Определяем перемещение узловой точки С.
План перемещения представлен на рис. 2.8.
Для определения перемещения узла С положим, что стержни в узле С не соединены между собой. Тогда стержень ВС удлинится на величину DlВС,
и стержень АС укоротится на величину D lАС. Новое положение узла С (точка С 1) определится как точка пересечения перпендикуляров к стержням ВС и АС, проведенных из конца стержней ВС + D lВС и АС - D lАС (вместо дуг радиусов ВС + D lВС
и АС - D lАС). Из схемы видно, что горизонтальное перемещение точки С равно DГ = |D lАС | =
= 1,2 мм. Для нахождения второй координаты точки С 1 - D В проведем из точки D перпендикуляр на продолжение стержня ВС. Тогда удлинение D lВС можно представить как разность отрезков 
или 
, откуда
.
Полное перемещение узла С определяется как геометрическая сумма 
мм.
Контрольная работа № 1.
Расчеты на прочность статически определимых систем
растяжения-сжатия
Задача 1. Проверить прочность и определить перемещение свободного конца стержня. Материал стержня – сталь ([s] = 160 МПа, Е = 2×105 МПа). Расчетная схема и числовые данные выбираются в соответствии с шифром по рис. 2.9 и табл. 2.1.
Таблица 2.1
| Номер строки | Цифра шифра | |||||
| схема | а, м | F 1, кН | F 2, кН | F 3, кН | A 1, см2 | |
| 0,30 | ||||||
| 0,35 | ||||||