Лекция №1
Пределы функции
Функция: определение, основные свойства и способы задания
К понятию функции приводит изучение разнообразных явлений в окружающем нас мире. Так, например ясно, что:
1 каждому значению длины куба соответствует его объём;
2 каждому значению радиуса окружности соответствует её длина и площадь круга;
3 каждому показателю рентабельности соответствует определённая величина прибыли.
Во всех этих примерах общим является то, что каждому числовому значению одной величины сопоставляется определённое числовое значение другой.
Эта зависимость между двумя переменными величинами носит взаимный характер, и ни одна из этих величин не играет сама по себе первенствующей роли. Однако в условиях конкретной задачи часто случается так, что заданы значения некоторой величины х (независимой переменной) и по ним определяются соответствующе значения величины y (зависимой переменной).
Независимую переменную величину, то есть величину, для которой мы можем задавать произвольные, интересующие нас значения, называют аргументом. Переменную величину, значения которой зависят от аргумента, называют функцией.
Переменная величина y называется функцией переменной величины х, если каждому значению х, взятому из области её изменения, соответствует по определённому правилу единственное значение y.
Символически функциональная зависимость между переменной y и переменной х записывается с помощью равенства y = f(x), где f обозначает совокупность действий, которые надо произвести над х, чтобы получить y.
Под областью определения (существования) функции f(x) понимается совокупность всех действительных значений аргумента х, при которых функция определена и выражается действительным числом.
|
|
Иногда область определения функции ограничивается физическим или геометрическим смыслом задачи.
Нельзя смешивать область определения функции с областью значений функции.
Область значений функции есть множество всех действительных значений, которые принимает функция.
Способы задания функции.
Имеется несколько способов задания функции.
1 Аналитический способ. Соответствие между х и y задаётся в виде формулы. Например,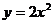 
. Этот способ удобен для выполнения над функцией математических действий, но не всегда нагляден.
2 Табличный способ. Этот способ является наиболее простым. В одной строке (столбце таблицы) записывают все значения аргумента (числа), а во второй строке (столбце) – значения f(x), соответствующие каждому х. Например, через каждые десять дней измеряли диаметр d, мм коробочки хлопчатника. В результате получена следующая таблица.
Таблица № 1 Табличный способ задания функции
| D | ||||||||
| Дни |
Табличный способ удобен для использования, он особенно широко применяется при регистрации результатов опытов, лабораторных анализов и т. д., но представление о функциональной зависимости не является полным.
3 Графический способ. Функция изображается в прямоугольной системе координат в виде графика. Графиком функции y = f(x) называется множество всех точек координатной плоскости с координатами (x, f(x)), то есть таких, координаты которых обращают выражение y = f(x) в тождество.
|
|
Графический способ задания функции очень нагляден, но точность его невелика, поэтому данный способ применяют чаще всего в сочетании с аналитическим и табличным.
Чётные и нечётные функции
Функция y= f(x) называется чётной, если при всех значениях х в области определения этой функции при изменении знака аргумента на противоположный значение функции не изменяется, то есть f(-x) = f(x). Например, парабола 
является чётной функцией, так как 
. График чётной функции симметричен относительно оси Oy.
Функция y= f(x) называется нечётной, если при всех значениях х в области определения этой функции при изменении знака аргумента на противоположный функция изменяется только по знаку, то есть f(-x) = -f(x). Например, функция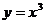 
– нечётная, так как 
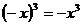. График нечётной функции симметричен относительно начала координат.
Функция, не являющаяся чётной или нечётной, называется функцией общего вида.
Пример. Исследовать на чётность и нечётность функцию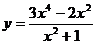 
.
Решение. Подставляем на место аргумента (-х).
– функция чётная.