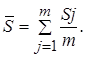
Отклонение суммы рангов, полученных i-тым объектом, от среднего значения рангов равно dj=Sj-S. Тогда коэффициент конкордации, вычисленный по совокупности всех объектов, составит: суммы рангов равно dj=Sj-S. Тогда коэффициент конкордации, вычисленный по совокупности всех объектов, составит:

где n— количество групп равных рангов;
Ti — количество равных рангов в группе.
Величина  рассчитывается при наличии одинаковых рангов.
рассчитывается при наличии одинаковых рангов.
Коэффициент конкордации изменяется в пределах Wє[0; 1].W=1- означает полную согласованность мнений экспертов, W=0 — полную несогласованность. Низкое значение этого коэффициента может быть получено как при отсутствии общности мнений, так и из-за противоположных мнений между подгруппами экспертов, хота внутри подгруппы согласованность может быть высокой.
Для выявления степени согласованности мнений экспертов пользуется коэффициент парной ранговой корреляции

где Ψj=|Ri-Rj+1|, т. е. разность (по модулю) величин рангов оценок i-того направления, назначенных i-тым и (I+1)-тым экспертами.;
Коэффициент парной ранговой корреляции может принимать значения от + 1 до -1. Значение р = 1 соответствует полной согласованности мнений двух экспертов, р =-1 показывает, мнения противоположны.
Для определения уровня значимости коэффициентов W и Pi,j+1 можно использовать критерий
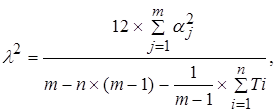
соответствующим таблицам определить уровень значимости полученных результатов. Считается, что групповые оценки экспертов достоверны, если между личными оценками экспертов наблюдается большая согласованность.
Кроме того, количественно степень согласованности мнений экспертов можно определить коэффициентом согласия Е, являвшимся разновидностью коэффициента множественной корреляции. Коэффициент согласия вычисляется по формуле:

где m — число экспертов;
Rij — коэффициент корреляции оценок i и l экспертов.
После вычисления коэффициента согласия он проверяется на значимость, т. е. проверяется гипотеза о случайности получения данного значения Е. Эту гипотезу можно интерпретировать или как независимость оценок экспертов, или как случайность проставления экспертами своих оценок. Проверяется она по процедуре статистической проверки гипотез.
Значение коэффициента согласия и результат его проверки на значимость используются для анализа достоверности групповых оценок при небольшом (m<=15) числе экспертов. При большом количестве экспертов коэффициент согласия обычно уменьшается, и в то же время он оказывается значимым, потому что при их большом числе с большей вероятностью найдется несколько экспертов, мнения которых согласуются, а это приведет к неприятию гипотезы о независимости их мнений. Поэтому при большом числе экспертов для оценки достоверности, наряду с согласованностью, следует использовать понятие устойчивости групповой оценки.
Устойчивость групповых оценок объектов определяется как независимость групповых оценок от состава экспертной группы, т. е. групповая оценка объекта; устойчива, если она не изменяется при исключении некоторого числа экспертов из экспертной группы.
В случаях, когда групповые оценки объекта оказались недостаточными (т. е. коэффициент согласия оказался незначительным или групповые оценки неустойчивы), целесообразно выделить из экспертов некоторую группу, оценки объектов которых, и групповые оценки в рамках группы будут достоверными. В некоторых случаях удается выделить не одну такую группу, а несколько, в каждой из которых оценки экспертов близки. Обычно это случается при проведении экспертиз по сложному вопросу, на решение которого существует несколько точек зрения. Тогда каждая сформированная группа экспертов отражает одну точку зрения, отличную от других.
Следует отметить, что задача группирования экспертов относится к комбинаторным задачам, так что разработать оптимальный алгоритм группирования довольно сложно. Поэтому используются последовательные алгоритмы, суть которых в следующем. Находится пара экспертов, мнения которых наиболее сходны (для этого используется матрица корреляции эксперт — эксперт). Затем из оставшихся m—2 экспертов выделяется эксперт, мнение которого ближе всего к группе из трех экспертов и т. д. На каждом шаге вычисляется коэффициент согласия сформированной группы экспертов и проверяется его значимость. Увеличение группы ведется до тех пор, пока после присоединения к ней нового эксперта групповые оценки объектов остаются достоверны по коэффициенту согласия. После формирования одной группы следует повторить процедуру с оставшимися экспертами, чтобы попытаться сформировать из них еще одну группу.