Лекция № 2
Основы дифференциального исчисления
Производная и дифференциал функции
При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Ёе решение приводит к понятию производной, являющемуся одним из основных понятий математического анализа.
Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена И. Ньютона и Г.В. Лейбница.
Ньютон пришел к открытию дифференциального исчисления при решении задач о скорости движения материальной точки в данный момент времени.
Лейбниц пришел к открытию дифференциального исчисления при решении задач о построении касательной к любой кривой, заданной своим уравнением.
Производной функции y=f(x) в данной точке x называют предел отношения приращения функции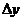 
к соответствующему приращению аргумента 
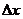при условии, что 
,т.е.
. (1)
Вычисление производной функции по её определению приводит к громоздким преобразованиям, поэтому используют определённые правила и формулы нахождения производных.
Правила дифференцирования
1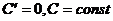 
;
2 
;
3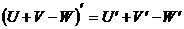 
;
4 
;
5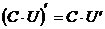 
, 
;
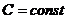6 
;
7 
.
Формулы дифференцирования
1 
2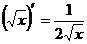 
3 
, 
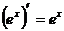
4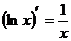 
5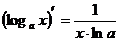 
6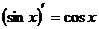 
7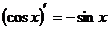 
8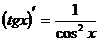 
9 
10 
11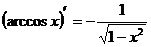 
12 
13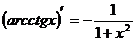 
Геометрическая интерпретация производной впервые была дана в конце 17 века Лейбницем.
Геометрический смысл производной: значение производной функции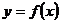 
в точке 
равно угловому коэффициенту касательной, проведенной к графику функции в той же точке x т.е.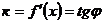 
.
Уравнение касательной: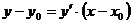 
. (2)
Уравнение нормали: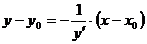 
. (3)
Механическое истолкование производной было дано Ньютоном.
Механический смысл производной: скорость движения материальной точки в данный момент времени равна производной пути по времени, т.е.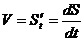 
.
Производную от данной функции часто называют первой производной.
Производной второго порядка называют производную от первой производной. Её обозначение: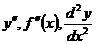 
.
Механический смысл производной второго порядка: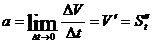 
.
В приложениях математики к решению конкретных задач приходится иметь дело с величинами, числовые значения которых получены путём измерений, и точное их значение неизвестно. Для упрощения и облегчения вычислений в таких случаях используют приближённые методы. Теоретической основой одного из простейших приёмов приближённых вычислений является понятие дифференциала.
Главная часть приращения функции, линейная относительно приращения независимой переменной, называется дифференциалом функции и обозначается знаком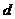 
, т.е. 
.
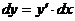Геометрический смысл дифференциала: дифференциал функции y=f(x) геометрически изображается приращением ординаты касательной, проведённой в точке с координатами (x,y) при данных значениях х и Δх.
Для приближённых вычислений величин используют формулу f(x0+∆x)≈f(x0)+f’(x0) ∆x.
С помощью производной, учитывая её механический смысл (скорость изменения некоторого процесса) и геометрический смысл (угловой коэффициент касательной) возможно подробное исследование функций и построение их графиков.
При построении графиков функций с помощью производной пользуются планом:
1 Найти область определения функции и определить точки разрыва, если они имеются.
2 Выяснить является ли функция четной или нечетной, проверить ее на периодичность.
3 Определить точки пересечения графика функции с координатными осями, если это возможно.
4 Найти критические точки функции I рода. (Критические точки I рода – это точки, в которых производная равна нулю или не существует).
5 Определить промежутки монотонности и экстремумы функции.