Производная сложной функции

Сложная функция записывается в виде: где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция 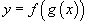также дифференцируема по x и ее производная равна 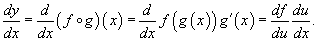Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга. Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции.

5. Вычисление производных функций Пример №1.Найти производную функции

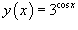Решение. Поскольку то по правилу производной сложной функции получаем

Пример №2.Найти производную функции 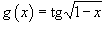. Решение. Здесь мы имеем дело с композицией трех функций. Производная тангенса равна . Тогда

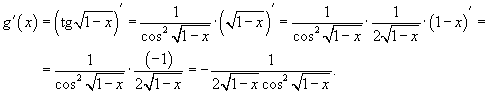
Пример №3.Определить производную функции 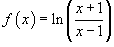. Решение. Применим формулы производной сложной функции и производной частного.

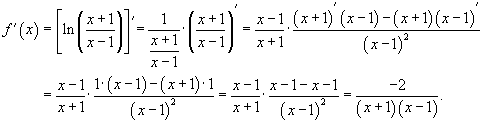
Пример №4.Продифференцировать функцию . Решение. Сначала найдем производную произведения: 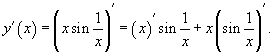Далее, по формуле производной сложной функции

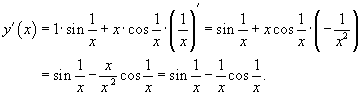
Пример №5.Продифференцировать . Решение. Здесь мы опять имеем дело с «трехслойной» функцией. Поэтому дважды применяем формулу производной сложной функции. Получаем

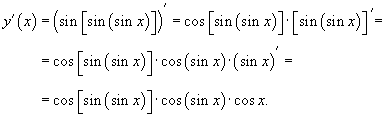
Пример №6. Найдите производные следующих функций:

а) y = sin² 3x

Т.к. данная функция сложная, то используем правило дифференцирования сложной функции y_x´= y_u´u_x´.

Порядок следования функций таков: y = u²; u = sinv; v = 3x

Значит y´ = (u²)´u_v´v´ = 2sin3x(sin3x)´(3x)´= 2sin3xcos3x3 = 3sin6x.

б) y = (x²+3x)⁵

y_x´ =y_u´u_x´= 5(х²+3х)⁴(х²+3х)´= 5(х²+3х)⁴(2х+3).

в) y = ln sin³5x

y´= (ln sin³5x)´(sin³5x)´(sin5x)´

Пример № 7. Найдите производную функции и вычислите .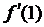

Решение.

Пользуясь правилами дифференцирования, найдем производную:

Вычислим .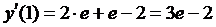

Пример № 8.

Найти производную функции 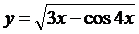и вычислить y’(.

Решение.

y’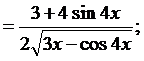

.

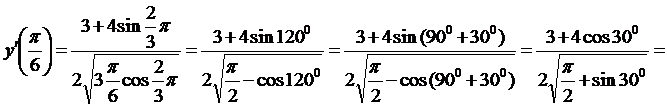
Пример № 8. Вычислить приближенное значение функции y = x³ - 3x² + 30 при изменении аргумента от 3 до 3,002.

Решение.

При небольших изменениях аргумента (здесь приращение аргумента ∆x = 3,002-3 = 0,002 небольшое) можно воспользоваться формулой приближенного значения функции f(x₀+∆x)≈f(x₀)+f’(x₀) ∆x Примем f(x) = y = x³-3x² +30, тогда f’(x) = 3x²-6x, положим x₀ = 3, ∆x = 0,002. Вычислим f(x) = 3³-3∙3²+30 = 30; f’(3) = 3∙3²-6∙3 = 9. Тогда, по формуле будем иметь f(3,002) ≈30+9∙0,002 = 30+0,018 = 30,018.

Решение прикладных задач с помощью производных

Задача №1.

Найти угловой коэффициент касательной, проведенной к кривой y = x³ в точке С (-2;-8).

Решение.

Найдем производную функции y = x³ в точке х = -2. Тогда у` = 3х<sup>2</sup>, у`(-2) = 3∙(-2)² = 12.

Задача №2.

Кривая задана уравнением у = х² +5х. Определить углы наклона касательных к положительному направлению оси ОХ, проведенных к кривой в точке с абсциссой х = -2.

Решение.

Найдем производную, обозначив угол наклона касательной в точке с абсциссой х = -2 через α, получим tg α = y´_x=-2 = 2(-2)+5 = 1, α = arctg 1 = π/4 = 45⁰.

Задача №3.

В какой точке касательная к кривой y = x²-1 параллельна оси ОХ.

Решение.

Так как прямая параллельна оси ОХ, то она образует с ней угол 0⁰ и её угловой коэффициент, равный тангенсу этого угла, равен нулю.

Задача №4.

Тело движется прямолинейно по закону s(t) = 3t³ - 4t + 2. Найти скорость и ускорение в момент времени t = 3.

Решение.

Если известен закон движения как функция времени, то скорость и ускорение – это соответственно первая и вторая производные по времени, то есть

υ = s’(t) = 9t² - 4, тогда υ _t=3 = s’(3)= 9∙3² – 4 = 77 .

а = s’’(t) = 18t, a _t=3 = s’’(3) = 18∙3= 54 .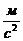

Ответ: 77 и 54 .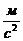

Задача №5.

Исследуйте функцию 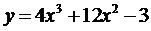на экстремум.

Решение.

Найдем производную, приравняем ее к нулю и решим полученное уравнение:

y’=12x² + 24

12х² + 24х = 0

12х(х + 2) = 0

х = 0 или х = -2.

Воспользуемся достаточными признаками экстремума и проверим меняет ли знак первая производная при переходе через критические точки от меньших значений к большим. Здесь первая производная существует при любых значениях x.

Оценим знаки производной при x = 3, x = -1, x = 1

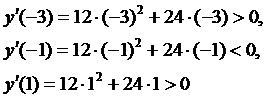
Итак, при переходе слева направо через критическую точку x = -2производная меняет знак с “+” на “–“, то есть функция слева возрастает, а справа убывает. Значит, x = -2 – точка максимума функции. Найдем ее ординату в этой точке:

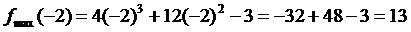
При переходе слева направо через критическую точку x=0 производная меняет знак с “+” на “-”, следовательно, слева убывает справа возрастает, то есть для нее x = 0 – точка минимума, причем .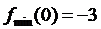

Ответ: Экстремумы данной функции: , .

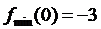Задача №6.

Найдите наибольшее и наименьшее значения функции y = x² - x³ на отрезке [-1;3].

Решение.

Исследуем функцию на экстремум. Если точки экстремума принадлежат данному отрезку, то вычисляем значения функции в точках экстремума и на концах отрезка и выбираем из них наибольшее и наименьшее

y’=2x - 3x²;

2x - 3x² = 0; x(2 - 3x) = 0.

х₁ = 0; x₂ = – критические точки, причем обе принадлежат отрезку [-1;3].

Вычислим значения функции:

f(0) = 0, f(-1) = 2, f(3) = -18, f(2/3) = 19/27

Ответ: f_наиб.=2, f_наим.= -18.

Задача №7.

Найдите точки перегиба графика функции

.

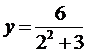Решение.

Для нахождения точек перегиба надо найти вторую производную данной функции, приравнять ее к нулю и решить полученное уравнение. Корни этого уравнения – это критические точки второго рода или точки возможного перегиба. Найдем первую производную:

Теперь найдем вторую производную:

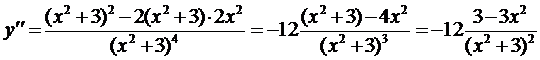
Приравнивая вторую производную к нулю, получим уравнение:

3 - 3x² = 0

1 - x² = 0

откуда x_1,2 = ±1 – критические точки второго рода

Проверим, действительно ли точки x = ±1 являются точками перегиба.

Поскольку для данной функции:

,

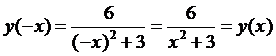то функция четная, значит, если x = 1 – точка перегиба, то x = -1 – тоже точка перегиба. Проверим, меняет ли знак вторая производная при переходе через точку x = 1. Возьмем, например, x = 0 (-1<0<1) и подставим во вторую производную.

Получим .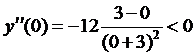

Возьмем теперь x = 2, (2>1), тогда

,

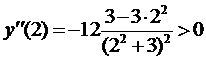(вычислять не обязательно, достаточно правильно оценить знак).

Поскольку вторая производная меняет знак при переходе через точку x =1, то эта точка есть точка перегиба, но тогда и точка x = -1 – тоже точка перегиба.

Ордината обеих точек перегиба будет

,

поскольку точки перегиба лежат на самой кривой.

Итак, точки N₁(-1;1,5), N₂(1;1,5) – точки перегиба графика данной функции

Ответ: N₁(-1;1,5), N₂(1;1,5) – точки перегиба.

Задача №8.

Постройте график функции

.

Решение.

Эскизное построение графика можно выполнить по общепринятой в анализе схеме.

1 Найдем область определения функции: x ε(-∞,0) U (0, ∞); x = 0 – точка бесконечного разрыва, а прямая x = 0 – вертикальная асимптота кривой.

2 Исследуем функцию на четность (нечетность). Вместо x положим –x

Получим:

,

Это признак нечетности функции. Следовательно, ее график центрально симметричен относительно начала координат. Поэтому его можно построить для положительных x и симметрично относительно начала координат перенести для отрицательных x.

3 Найдем точки пересечения графика с осями координат, так называемые “нули” функции. Здесь x ≠ 0, т.к. x = 0 не входит в область определения, значит, с осью O y график не пересекается. Пусть y = 0, тогда .

Это равенство невозможно, так как при любых значения x. Значит, с осью O y график тоже не пересекается.

4 Найдем точки экстремума и нанесем их на график.

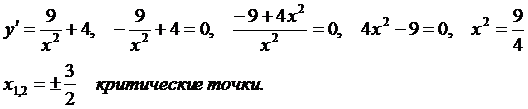
Исследуем характер экстремума в точке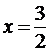

Оценим знаки производной при x=1 и x=2:

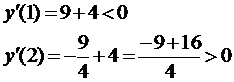, таким образом 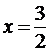- абсцисса точки минимума.

Найдем ординату минимума

Итак, – точка минимума.

Но тогда, в силу центральной симметрии, точка - точка максимума.

5 Интервалы монотонности функции

функция возрастает, если ;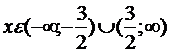

функция убывает, если .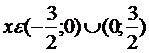

6 Найдем точки перегиба и интервалы выпуклости и вогнутости графика функции 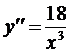ни при каких значениях x вторая производная не обращается в нуль, а в точке разрыва x=0 функция не определена. Следовательно, график не имеет точек перегиба.

Поскольку при x>0 y’’>0, то для x ε(0;∞) кривая вогнутая, а для x ε(-∞;0) (в силу симметрии) – выпуклая.

7.По итогам исследования строим график заданной функции. (Рисунок 1).

Рисунок 1– График функции y =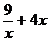

Вопросы для повторения

1 Дайте определение производной функции, приведите обозначения производной.

2 В чём состоит геометрический смысл производной?

3 В чём состоит механический смысл производной?

4 Сформулируйте правила дифференцирования производных.

5 Сформулируйте формулы дифференцирования производных.

6 Дайте определение дифференциала функции.

7 Дайте определении производной второго порядка и укажите её геометрический смысл.

8 Напишите формулу приближённого вычисления значения функции с помощью дифференциала.

9 Сформулируйте признаки возрастания (убывания) функции на интервале.

10 Дайте определение максимума и минимума функции.

11 Сформулируйте общее правило исследования функции на экстремум.

12 Дайте определение точек перегиба функции.

13 Сформулируйте общее правило исследования функции на наличие точек перегиба.

14 Расскажите план исследования функции на построение её графика.