Определение. Многогранник называется правильным, если: 1) он выпуклый; 2) все его грани – равные друг другу правильные многоугольники; 3) в каждой его вершине сходится одинаковое число ребер; 4) все его двугранные равны.
Примером правильного многогранника является куб: он является выпуклым многогранником, все его грани – равные квадраты, в каждой вершине сходятся три ребра, и все двугранные углы куба прямые. Правильный тетраэдр также является правильным многогранником.
Возникает вопрос: сколько существует различных типов правильных многогранников?
Пять типов правильных многогранников.
Рассмотрим произвольный правильный многогранник М, у которого В вершин, Р ребер и Г граней. По теореме Эйлера для этого многогранника выполняется равенство:
В - Р + Г = 2. (1)
Пусть каждая грань данного многогранника содержит m ребер (сторон), и в каждой вершине сходятся n ребер. Очевидно,
 m
m 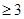 , n
, n 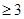 . (2)
. (2)
Так как у многогранника В вершин, и каждой из которых сходятся n ребер, то получаем n  ребер. Но любое ребро соединяет две вершины многогранника, поэтому в произведение n
ребер. Но любое ребро соединяет две вершины многогранника, поэтому в произведение n  каждое ребро войдет дважды. Значит у многогранника имеется
каждое ребро войдет дважды. Значит у многогранника имеется 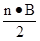 различных ребер. Тогда
различных ребер. Тогда
 = Р
= Р  В =
В = 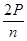 . (3)
. (3)
Далее, в каждой грани многогранника М содержится m ребер, а число граней равно Г. Так как каждое ребро принадлежит двум смежным граням, то число различных ребер многогранника равно  . Тогда
. Тогда
 =Р
=Р  Г=
Г=  . (4)
. (4)
Из (1), (3), (4) получаем 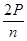 - Р +
- Р +  = 2, откуда
= 2, откуда
 +
+ 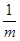 =
=  +
+ 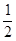 >
> 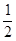 . (5)
. (5)
Таким образом, имеем

Из неравенств 3  и 3
и 3 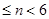 следует, что гранями правильного многогранника могут быть либо правильные треугольники, либо правильные четырехугольники, либо правильные пятиугольники. Причем в случаях m = n = 4; m = 4, n = 5; m = 5, n = 4; m = n = 5 приходим к противоречию с условием
следует, что гранями правильного многогранника могут быть либо правильные треугольники, либо правильные четырехугольники, либо правильные пятиугольники. Причем в случаях m = n = 4; m = 4, n = 5; m = 5, n = 4; m = n = 5 приходим к противоречию с условием  . Поэтому остаются возможными пять случаев: 1) m = n = 3; 2) m = 4, n = 3; 3) m = 3, n = 4; 4) m = 5, n = 3; 5) m = 3, n = 5.
. Поэтому остаются возможными пять случаев: 1) m = n = 3; 2) m = 4, n = 3; 3) m = 3, n = 4; 4) m = 5, n = 3; 5) m = 3, n = 5.
Рассмотрим каждый из этих случаев, используя соотношения (5), (4) и (3).
1) m = n = 3 (каждая грань многогранника – правильный треугольник. Это – известный нам правильный тетраэдр («тетраэдр » означает четырехгранник). 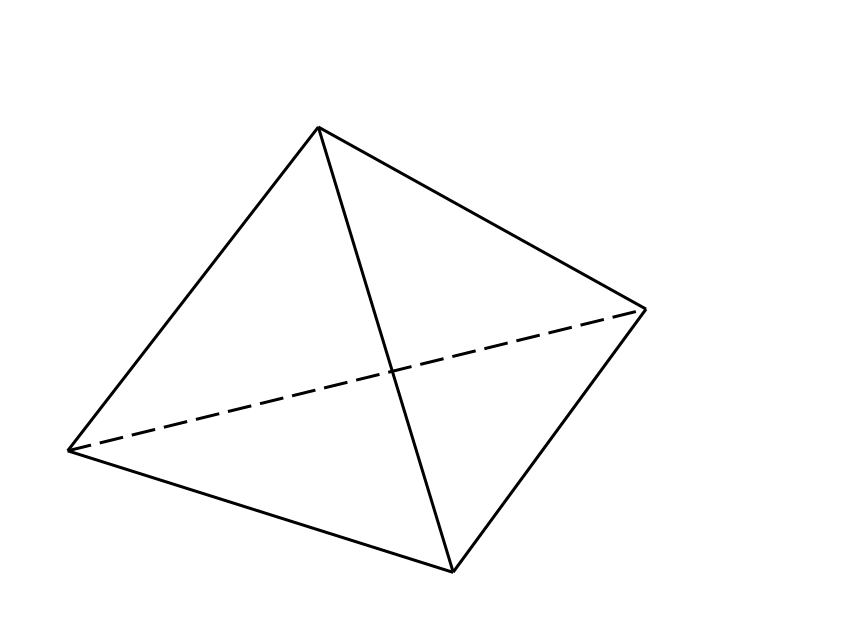
2) m = 4, n = 3 (каждая грань квадрат, и в каждой вершине сходятся три ребра). Имеем
 Р = 12; В =
Р = 12; В =  8; Г =
8; Г =  6.
6.
Получаем правильный шестигранник, у которого каждая грань – квадрат. Этот многогранник называется правильным гексаэдром и является кубом («гексаэдр» -- шестигранник), любой параллелепипед – гексаэдр.
 3) m = 3, n = 4 (каждая грань –правильный треугольник, в каждой вершине сходятся четыре ребра). Имеем
3) m = 3, n = 4 (каждая грань –правильный треугольник, в каждой вершине сходятся четыре ребра). Имеем
 Р = 12; В =
Р = 12; В =  =6; Г =
=6; Г =  =8.
=8.
Получаем правильный восьмигранник, у которого каждая грань – правильный треугольник. Этот многогранник называется правильным октаэдром («октаэдр» -- восьмигранник).
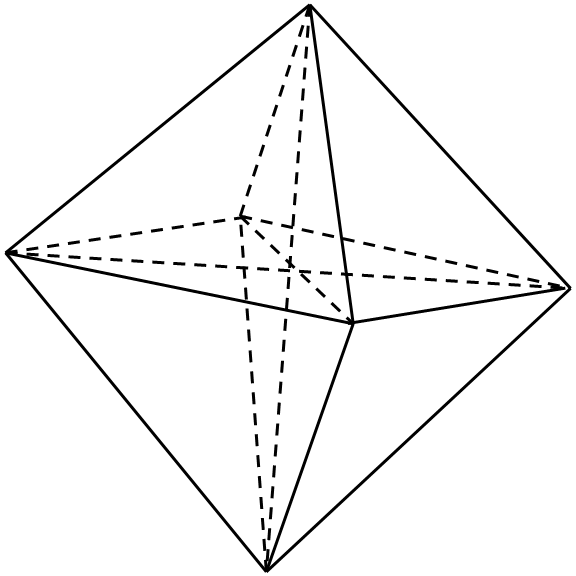
4) m = 5, n = 3 (каждая грань – правильный пятиугольник, в каждой вершине сходятся три ребра). Имеем:
 Р = 30; В =
Р = 30; В =  = 20; Г =
= 20; Г = 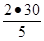 = 12.
= 12.
Получаем правильный двенадцатигранник, у которого каждая грань – правильный пятиугольник. Этот многогранник называется правильным додекаэдром («додекаэдр » -- двенадцатигранник).

5) m = 3,n = 5 (каждая грань – правильный треугольник, в каждой вершине сходятся пять ребер). Имеем
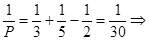 Р = 30; В =
Р = 30; В = 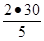 =12; Г =
=12; Г =  = 20.
= 20.
Получаем правильный двадцатигранник. Этот многогранник называется правильным икосаэдром («икосаэдр » - двадцатигранник).
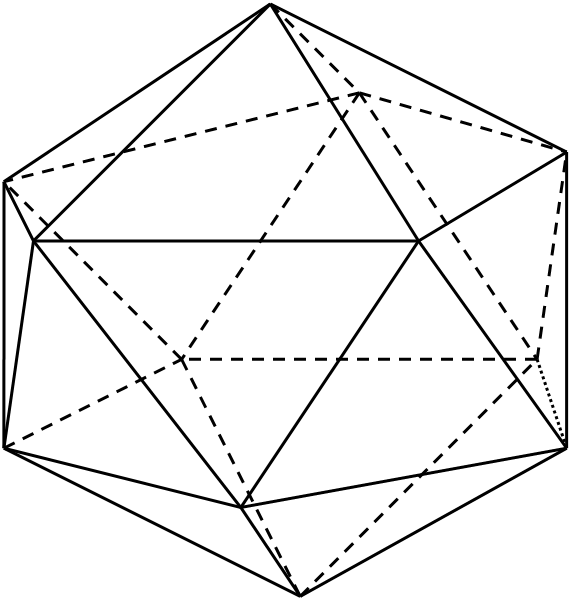
Таким образом, мы получили следующую теорему.
 |
Теорема. Существует пять различных (с точностью до подобия) типов