Проверка устойчивости критерием Михайлова
1 Формулировка критерия Михайлова: Чтобы характеристический полином не имел корней в правой полуплоскости необходимо и достаточно, чтобы полное приращение фазы 
, при изменении частоты от 0 до 
было равно 
, где n – порядок систем.
2 Формулировка критерия Михайлова: Чтобы система была устойчива, необходимо и достаточно, чтобы при изменении частоты от 0 до ∞, годограф Михайлова должен последовательно проходить N – квадрантов и в N-том уходить в бесконечность.
3 Формулировка критерия Михайлова: Чтобы система была устойчива, необходимо и достаточно чередование нулей мнимой (сначала) и действительной части характеристического уравнения при изменении частоты 
от 0 до 
.
Рассчитаем устойчивость нашей системы методом Михайлова:
Запишем характеристический полином системы:
.
Перейдем к комплексным переменным:
Выделим действительную и мнимую части:
Чтобы система была устойчива за Михайловым, нужно чтобы частоты росли а нули чередовались, т.е. было истинно следующее выражение:
Как видим из данной записи, наша система устойчива.
5.3 Предельный коэффициент усиления
Предельный коэффициент усиления системы – эт`о такой коэффициент усиления, при котором система находиться на границе устойчивости – т.е. переходной процесс, характеризующий систему, имеет вид колебательной кривой.
Характеристический полином:
D(s) = 
Чтобы система была устойчива, необходимо и достаточно, чтобы
Из этого следует, что система устойчива при любых k.
6. Анализ качества системы
Под качеством САУ понимают показатели качества переходного процесса и ошибку в установившемся состоянии. К показателям качества переходного процесса относятся:
- время установления tуст – это промежуток времени, за который переходной процесс впервые достигает установившегося значения;
- время регулирования tп.п (переходного процесса) – время, за которое переходная характеристика становится и остается по абсолютной величине меньше наперед заданной величины перерегулирования s.
Рисунок 7.1 - График показателей качества
находим:
hmax=1,22; hуст=0.907; tуст=3,41; tпп=13,6;
Вычислим перерегулирование:
.
7. Вычисление установившейся ошибки
Точность САУ определяется видом входного воздействия, параметрами и структурой системы. Ошибку системы в установившемся режиме можно вычислить, используя передаточную функцию по ошибке.
.
Передаточная функция по ошибке:
.
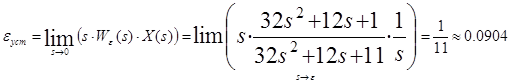
Коэффициенты ошибок:
Методы повышения точности
К числу общих методов повышения точности систем автоматического регулирования относятся:
1) увеличение коэффициента разомкнутой системы;
Рисунок 9.1 – Схема системы с увеличенным коефициентом усиления разомкнутой системы.
Рисунок 9.2 – Ошибка системы после использования 1го метода повышения точности
.
Передаточная функция по ошибке:
.
2) включение в систему изодромного звена;
Рисунок 9.3 – Схема системы с использованием изодромного звена.
Рисунок 9.4 – Ошибка системы после использования 2го метода повышения точности
Передаточная функция изодромного звена имеет вид:
.
Передаточная функция по ошибке:
.
3) ПИД регулятор:
Рисунок 9.5 – Схема системы с использования ПИД регулятора
Рисунок 9.6 – Ошибка системы после использования 3го метода повышения точности
9. Синтез САУ с применением последовательного корректирующего звена
Задача синтеза последовательного корректирующего устройства (ПКУ) заключается в следующем. Имеется исходная система автоматического управления, структура и параметры элементов которой известны. Требуется определить передаточную функцию ПКУ, включение, которого в систему обеспечит получение нужных показателей качества: величины перерегулирования, времени регулирования, ошибки в установившемся режиме.
Алгоритм синтеза последовательного КУ
1) построение ЛАХ исходной разомкнутой системы;
2) построение желаемой ЛАЧХ по заданным показателям качества (время регулирования, запас устойчивости по амплитуде и фазе, степень астатизма, коэффициенты ошибок, коэффициент усиления);
3) определение передаточной функции корректирующего устройства:
На основании приведенного алгоритма синтезируем корректирующее устройство для приведенной выше системы.
Построение исходной ЛАЧХ
1) на частоте 
откладываем значение
L=20*lgK=20*lg10=20
2) определяем частоты сопряжения
:
,
3) через точку 
, 
под наклоном 0 ДБ/декаду, так как в исходной системе нет астатизма (нет свободной s в знаменателе), проводим линию до пересечения с линией 
;
4) так как выражение 
стоит в знаменателе, то дальше кривая пойдет под наклоном –20ДБ/декаду до пересечения с линией 
;
5) выражение 
стоит в знаменателе, поэтому, начиная с частоты и до 
, кривая пойдет под наклоном –40ДБ/декаду.
Построение желаемой ЛАЧХ
Прежде, чем приступить к построению желаемой ЛАЧХ, необходимо задаться желаемыми показателями качества:
- перерегулирование 
;
- время регулирования 
;
- порядок астатизма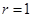 
;
- коэффициент ошибки по скорости 
;
По заданным показателям качества ЛАЧХ строится в такой последовательности:
1) Определяем коэффициент добротности по скорости
Откладываем на оси частот величину 
и через эту точку проводим прямую под наклоном –20ДБ/декаду, так как степень астатизма желаемой системы 
.
2) Определяем частоту среза. Для этого по известному значению 
определяем величину 
, а по величине 
определяем величину
.
Отсюда вычисляем значение частоты положительности
Тогда частота среза выбирается из диапазона 
. В нашем случае
wср=(0,6¸0,9)wп=0,8·wп=0,8·9,425=7,54.
3) Определяем сопрягающие частоты. По зависимости значения перерегулирования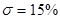 
от запаса устойчивости по модулю определяем значение запаса устойчивости по модулю
Через точку 
проводим линию под наклоном –20ДБ/декаду.
Следующий этап построения – сопряжение частот, которое проводится по типовым наклонам характеристик:
При этом желательно, чтобы в области больших частот желаемая ЛАЧХ была аналогична исходной (ее наклон).
Высокочастотный участок образуется асимптотой с наклоном (-40)дБ/дек, что соответствует наклону исходной ЛАХ в этой области. Это делается для того, чтобы желаемая ЛАХ как можно меньше отличалась от исходной, то есть для упрощения корректирующего устройства.
ЛАХ желаемой системы построена по типовым наклонам 20-40-20-40
Частоты w*1,w*2,w*3,w*4 определяем графически:
w*1=0,125; w*2=1,13; w*3 =30.
Для ЛАХ запишем:
Передаточная функция корректирующего устройства запишется следующим образом:
,
где 
Все построения приведены ниже.
Моделируем систему в среде MatLab:
Рисунок 10.2 – Модель системы в среде MatLab
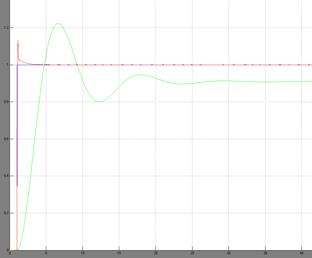
Рисунок 10.3 – Переходной процесс скорректированной системы
Рассмотрим переходные процессы исходной и усовершенствованной систем. Очевидно, что введение ПКУ существенно улучшило показатели качества САУ. Перерегулирование не превышает 13% (хотя в исходной САУ – 22%), время регулирование – 0,25с (в исходной САУ – 13,6с), время установления – 0,1с (в исходной САУ – 3,41с).
Заключение
В данной курсовой работе был рассмотрен пример синтеза системы. Построив функциональную схему системы и проанализировав звенья, вошедшие в её состав, мы получили структурную схему САУ и построили её модель в среде разработки MatLab. В ходе исследования свойств системы, мы рассчитали её устойчивость и проанализировали качество и точность. Для улучшения показателей полученных в результате расчетов качества системы, был применен метод синтеза САУ с применением последовательного корректирующего звена. Это позволило добиться следующих показателей качества скорректированной системы: время переходного процесса уменьшилось с 13,6с до 0,25с, перерегулирование – со значения 22% понизилось до 12%.
Таким образом, можно сделать вывод, что спроектированная в данной работе САУ отвечает требованиям по устойчивости, точности в установившемся режиме и требованиям к качеству переходных процессов.