Выполненные задания присылать на почту alla.kurbatova2014@yandex.ru
Определитель квадратной матрицы. Определители 1-го, 2-го, 3-го порядков.
Определители матриц
Для каждой квадратной матриц вводится важная ее числовая характеристика, называемая определителем этой матрицы. Правило, по которому по элементам данной квадратной матрицы произвольного порядка вычисляется ее определитель, достаточно сложно, поэтому будем вводить это правило «постепенно», повышая порядок определителя. Пока же ограничимся таким неконструктивным определением.
Каждой квадратной матрице можно по некоторому правилу поставить в соответствие число, которое называется определителем данной матрицы. Для определителя квадратной матрицы A, общий вид которой
А = 
применяются различные обозначения. Укажем наиболее употребительные: detA, D, D(А) или развернутое, в котором перечисляются все элементы данной матрицы
. Прямые черты, заменяющие круглые (матричные) скобки, указывают на то, что имеется в виду именно определитель матрицы, т.е. единственное число, а не сама матрица A.
Будем подходить к строгому определению определителя, рассмотрев это правило последовательно для определителей матриц 1 -го, 2 -го и 3 -го порядков.
Определителем матрицы 1-го порядка называется число, равное единственному имеющемуся матричному элементу этой матрицы. Определение настолько простое, что нет необходимости иллюстрировать его примером.
Определитель матрицы 2-го порядка: если А= 
, то
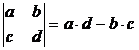
Например, 
.
Рассмотрим определитель матрицы 3-го порядка А = 
.
Для вычисления определителя именно третьего порядка есть упрощенная формула
,
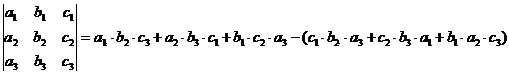которая схематически (для запоминания) записывается так:
 |
– первые три слагаемые (берутся со знаком +)
– последние 3 слагаемые (берутся со знаком −)
Пример. Найдем по упрощенной схеме определитель матрицы (4).
.
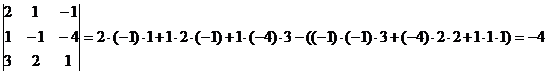!!! Все, что мы будем далее говорить для этой матрицы, справедливо и для квадратной матрицы любого порядка. Определение определителя матрицы содержит два новых понятия. Оказывается, для каждого элемента матрицы (а их 9) можно посчитать 2 числа, которые называются минором и алгебраическим дополнением этого элемента.
Минором элемента матрицы aij (обозначается Мij) называется значение определителя матрицы, получающейся из данной матрицы вычеркиванием строки и столбца, на пересечении которых стоит данный элемент (т.е. вычеркиванием i -ой строки и j -го столбца).
Алгебраическим дополнением элемента матрицы aij (обозначается Аij) называется число, определяемое по формуле
(3) Аij = (–1)i+j Мij.
Поскольку (–1) в целой степени принимает всего два значения (1 – если показатель степени есть четное число и (–1) – если нечетное), то алгебраическое дополнение элемента матрицы либо ничем не отличается от минора этого элемента (если сумма его нижних индексов – т.е. сумма номеров строки и столбца – есть четное число) или отличается от минора только знаком (если сумма нижних индексов нечетна).
Пример. Найти миноры и алгебраические дополнения всех элементов матрицы
(4) А =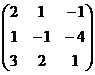 
.
Сначала ищем миноры всех элементов.
М11= 
, М12= 
, М13= 
,
М21=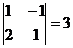 
, М22= 
, М23= 
,
М31=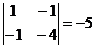 
, М32= 
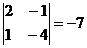, М33= 
.
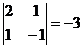Учитывая формулу (3) и приведенные ниже пояснения для этой формулы, получаем следующие алгебраические дополнения
А11=7, А12= –13, А13=5, А21= –3, А22=5, А23= –1, А31= –5, А32=7, А33= –3
Для матрицы (4) для каждой строки (и столбца) проделаем: составим сумму попарных произведений ее (его) элементов на их алгебраические дополнения. Например, для второго столбца: 
. Взяв любой другой столбец (или строку), получим то же самое число (для данной матрицы (– 4)). Это общее свойство всех квадратных матриц − результат таких вычислений не зависит от того, какую строчку или столбец матрицы мы выбрали. Поэтому корректно следующее определение.
Определителем квадратной матрицы (любого порядка!) называется число, равное сумме попарных произведений элементов любой строки (столбца) на их алгебраические дополнения.
Поэтому для матрицы (4) по определению: D = 
.
J Для вычисления определителей матриц более высокого (чем третьего) порядка упрощенной схемы нет, поэтому используется только метод, данный в определении: выбирается строка или столбец матрицы и вычисляется сумма попарных произведений соответствующих элементов матрицы на их алгебраические дополнения. При этом вычисление алгебраических дополнений – самый трудоёмкий этап. Но поскольку строку (или столбец) можно выбирать произвольно (результат от этого не зависит), то проще выбрать ту, среди элементов которой как можно больше нулевых. При этом алгебраические дополнения нулевых элементов можно не считать, так как при составлении упомянутой выше суммы попарных произведений соответствующие слагаемые все равно обратятся в ноль.
Пример. Вычислить определитель 4-го порядка: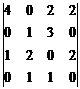 
.
Решение. Самое большое количество нулей в любой из строк или столбцов равно 2. Поэтому для вычисления определителя выбираем любую строку или столбец с двумя нулями. Выберем, например, первый столбец (при этом говорят, что определитель будет разлагаться по первому столбцу):
.
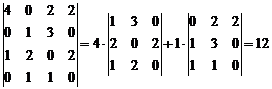Появившиеся два определителя 3-го порядка можно считать по приведенной выше упрощенной схеме.
Если среди элементов матрицы нулей мало (или нет вовсе), то можно специальными действиями привести определитель к такому виду, у которого есть строка (или столбец), в которой отличен от нуля только один элемент. После этого определитель легко вычисляется разложением по этой строке (столбцу). Привести определитель к такому виду помогают свойства определителей, рассмотренные ниже.
Свойства определителей
1. Если у определителя какая-либо строка (столбец) состоит из нулей, то определитель равен нулю.
2. Если какие-либо две строки (два столбца) определителя равны или пропорциональны (т.е. элементы одной строки (столбца) получаются умножением элементов другой строки (столбца) на одно и то же число), то определитель равен нулю.
3. Если две строки (два столбца) поменять местами, то определитель изменит знак.
4. Общий множитель элементов любой строки или столбца можно выносить за знак определителя.
5. Если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), предварительно умноженные на одно и то же число, то определитель не изменится.
Как сказано выше, с помощью этих свойств можно привести определитель к такому виду, у которого есть строка (или столбец), в которой отличен от нуля только один элемент. Для приведения определителя к такому виду необходимо:
Вынести общие множители (если таковые имеются) из строк или столбцов за знак определителя (свойство 4.). Это позволяет уменьшить элементы определителя (что облегчает его дальнейшее вычисление), а также, возможно, получить элементы, равные 1 или (−1), что поможет выполнению следующего пункта.
Выбрать строку (или столбец), в которой есть элемент 1 или (−1) (если такие строки или столбцы есть) и с помощью этого элемента (и последнего свойства определителей) обнулять остальные элементы выбранной строки или столбца.
Иллюстрирует сказанное следующий пример
Пример.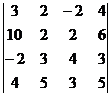 
= {вынесем 2 из второй строки (свойство 4)} =
2 ∙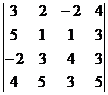 
= {С помощью элемента а22=1 и свойства 5 обнуляем все элементы второй строки, кроме самого а22=1. Для этого а) прибавляем к 1 -му столбцу 2 -ой, умноженный поэлементно на (−5); б) прибавляем к 3 -му столбцу 2 -ой, умноженный на (−1); в) прибавляем к 4 -му столбцу 2 -ой, умноженный на (−3)} = 2 ∙ 
= {раскладываем определитель по второй строке} = 2∙1∙(−1)2+2 ∙ 
= {для облегчения вычисления определителя 3 -го порядка выносим (−1) из первых двух столбцов, а из третьего (−2) }= −4 ∙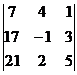 
= {вычисляем определитель третьего порядка по упрощенной схеме}= 440
Домашнее задание
 |  |
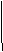1. 
Вычислить определители а) 7 4 б) 9 -3
6 5 7 2
№2. Вычислить определитель
№3. Вычислить определитель
