При решении задач этого раздела нужно знать определения подмножества и основных операций над множествами.
Пример 1. Пусть А = 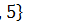 , В =
, В =  . Найти А
. Найти А  В, А
В, А  В, А\В, В\А, А
В, А\В, В\А, А  В.
В.
►По определению операций над множествами получим:
А  В =
В = 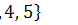 ; А
; А  В ={4}; А\В = {1, 5},
В ={4}; А\В = {1, 5},
В\А = {2};A 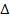 B = {1, 2, 5}. ◄
B = {1, 2, 5}. ◄
Пример 2. Найти все подмножества множества А ={1, 4, 7}.
►Множество всех подмножеств множества А обозначается  ,
,
 = {
= {  , {1}, {4}, {7}, {1, 4}, {1, 7}, {4, 7}, {1, 4, 7}},
, {1}, {4}, {7}, {1, 4}, {1, 7}, {4, 7}, {1, 4, 7}},
 , А – несобственные подмножества А, остальные подмножества - собственные.◄
, А – несобственные подмножества А, остальные подмножества - собственные.◄
Булева алгебра множеств
Основным типом примеров этого пункта является доказать равенство множеств, заданных формулами алгебры множеств. Решение таких примеров следует начинать с построения диаграмм Виенна для левой и правой частей. Если картинки не совпали, то вы уже решили пример и показали, что равенство не имеет места. В противном случае рекомендуется перейти к булевым формулам алгебры множеств и воспользоваться основными равенствами булевой алгебры множеств.
Пример 1. Доказать, что А\(А\В) = А  В,
В,
►Построим диаграммы Виенна левой и правой частей (рис. 1.1).
a) левая часть
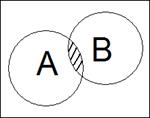
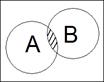
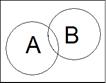
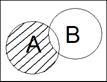
→ →
A\B A\(A\B)
b) правая часть
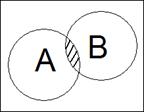
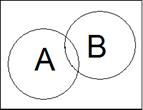
→
А  В
В
Рис.1.1. Диаграммы Виенна
Перейдем к булевым формулам алгебры множеств:
А\(А\В) = А  = А
= А 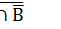 = А
= А  (
( ) = = А
) = = А  (
( В) = (А
В) = (А  )
)  (А
(А  ) =
) =  (А
(А  В) = = А
В) = = А  В◄
В◄
Графы
Во многих задачах теории графов графы удобно описывать матрицами. Выделяют матрицу смежности и матрицу инцидентности.
Пример 1. Для графа G, приведенного на рис. 1.2, найти матрицу смежности A(G) и матрицу инцидентности B(G).
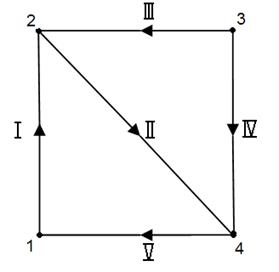
Рис. 1.2. Граф G
►По определению:
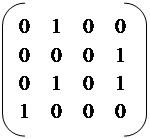
A 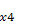 =,
=,
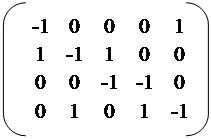 |
B  =.◄
=.◄
Минимизация булевых функций
Минимизация – это упрощение логических выражений путем уменьшения количества операций и символов в формулах, которые реализуют булевые функции. Одной из целей минимизации является упрощение логических устройств и достижение максимальной экономичности разрабатываемых систем.
Для минимизации булевых функций используется ряд методов, среди которых наибольшее применение находят:
1) метод неопределенных коэффициентов;
2) метод Квайна – Мак Класски.
Пример 1. Методом неопределенных коэффициентов минимизировать функцию 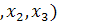 = Y
= Y 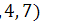 .
.
►Представим функцию в виде ДНФ самого общего вида:
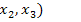 =
= 







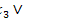


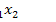



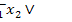

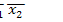





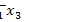


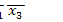
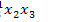

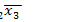

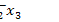

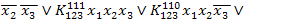
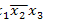
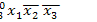

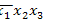

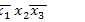
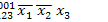


 1
1  2
2  3,
3,
где  ,
,  ,…,
,…,  - неопределённые коэффициенты, принимающие значение 0 или 1 и подбираемые так, чтобы получающаяся после этого ДНФ была минимальной.
- неопределённые коэффициенты, принимающие значение 0 или 1 и подбираемые так, чтобы получающаяся после этого ДНФ была минимальной.
Подставив наборы значений переменных в ДНФ, получим:
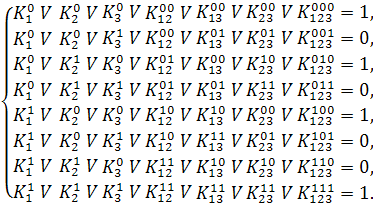
После вычёркивания нулевых коэффициентов имеем:
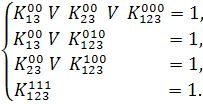
Результат: 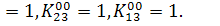
Ответ: 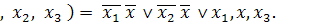
Задания к лабораторным работам
Лабораторная работа №1
Таблицы истинности. Нормальные формы
Цель работы: научиться строить таблицы истинности формул алгебры высказываний, упрощать формулы, находить двойственные формулы и совершенные нормальные формы.
Задания.
Для данной формулы алгебры высказываний:
а) построить таблицу истинности;
б) найти двойственную формулу и построить таблицу истинности двойственной формулы;
в) найти СДНФ и СКНФ по таблице истинности с помощью равносильных преобразований.
1. 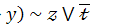
2. 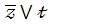
3. 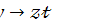
4. 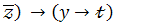
5. 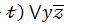
6. 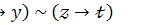
7. 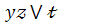
8. 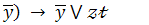
9. 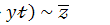
10. 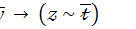
11. 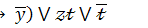
12. 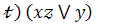
13. 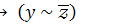
14. 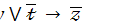
15. 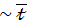
16. 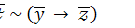
17. 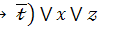
18. 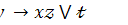
19. 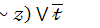
20. 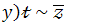
21. 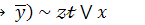
22. 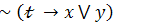
23. 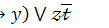
24. 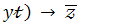
25. 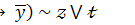
Лабораторная работа №2
Алгебра множеств
Цель работы: освоить основные понятия теории множеств, научиться решать типовые задачи.
Задания.
1) Для данного универсального множества Е и данных множеств А и В найти
А 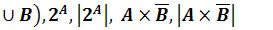 .
.
1. 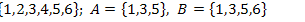
2. 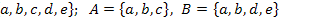
3. 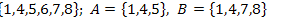
4. 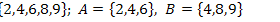
5. 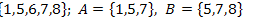
6. 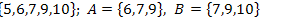
7. 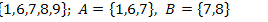
8. 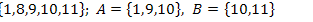
9. 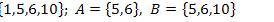
10. 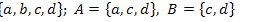
11. 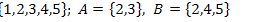
12. 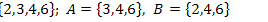
13. 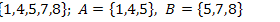
14. 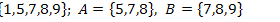
15. 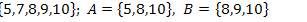
16. 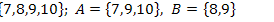
17. 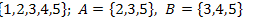
18. 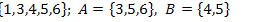
19. 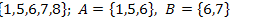
20. 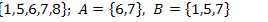
21. 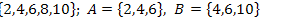
22. 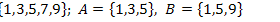
23. 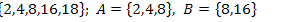
24. 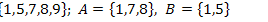
25. 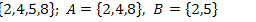
2) Для данного универсального множества
Е и данных множеств А и В найти
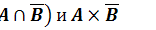 .
.
1. 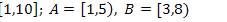
2. 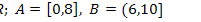
3. 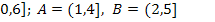
4. 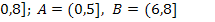
5. 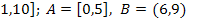
6. 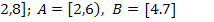
7. 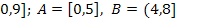
8. 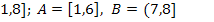
9. 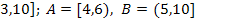
10. 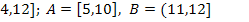
11. 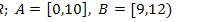
12. 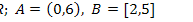
13. 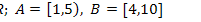
14. 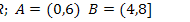
15. 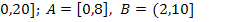
16. 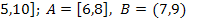
17. 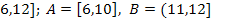
18. 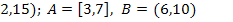
19. 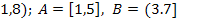
20. 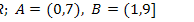
21. 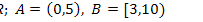
22. 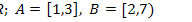
23. 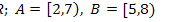
24. 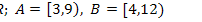
25. 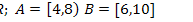
3) Доказать равенства.
1. 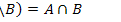
2.  =
= 
3. 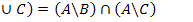
4. 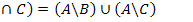
5. 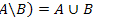
6. 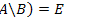
7.  =
= 
8. 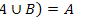
9. 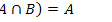
10. 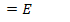
11. 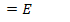
12. 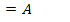
13. 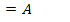
14. 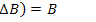
15. 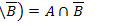
16. 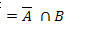
17. 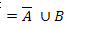
18. 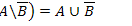
19. 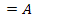
20. 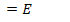
21. 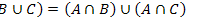
22. 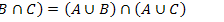
23. 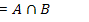
24. 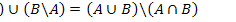
25. 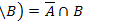
Лабораторная работа №3
Графы и их матрицы
Цель работы: освоить основные понятия теории графов, находить матрицы графов.
Задания.
Для данного графа G(X,U,f) найти:
а) число связности C(G) и число сильной связности SC(G).
б) мосты;
в) хроматическое число X(G);
г) матрицу смежности A(G);
д) матрицу инцидентности B(G).
1. 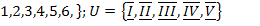 ;
; 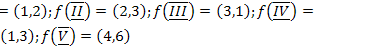
2. 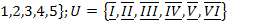 ;
; 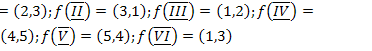
3. 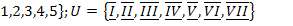 ;
;
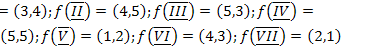
4. 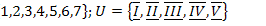 ;
; 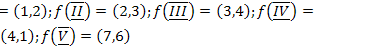
5. 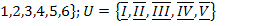 ;
; 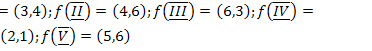
6. 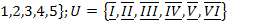 ;
; 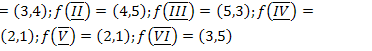
7. 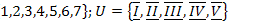 ;
; 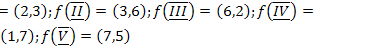
8. 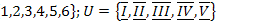 ;
; 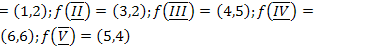
9. 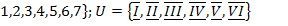 ;
; 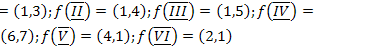
10. 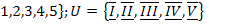 ;
; 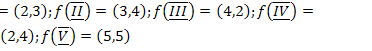
11. 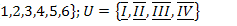 ;
; 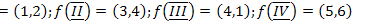
12. 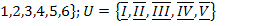 ;
; 
13. 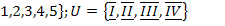 ;
; 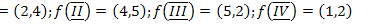
14. 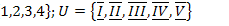 ;
; 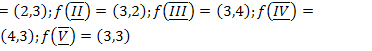
15. 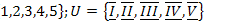 ;
; 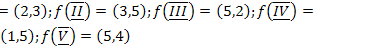
16. 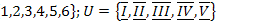 ;
; 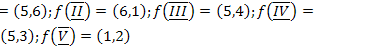
17. 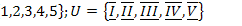 ;
; 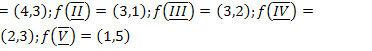
18. 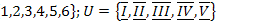 ;
; 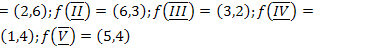
19. 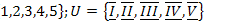 ;
; 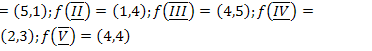
20. 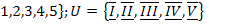 ;
; 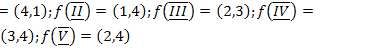
21. 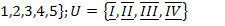 ;
; 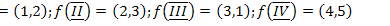
22. 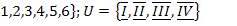 ;
; 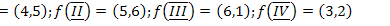
23. 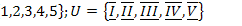 ;
; 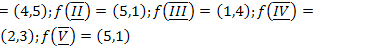
24. 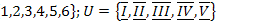 ;
; 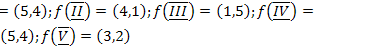
25. 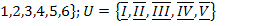 ;
; 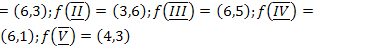
Лабораторная работа №4