Введение
Базовая теплотехническая подготовка студента осуществляется в
процессе изучения общепрофессиональной и специальной дисциплин в
курсах «Теплотехника» и «ТТР в ПТР в л/з производстве», а также
смежных дисциплин.
В результате изучения дисциплины «Теплотехника» студенты
получают представление о процессах горения топлива, теплопередаче и
аэродинамике печных газов как о единой системе, характеризующей
работу установок.
Тепловые установки промышленности эксплуатируются
при высоких температурах. Физические свойства материалов и газов
при воздействии высоких температур изменяются, а в сырьевых
материалах протекают сложные физико-химические процессы. Это
необходимо учитывать при выполнении теплотехнических расчетов
высокотемпературных установок.
Чтобы выбрать оптимальный вариант конструкции и организации
работы проектируемой установки, студент должен, используя
теоретические знания, полученные при изучении дисциплин, показать
владение методиками теплотехнических расчетов: расчета горения
топлива, составления теплового баланса установки,
аэродинамического расчета. Решаются сложные задачи
расчета теплопередачи, происходящей в установках между газами,
материалами и элементами конструкций.
Необходимо также уметь выполнять расчеты технико-экономических
показателей тепловых установок и оценивать полученные результаты.
В методических указаниях приводятся краткие теоретические
положения, которые используются при решении конкретных задач,
справочные данные и варианты индивидуальных заданий.
Основная часть.
Диффу́зия (лат. diffusio — распространение, растекание, рассеивание, взаимодействие) — процесс взаимного проникновения молекул одного вещества между молекулами другого, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму. В некоторых ситуациях одно из веществ уже имеет выравненную концентрацию и говорят о диффузии одного вещества в другом. При этом перенос вещества происходит из области с высокой концентрацией в область с низкой концентрацией (по градиенту концентрации.
|
|
Примером диффузии может служить перемешивание газов (например, распространение запахов) или жидкостей (если в воду капнуть чернил, то жидкость через некоторое время станет равномерно окрашенной). Другой пример связан с твёрдым телом: атомы соприкасающихся металлов перемешиваются на границе соприкосновения. Важную роль диффузия частиц играет в физике плазмы.
Молекулярная диффузия в газах и растворах жидкостей происходит в результате хаотического движения молекул, не связанного с движением потоков жидкости. В этом случае имеет место перенос молекул распределяемого вещества из областей высоких концентраций в область низких концентраций. Кинетика переноса подчиняется в этом случае первому закону Фика, формулировка которого аналогична закону теплопроводности: количество продиффундировавшего вещества пропорционально градиенту концентраций, площади, перпендикулярной направлению диффузионного потока, и времени. Для всей поверхности диффузии S первый закон Фика выразится как:
M=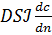 
где ^ D – коэффициент молекулярной диффузии;
S – поверхность, нормальная к направлению диффузии;
|
|
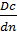– градиент концентрации вещества на единицу длины пути n диффундирующего вещества.
Коэффициент диффузии показывает, какое количество вещества диффундирует через поверхность 1 м2 в течение 1 с при разности концентраций равной единице на расстоянии 1 м.
Знак минус в правой части уравнения показывает, что при молекулярной диффузии в направлении перемещения вещества концентрация убывает.
Молекулярной диффузией называется перенос распределяемого в-ва, обусловленный беспорядочным движением самих молекул. Молекулярная диффузия описывается первым законом Фика, согласно которому кол-во в-ва dМ продиффундировавшего за время dt ч/з элементарную поверхность dF (нормальную к направлению диффузии) пропорционально градиенту концентрации
Коэффициент пропорциональности D в выражении закона Фика называется коэффициентом молекулярной диффузии, или просто коэффициентом диффузии. Знак минус перед правой частью первого закона Фика указывает на то, что молекулярная диффузия всегда протекает в направлении уменьшения концентрации распределяемого компонента.
Пример.
Перейдем к задаче, для которой нам придется несколько изменить метод анализа, — к задаче о диффузии. Предположим, что мы взяли ящик, заполненный газом, находящимся в тепловом равновесии, а потом в любое место внутри ящика вспрыснули небольшое количество другого газа. Назовем первоначальный газ газом «фона», а новый газ — «особым» газом. Особый газ начинает распространяться по всему ящику, но распространение это замедляется наличием молекул фона. Явление такого замедленного распространения называется диффузией. Диффузия в основном определяется столкновениями молекул особого газа с молекулами фона. После многих столкновений особые молекулы более или менее равномерно распределятся по всему ящику. Важно не спутать диффузию газа с переносом больших количеств вещества в результате конвекционных токов. Обычно смешение двух газов происходит именно в результате комбинации конвекции и диффузии. Сейчас нас интересует только такое перемешивание, которое не сопровождается «порывами ветра». Газ распространяется только благодаря молекулярному движению, т. е. происходит диффузия. Давайте выясним, быстро ли происходит диффузия.
|
|
Итак, мы приступаем к вычислению общего потока молекул особого газа, порождаемого молекулярным движением. Общий поток не равен нулю только тогда, когда распределение молекул отличается от равновесного, иначе усреднение молекулярного движения сводит общий поток к нулю. Рассмотрим сначала поток в направлении оси х. Чтобы определить, чему этот поток равен, мы должны вообразить площадку, перпендикулярную к оси, и подсчитать число молекул, пересекающих эту площадку. Чтобы определить общий поток, мы должны считать положительными те молекулы, которые движутся в направлении положительных х, и вычесть из этого числа те молекулы, которые движутся в противоположном направлении. Как мы неоднократно убеждались, число молекул, пересекающих площадку в течение времени ΔT, равно числу молекул, находящихся к началу интервала ΔT внутри объема, заключенного между нашей площадкой и площадкой, расположенной от нее на расстоянии v ΔT. (Заметим, что здесь v — настоящая скорость молекулы, а отнюдь не скорость дрейфа.)
Мы упростим наши выкладки, если возьмем площадку единичной площади. Тогда число особых молекул, пересекающих площадку слева направо (справа от площадки лежат положительные x-направления), равно n_vΔT, где n_ — число особых молекул в единичном объеме слева от площадки (с точностью до множителя ˜ 1/6, но мы такими множителями пренебрежем!). Аналогично, число особых молекул, движущихся справа налево, равно n+vΔT, где n+— плотность особых молекул справа от площадки. Если мы обозначим молекулярный поток буквой J, под которой мы будем понимать общий поток молекул через единичную площадку за единицу времени, то получим
J= 
Схема молекулярной диффузии.
