ПОНИЖЕНИЕ ПОРЯДКА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Метод повторного интегрирования правой части
Дифференциальное уравнение вида y ( n ) = f (x) решается последовательным интегрированием правой части. Причём интегрировать придется ровно n раз.
Пример 1
Найти общее решение дифференциального уравнения y'' = x 2 – 2 x.
Решение: Данное дифференциальное уравнение имеет вид y'' = f (x).
Понижаем степень уравнения до первого порядка:
y' = ∫ (x 2 – 2 x) dx =  x 3 – 2·
x 3 – 2·  x 2 + C 1 =
x 2 + C 1 =  – x 2 + C 1.
– x 2 + C 1.
Теперь интегрируем правую часть еще раз, получая общее решение:
y = ∫ ( – x 2 + C 1) dx =
– x 2 + C 1) dx =  ·
·  –
–  + C 1 x + C 2 =
+ C 1 x + C 2 =  –
–  + C 1 x + C 2.
+ C 1 x + C 2.
Ответ: общее решение: y =  –
–  + C 1 x + C 2.
+ C 1 x + C 2.
Пример 2
Найти частное решение уравнения, соответствующее заданным начальным условиям
y''' = e 2 x ; y (0) =  , y' (0) =
, y' (0) =  , y'' (0) = –
, y'' (0) = –  .
.
Решение: Данное уравнение имеет вид y''' = f (x). Необходимо последовательно три раза проинтегрировать правую часть.
Сначала понижаем степень уравнения до второго порядка:
y'' = ∫ e 2 x dx =  e 2 x + C 1.
e 2 x + C 1.
Первый интеграл принёс нам константу C 1. В уравнениях рассматриваемого типа рационально сразу же применять подходящие начальные условия.
Итак, у нас найдено y'' =  e 2 x + C 1 и, очевидно, к полученному уравнению подходит
e 2 x + C 1 и, очевидно, к полученному уравнению подходит
начальное условие y'' (0) = –  .
.
В соответствии с ним: y'' (0) =  + C 1 = –
+ C 1 = –  => C 1 = –1. Таким образом: y'' =
=> C 1 = –1. Таким образом: y'' =  e 2 x – 1.
e 2 x – 1.
На следующем шаге берём второй интеграл, понижая степень уравнения до первого порядка:
y' = ∫ ( e 2 x – 1) dx =
e 2 x – 1) dx =  e 2 x – x + C 2.
e 2 x – x + C 2.
В соответствии с начальным условием y' (0) =  : y' (0) =
: y' (0) =  – 0 + C 2 =
– 0 + C 2 =  => C 2 = 0.
=> C 2 = 0.
Таким образом: y' =  e 2 x – x.
e 2 x – x.
И, наконец, третий интеграл:
y = ∫ ( e 2 x – x) dx =
e 2 x – x) dx =  e 2 x –
e 2 x –  + C 3.
+ C 3.
Для третьей константы используем последний патрон y (0) =  :
:
y (0) =  – 0 + C 3 =
– 0 + C 3 =  => C 3 = 1.
=> C 3 = 1.
Ответ: частное решение: y =  e 2 x –
e 2 x –  + 1.
+ 1.
В дифференциальном уравнении в явном виде отсутствует функция y
Простейшее уравнение данного типа в общем виде выглядит так: F (x, y', y'') = 0
– всё есть, а «игрека» нет. Точнее, его нет в явном виде, но он обязательно всплывёт в ходе решения.
Кроме того, вместе с «игреком» в явном виде может отсутствовать первая производная:
F (x, y'', y''') = 0 – это уже уравнение третьего порядка.
Может дополнительно отсутствовать и вторая производная:
F (x, y''', yIV) = 0 – уравнение четвертого порядка.
И так далее. Закономерность понятна, и теперь можно без труда определить такое уравнение в практических примерах. Кроме того, во всех этих уравнениях обязательно присутствует независимая переменная «икс».
Как решать такие уравнения? Они решаются с помощью очень простой замены.
Пример 3
Найти общее решение дифференциального уравнения
y'' +  = 9(x + 1).
= 9(x + 1).
Решение: В данном уравнении второго порядка в явном виде не участвует переменная y. Заменим первую производную y' новой функцией p, которая зависит от «икс»: y' = p.
Если y' = p, то y'' = p'.
Цель проведённой замены очевидна – понизить степень уравнения:
p' +  = 9(x + 1).
= 9(x + 1).
Получено линейное неоднородное уравнение первого порядка, с той лишь разницей, что вместо привычной функции «игрек» у нас функция «p». Грубо говоря, отличие только в букве.
Решим вспомогательное уравнение методом «u на v »:
p = uv => p' = u'v + uv' => u'v + uv' +  = 9(x + 1) =>
= 9(x + 1) =>
u'v + u (v' +  ) = 9(x + 1) =>
) = 9(x + 1) =>
1) v' +  = 0 =>
= 0 =>  = –
= – 
 ln v = –ln(x + 1) => v =
ln v = –ln(x + 1) => v =  .
.
2)  = 9(x + 1) => u' = 9(x + 1)2
= 9(x + 1) => u' = 9(x + 1)2  u = 9·
u = 9·  (x + 1)3 + C 1.
(x + 1)3 + C 1.
3) p = y' = uv =  = 3(x + 1)2 +
= 3(x + 1)2 + 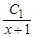 .
.
Для нахождения решения проинтегрируем обе части этого равенства.
Имеем: y =  = (x + 1)3 + C 1 ln| x + 1| + C 2.
= (x + 1)3 + C 1 ln| x + 1| + C 2.
Ответ: Общее решение: y = (x + 1)3 + C 1 ln| x + 1| + C 2.
Пример 4
Найти частное решение уравнения, соответствующее заданным начальным условиям
(1 + sin x) y''' = cos x · y''; y (0) = 1, y' (0) = –1, y'' (0) = 1.
Решение: В данном уравнении третьего порядка в явном виде не участвуют функция y и первая производная y'. Здесь замена: y'' = p.
Если y'' = p, то y''' = p'.
Таким образом, уравнение понижено до первого порядка:
(1 + sin x) p' = cos x · p.
Получено уравнение с разделяющимися переменными, разделяем переменные и интегрируем:
(1 + sin x)  = cos x · p =>
= cos x · p => 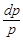 =
= 
 ln | p | = ln |1 + sin x | + ln | C 1| => p = C 1(1 + sin x).
ln | p | = ln |1 + sin x | + ln | C 1| => p = C 1(1 + sin x).
Проведем обратную замену: p = y'': y'' = C 1(1 + sin x).
«Освободимся» от C 1. Из начальных условий y'' (0) = 1 имеем: 1 = C 1(1 + 0) => C 1= 1.
Таким образом, y'' = 1 + sin x.
Найдем искомое частное решение у, проинтегрировав это уравнение два раза, при этом на каждом шаге освобождаясь от С.
Имеем: y' = x – cos x + C 2. Т.к. y' (0) = –1, то –1 = 0 – 1 + C 2 => C 2 = 0. Следовательно, y' = x – cos x.
Интегрируем еще раз и получаем: у =  – sin x + C 3. Т.к. y (0) = 1, то 1 = 0 – 0 + C 3 => => C 3 = 1.
– sin x + C 3. Т.к. y (0) = 1, то 1 = 0 – 0 + C 3 => => C 3 = 1.
Ответ: частное решение: у =  – sin x + 1.
– sin x + 1.
В дифференциальном уравнении
в явном виде отсутствует независимая переменная x
Третий, чуть более сложный тип уравнения, допускающий понижение порядка. Отличительная особенность данного диффура состоит в том, что в нём в явном виде отсутствует независимая переменная «икс». То есть, в исходном дифференциальном уравнении нет «икса».
Пример 5
Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям
(y – 1) y'' = 2(y')2; y (0) = 2, y' (0) = 2.
Решение: В данном уравнении в явном виде не участвует переменная x. Первую производную y' заменим некоторой пока еще неизвестной функцией p (y), которая зависит от функции «игрек »: y' = p (y). Обратите внимание, что функция p (y) – это сложная функция. Внешняя функция – «p», внутренняя функция – «игрек» («игрек» сам по себе является функцией).
Находим вторую производную. По правилу дифференцирования сложной функции:
y'' = (p (y)) ' = p' (y) · y'.
Учитывая, что y' = p (y), окончательно получаем: y'' = (p (y)) ' = p' (y) · y' = p' (y) · p (y).
В принципе, можно запомнить данную замену формально и коротко: y' = p (y), y'' = p' p.
Итак, в исходном уравнении (y – 1) y'' = 2(y')2 проведём нашу замену:
(y – 1) p'p = 2 p 2.
Одно «p» сразу сокращаем: (y – 1) p' = 2 p.
Получено уравнение с разделяющимися переменными. Если p (y) – функция, зависящая от «игрек», то первая производная в дифференциалах расписывается так: p' =  .
.
Не допускать машинальной ошибки – не пишем «привычное» p' =  !!!
!!!
Разделяем переменные и интегрируем:
(y – 1)  = 2 p =>
= 2 p => 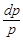 = 2·
= 2· 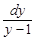
 ln| p | = 2ln| y – 1| + ln| C 1| => p = C 1(y – 1)2.
ln| p | = 2ln| y – 1| + ln| C 1| => p = C 1(y – 1)2.
Проведем обратную замену p (y) = y': y' = C 1(y – 1)2.
Как и в первом параграфе, константу целесообразно «отстрелить» незамедлительно, это значительно упростит дальнейшее интегрирование.
Используем оба начальных условия одновременно: y (0) = 2, y' (0) = 2.
В полученное уравнение y' = C 1(y – 1)2 подставим y = 2 и y' = 2: 2 = C 1(2 – 1)2 => C 1 = 2.
Отсюда: y' = 2(y – 1)2.
Дальнейшее просто:
 = 2(y – 1)2 => ∫
= 2(y – 1)2 => ∫ 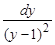 = 2 ∫ dx => –
= 2 ∫ dx => –  = 2 x + C 2.
= 2 x + C 2.
Вторую константу тоже «отстреливаем». Используя начальное условие y (0) = 2, проводим подстановку x = 0, y = 2: –  = 0 + C 2 => C 2 = –1.
= 0 + C 2 => C 2 = –1.
Таким образом: –  = 2 x – 1.
= 2 x – 1.
Выразим частное решение в явном виде:
 = 1 – 2 x => y – 1 =
= 1 – 2 x => y – 1 = 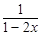 => y = 1+
=> y = 1+ 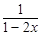 .
.
Ответ: частное решение: y = 1+ 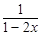 .
.
Пример 6
Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям
y'' + 50 sin y cos3 y = 0; y (0) = 0, y' (0) = 5.
Решение: В данном уравнении в явном виде не участвует переменная x. Еще здесь нет первой производной, но это не должно смущать – важно, что нет «иксов», а значит, используется стандартная замена:
y' = p (y) => y'' = p' p.
Таким образом, степень уравнения понижена до первого порядка:
p' p + 50 sin y cos3 y = 0
Разделяем переменные и интегрируем, не забывая, что p' =  :
:
p  = –50 sin y cos3 y => pdp = –50 sin y cos3 y dy => ∫
= –50 sin y cos3 y => pdp = –50 sin y cos3 y dy => ∫  = 50 ∫ cos3 y d (cos y)=>
= 50 ∫ cos3 y d (cos y)=>
ð 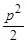 = 50·
= 50·  cos4 y + C ° =>
cos4 y + C ° => 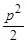 =
=  cos4 y + C ° => p 2 = 25 cos4 y + 2 C °.
cos4 y + C ° => p 2 = 25 cos4 y + 2 C °.
Переобозначим константу 2 C ° через C 1: p 2 = 25 cos4 y + C 1.
Проведём обратную замену p = y': (y')2 = 25 cos4 y + C 1.
Используем одновременно оба начальных условия y (0) = 0, y' (0) = 5 и найдём значение константы C 1. Для этого в полученное уравнение (y')2 = 25 cos4 y + C 1 подставим y = 0 и
y' = 5: 52 = 25· cos40 + C 1 => 25 = 25· 1 + C 1 => C 1 = 0.
Таким образом: (y')2 = 25 cos4 y => y' = 5 cos2 y.
Разделяем переменные и интегрируем:
 = 5 cos2 y => ∫
= 5 cos2 y => ∫  = 5 ∫ dx => tg y = 5 x + C 2.
= 5 ∫ dx => tg y = 5 x + C 2.
В соответствии с начальным условием y (0) = 0:
tg 0 = 5·0 + C 2 => 0 = 0 + C 2 => C 2 = 0.
Окончательно: tg y = 5 x или y = arctg 5 x.
Ответ: частное решение: y = arctg 5 x.
РЕШЕНИЕ ЛИНЕЙНОГО НЕОДНОРОДНОГО УРАВНЕНИЯ 2-ГО ПОРЯДКА