Харьковский национальный университет радиоэлектроники
КОНСПЕКТ ЛЕКЦИЙ (ЧАСТЬ 2)
ПО КУРСУ
«ПРИКЛАДНАЯ ТЕОРИЯ ЦИФРОВЫХ АВТОМАТОВ»
Для студентов дневной формы обучения специальностей
«Специализированные компьютерные системы»
«Компьютерные системы и сети»
«Системное программирование»
УТВЕРЖДЕНО
каф. АПВТ
протокол № від
Харьков 2009
СОДЕРЖАНИЕ
Абстрактный цифровой автомат...................................................................
Определение цифрового автомата......................................................
Типы цифровых автоматов..................................................................
Автомат Мили..............................................................................
Автомат Мура..............................................................................
С-автомат......................................................................................
Способы задания сложных цифровых автоматов..............................
Словесный способ........................................................................
Задание автомата графом переходов..........................................
Табличный способ задания автоматов........................................
Автоматная лента.........................................................................
Задание автомата деревом функционирования..........................
Матричный способ представления..............................................
Связь между автоматами Мили и Мура............................................
Алгоритм трансформации автомата Мура в автомат Мили......
Алгоритм перехода от автомата Мили к автомату Мура..........
4 АБСТРАКТНЫЙ ЦИФРОВОЙ АВТОМАТ
4.1 Определение цифрового автомата
Математической моделью дискретного устройства является абстрактный автомат, определяемый как шестикомпонентный вектор (или кортеж)
S =< A, X, Y, d, l, a 1>.
1. А = { a 1, …, a m, … a M} – множество состояний (алфавит внутренних состояний).
2. Х = { x 1, …, x f, … x F} – множество входных состояний (входной алфавит).
3. Y = { y 1, …, y g, … y G} – множество выходных состояний (выходной алфавит).
4. Функция d: А×Х→А – функция переходов, реализующую сюрьективное отображение d: А×Х на А. Другими словами, функция d некоторым парам «состояние – входной сигнал» (a m, x f) ставит в соответствие состояния автомата a s = d (a m, x f), a sÎ А.
5. Функция l: A×X®Y – функция выходов, реализующая сюрьективное отображение l: A×X на Y. Функция l некоторым парам «состояние - входной сигнал» (a m, x f) ставит в соответствие выходные сигналы автомата y g = l (a m, x f).
6. a 1Î A – начальное состояние автомата.
Определения.
Соответствие G Í A×B это подмножество декартова произведения A×B, где A – множество отправления, а B – множество прибытия.
Соответствие называется всюду определенным, если область определения совпадает со множеством отправления.
Соответствие называется сюрьективным, если область значения совпадает со множеством прибытия.
Образом элемента а в В при соответствии G называется множество всех элементов b Î B, соответствующих элементу a Î А.
Прообразом элемента b в A при соответствии G называется множество всех элементов a Î А, соответствующих элементу b Î B.
Соответствие называется инъективным тогда, когда прообразом любого элемента из области значения является единственный элемент из области определения.
Соответствие называется функциональным тогда, когда образом каждого элемента из области определения является единственный элемент из области значения.
Биективное или взаимнооднозначное соответствие – соответствие, которое является всюду определенным, сюрьективным, инъективным и функциональным.
Функциональное соответствие (функция) из A в B – соответствие, при котором каждому элементу из области определения соответствует единственный элемент из области значения.
Полностью определенная функция из A в B называется отображением A в B.
Если функциональное соответствие (функция) из A в B сюрьективно, то есть любой элемент из B имеет прообраз в A, имеет место сюрьективное отображение, т.е. отображение A на B.
Под алфавитом понимается непустое множество попарно различных символов.
Элементы алфавита называются буквами.
Конечная упорядоченная последовательность букв называется словом в данном алфавите. Из рассмотрения не исключается и пустая последовательность букв (последовательность нулевой длины) – пустое слово, которое будем обозначать буквой e или Х 0.
Абстрактный цифровой автомат (рис.4.1) имеет один вход X и один выход Y. Автомат функционирует в дискретном времени, принимающим целые неотрицательные значения t =0, 1, 2,…. В каждый момент t дискретного времени дискретный автомат (ДА) находится в некотором состоянии a (t) из множества внутренних состояний А, причем, в начальный момент t =0 он всегда находится в начальном состоянии a (0)= a 1. В момент времени t, будучи в состоянии a (t), автомат способен воспринимать на входе букву входного алфавита X (t) Î X. В соответствии с функцией выходов он выдает в тот же момент времени t на выходе букву выходного алфавита y (t)= l [ a (t), x (t)] и в соответствии с функцией переходов d переходит в следующее состояние a (t +1)= d [ a (t), x (t)], a (t) Î A, y (t) Î Y.
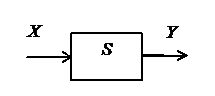
Рисунок 4.1 – Абстрактный автомат
Смысл понятия абстрактного цифрового автомата состоит в том, что он реализует некоторое отображение множества слов входного алфавита Х в множество слов выходного алфавита Y, иначе, если на вход автомата, установленного в начальное состояние a 1 подавать буква за буквой некоторую последовательность букв входного алфавита x (0), x (1), x (2),… – входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита – y (0), y (1), y (2),… – выходное слово.
Таким образом, на абстрактном уровне понятие «работа автомата» понимается как преобразование входных слов в выходные слова. При этом мы отвлекаемся от рассмотрения внутренней структуры абстрактного автомата, рассматривая его как «черный ящик». Так называется принятый в технической кибернетике подход, когда основное внимание уделяется поведению системы относительно внешней среды.
Такое абстрагирование от структуры автомата позволяет решить ряд сложных задач, которые на структурном уровне скрываются за множеством деталей, несущественных с точки зрения функционирования всей системы в целом.
Понятие абстрактного цифрового (дискретного) автомата в теории дискретных устройств воплощает в себе системный подход, при котором предмет или явление рассматривается как нечто целое и основной акцент в исследовании делается на выявлении многообразия связей и отношений с внешней средой, в отличие от структурного подхода, при котором свойства объекта определяются свойствами составляющих его элементов.
Понятие внутреннего состояния в определении автомата вводится в связи с тем, что часто возникает необходимость в описании поведения систем, выходы которых зависят не только от состояний входов в данный момент времени, но и от некоторой предыстории, т.е. от сигналов, которые поступали на входы системы ранее. Состояния как раз и соответствуют некоторой памяти о прошлом, позволяя устранить время как явную переменную и выразить выходной сигнал, как функцию состояния и входа в данный момент времени.
Автоматы с памятью в зависимости от числа внутренних состояний подразделяются на элементарные автоматы (триггеры), число внутренних состояний которых равно двум и сложные цифровые автоматы (ЦА), число внутренних состояний которых более двух.
Известен также класс автоматов, у которых выход не зависит от предыстории и в каждый данный момент определяется лишь входным сигналом в этот же момент времени – это так называемые комбинационные схемы или примитивные автоматы без памяти. Примитивный автомат может быть описан тройкой d = (X, Y, l), где X, Y – входной и выходной алфавиты соответственно, а l: X®Y – функция выходов.
Автомат с памятью генерирует выходные сигналы, зависящие от входного сигнала и внутреннего состояния. На структурном уровне автомат с памятью имеет ряд входных и выходных шин.
Генерация выходных сигналов в комбинационном автомате зависит только от входных сигналов в определенный момент времени и не зависит от того, какие входные сигналы воздействовали на автомат ранее.
4.2 Типы цифровых автоматов
Два типа автоматов получили наибольшее распространение на практике: автомат Мили и Мура, названные так по имени впервые исследовавших эти модели американских ученых G.H. Mealy и E.F. Moore.
4.2.1 Автомат Мили
Функционирование автомата Мили задается уравнениями
a (t +1)= d [ a (t), x (t)];
y (t)= l 1[ a (t), x (t)];
t =0,1,2,…
Рассмотрим в качестве примера упрощенный вариант автомата, продающего в метро жетоны (рис.4.2).
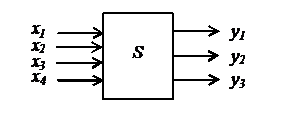
Рисунок 4.2 – Абстрактный автомат Мили по продаже жетонов
Будем считать, что можно класть в автомат только одну купюру за один сеанс выдачи жетонов. И что можно использовать купюры достоинством 2, 5 и 10 гривен. Также есть кнопка «пуск», которая запускает процесс выдачи жетонов, ее должен нажимать покупатель после захвата купюры автоматом.
Т.е. картина работы автомата выглядит следующим образом. Автомат находится в состоянии ожидания, он готов принимать купюры. Покупатель кладет в автомат определенную ограничениями купюру. Нажимает кнопку «пуск» для подтверждения готовности получения жетонов. Затем автомат выдает жетоны и сдачу, после этого автомат переходит в первоначальное состояние ожидания.
В качестве входных воздействий будем использовать:
x 1 – 2 грн., которые покупатель кладет в автомат;
x 2 – 5 грн., которые покупатель кладет в автомат;
x 3 – 10 грн., которые покупатель кладет в автомат;
x 4 – нажатая кнопка «пуск».
В качестве выходных воздействий будем использовать:
y 1 – выдача 1 жетона и 50 копеек;
y 2 – выдача 3 жетонов и 50 копеек;
y 3 – выдача 6 жетонов и 50+50 копеек;
В качестве внутренних состояний автомата будем использовать:
а 1 – состояние ожидания, когда автомат готов принимать купюры;
а 2 – автомат захватил купюру в 2 грн. и ждет нажатия кнопки «пуск»;
а 3 – автомат захватил купюру в 5 грн. и ждет нажатия кнопки «пуск»;
а 4 – автомат захватил купюру в 10 грн. и ждет нажатия кнопки «пуск»;
a 5 – (выдача жетонов) выдача 1 жетона и 50 копеек;
a 6 – (выдача жетонов) выдача 3 жетонов и 50 копеек;
a 7 – (выдача жетонов) выдача 6 жетонов и 50+50 копеек;
На рис. 4.3 представлен граф переходов автомат Мили по продаже жетонов. Вершинам графа соответствуют состояния автомата, а дугам – переходы между состояниями. Входные воздействия определяют условия переходов из состояния в состояние. Входные воздействия указываются над соответствующими дугами перед наклонной. Если входные состояния не указаны, то переход выполняется безусловно. После наклонной указываются выходные сигналы, которые формируются на переходе из состояния в состояние, т.е. выходные сигналы зависят от условия переходов (входных воздействий) и от состояния, в котором находится автомат.
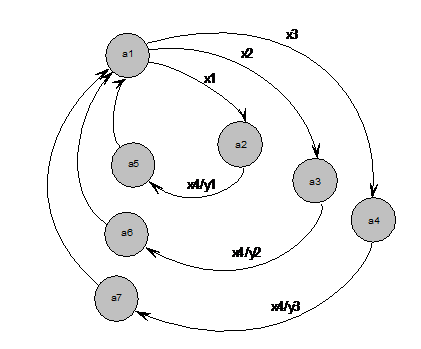
Рисунок 4.3 – Граф переходов абстрактного автомата Мили по продаже жетонов
Автомат переходит из состояния в состояние под действием входных сигналов, т.е. переход в новое состояние зависти от условия перехода. Выходной сигнал будет формироваться во время перехода из состояния в момент времени t в состояние в момент времени t +1. Например, при переходе автомата из состояния a 5 в состояние a 1, будет формироваться выходной сигнал у 1.
4.2.2 Автомат Мура
Функционирование автомата Мура задается уравнениями
a (t +1)= d [ a (t), x (t)];
y (t)= l 2[ a (t)];
t =0,1,2,….
Рассмотрим в качестве примера упрощенный вариант автомата, продающего в метро жетоны, который был рассмотрен раньше. Состояния, входные и выходные сигналы те же. Но выходные сигналы прописаны в вершинах (рис.4.4). Это означает, что выходной сигнал будет формироваться не во время перехода из состояния в момент времени t в состояние в момент времени t +1, а в момент, когда автомат перейдет в состояния в момент времени t. Например, как только автомат перейдет в состояние a 5 будет формироваться выходной сигнал у 1.
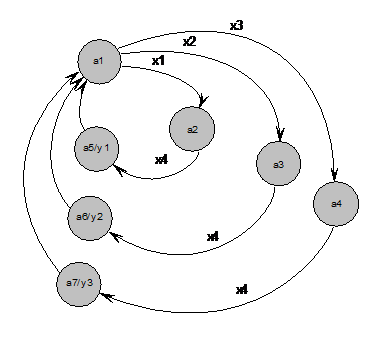
Рисунок 4.4 – Граф переходов абстрактного автомата Мура по продаже жетонов
Автомат Мура отличается от автомата Мили. Его функция выходов зависит только от внутреннего состояния. Поэтому, как только автомат попадает в определенное состояние, тут же формируется выходной сигнал, соответствующий данному состоянию. На графе это отмечается расположением выходных сигналов в вершинах состояний после наклонной или дробной черты.
Выходная функция автомата Мили зависит как от внутреннего состояния, так и от входного сигнала.
4.2.3 С-автомат
Под абстрактным С-автоматом понимается математическая модель цифрового устройства, задаваемого вектором S_C=< A, X, Y, U, d, l 1, l 2, a 1>
В этом векторе:
А – обозначает внутренний алфавит;
Х – обозначает входной алфавит;
Y – обозначает выходной алфавит типа 1 (как у автомата Мили);
U ={ u 1,… u r,… u R} – обозначает выходной алфавит типа 2 (как у автомата Мура);
d: A × X®A, функция переходов, реализующая сюрьективное отображение
d: А × Х на А;
l 1: А × Х→Y – функция выходов, реализующая сюръективное отображение l 1: А × Х на Y;
l 2: А→U – функция выходов, реализующая сюръективное отображение l 2: А→U;
a 1 – обозначает начальное состояние автомата.
С-автомат содержит выходные функции двух типов: типа 1 и типа 2. Т.е. он является сочетанием элементов автоматов и Мили, и Мура.
Функционирование С-автомата задается уравнениями
a (t +1)= d [ a (t), x (t)];
y (t)= l 1[ a (t), x (t)];
u (t)= l 2[ a (t)];
t =0,1,2,…
Рассмотрим в качестве примера упрощенный вариант автомата, продающего в метро жетоны, который был рассмотрен раньше (рис.4.5). Состояния, и входные сигнал остаются те же, но добавляется еще один выходной сигнал:
u 1 – загорается кнопка «пуск».

Рисунок 4.5 – Граф переходов абстрактного С-автомата по продаже жетонов
Здесь за основу взят автомат Мили и добавился выходной сигнал по типу автомата Мура u 1. Как только автомат попадает в состояние а 2 (или а 3, или а 4) должна загораться кнопка «пуск». А когда кнопка «пуск» будет нажата, будет происходить переход в состояние а 1 и выдача жетонов со сдачей.
Автоматы называются дискретными или цифровыми, так как они функционируют во времени дискретно или прерывно (по тактам).
Существуют автоматы синхронные и асинхронные.
Интервалы времени в синхронных автоматах фиксированы и генерируются специальным генератором синхроимпульсов. В асинхронных автоматах моменты дискретного времени определяются изменением состояния памяти или входных сигналов. В компьютерах применяются синхронные цифровые автоматы.
Автомат называется конечным (Finite state machine - FSM), если конечны множества A, X и Y. В дальнейшем будут рассматриваться только конечные автоматы и термин «конечный» может опускаться.
Автомат называется полностью определенным, если область определения функций переходов d и функций выхода l = D d= D l= А × Х. Другими словами, область определения d и l совпадают с множеством А × Х – множеством всевозможных пар (a m, x f). У не полностью определенного, или частичного, автомата функции d и l определены не для всех пар (a m, x f) Î А × Х.
В данной дисциплине будут изучаться только детерминированные автоматы, у которых выполнено условие однозначности переходов: автомат, находящийся в некотором состоянии, под действием любого входного сигнала не может перейти в более чем в одно состояние.
4.3 Способы задания сложных цифровых автоматов
Существует несколько способов задания цифровых автоматов
4.3.1 Словесный способ
Он представляет собой словесное описание поведения автомата (было рассмотрено в предыдущем пункте).
4.3.2 Задание автомата графом переходов
Представление автоматов графом переходов называется также графическим представлением. При этом способе автомат задается графом переходов (ГП). Граф переходов – ориентированный граф, вершины которого соответствуют состояниям автомата, а дуги – переходам. Две вершины a m и a s соединяются дугой, если в автомате имеется переход из a m в a s. Дуга отмечается входным сигналом x f и выходным сигналом y g.
Если выходной сигнал не определен, ставится прочерк (тире). Максимальное количество дуг, выходящих из вершины графа, равно числу букв входного алфавита.
Если переход из состояния a m в состояние a s вызывается многими входными сигналами, то дуги отмечаются всеми этими сигналами.
Автомат Мура задается графом переходов, в котором выходной сигнал записывается внутри вершины или рядом с ней.
На рис.4.3, 4.4 и 4.5 изображены графы переходов автомата Мили, Мура и С-автомата соответственно.
4.3.3 Табличный способ задания автоматов
Автомат Мили задается таблицей переходов – ТП (табл. 4.1) и таблицей выходов – ТВ (табл. 4.2) В случае не полностью определенного автомата, таблица переходов или таблица выходов не полностью заполнены и в них имеются пустые позиции. Таблицы построены на основании графа переходов автомата рис. 4.3.
Таблица 4.1 – Таблица переходов автомата Мили
| ТП | а 1 | а 2 | а 3 | а 4 | а 5 | а 6 | а 7 |
| х 1 | а 2 | - | - | - | - | - | - |
| х 2 | а 3 | - | - | - | - | - | - |
| х 3 | а 4 | - | - | - | - | - | - |
| х 4 | - | а 5 | а 6 | а 7 | - | - | - |
| - | - | - | - | а 1 | а 1 | а 1 |
Таблица 4.2 – Таблица выходов автомата Мили
| ТВ | а 1 | а 2 | а 3 | а 4 | а 5 | а 6 | а 7 |
| х 1 | - | - | - | - | - | - | - |
| х 2 | - | - | - | - | - | - | - |
| х 3 | - | - | - | - | - | - | - |
| х 4 | - | y 1 | y 2 | y 3 | - | - | - |
| - | - | - | - | - | - | - |
На пересечении столбца a i и строки x j в таблице переходов записывается состояние перехода a s(t +1)= d [ a m(t), x f(t)], в которое автомат переходит из состояния a m под действием сигнала x f, а в таблице выходов – соответствующий этому переходу выходной сигнал y (t)= l [ a m(t), x f(t)].
Как нам известно, выходной сигнал автомата Мура зависит только от внутреннего состояния. Поэтому автомат Мура может быть задан одной отмеченной таблицей переходов (табл. 4.3). Таблица построена на основании графа переходов автомата рис. 4.4.
Таблица 4.3 – Отмеченная таблица переходов автомата Мура
| ОТП | - | - | - | - | y 1 | y 2 | y 3 |
| а 1 | а 2 | а 3 | а 4 | а 5 | а 6 | а 7 | |
| х 1 | а 2 | - | - | - | - | - | - |
| х 2 | а 3 | - | - | - | - | - | - |
| х 3 | а 4 | - | - | - | - | - | - |
| х 4 | - | а 5 | а 6 | а 7 | - | - | - |
| - | - | - | - | а 1 | а 1 | а 1 |
С-автомат задается двумя таблицами таблицей переходов и отмеченной таблицей выходов или наоборот отмеченной таблицей переходов и таблицей выходов (табл. 4.4 и табл. 4.5). Таблицы построены на основании графа переходов автомата рис. 4.5.
Таблица 4.4 – Отмеченная таблица переходов С-автомата
| ОТП | - | u 1 | u 1 | u 1 | - | - | - |
| а 1 | а 2 | а 3 | а 4 | а 5 | а 6 | а 7 | |
| х 1 | а 2 | - | - | - | - | - | - |
| х 2 | а 3 | - | - | - | - | - | - |
| х 3 | а 4 | - | - | - | - | - | - |
| х 4 | - | а 5 | а 6 | а 7 | - | - | - |
| - | - | - | - | а 1 | а 1 | а 1 |
Таблица 4.5 – Таблица выходов С-автомата
| ТВ | а 1 | а 2 | а 3 | а 4 | а 5 | а 6 | а 7 |
| х 1 | - | - | - | - | - | - | - |
| х 2 | - | - | - | - | - | - | - |
| х 3 | - | - | - | - | - | - | - |
| х 4 | - | y 1 | y 2 | y 3 | - | - | - |
| - | - | - | - | - | - | - |
4.3.4 Автоматная лента
Автомат может быть задан с помощью автоматной ленты или ленты Тьюринга (табл. 4.6).
Таблица 4.6 – Автоматная лента Тьюринга
| Такт | ||||||||||
| Входной сигнал | х 1 | х 4 | - | х 2 | х 4 | - | х 3 | х 4 | - | |
| Состояние | а 1 | а 2 | а 5 | а 1 | а 3 | а 6 | а 1 | а 4 | а 7 | а 1 |
| Выходной сигнал | - | y 1 | - | - | y 2 | - | - | y 3 | - |
Таблица 4.6 построена по табл. 4.1 и табл. 4.2 автомата Мили и содержит 4 строки – номер такта, входной сигнал, состояние и выходной сигнал. Особенность такой ленты состоит в том, что для любой пары соседних тактов t и t +1 можно выделить четверку символов (выделена жирной линей в табл. 4.6), которая показывает в какое состояние перейдет цифровой автомат в такте t +1 и какой выходной сигнал будет сформирован под действием входного сигнала.
Тьюринг (английский ученый, занимавшийся исследованиями конечных автоматов) показал, что любому конечному автомату соответствует эквивалентная ему машина Тьюринга, функционирование которой можно задавать лентой Тьюринга.
4.3.5 Задание автомата деревом функционирования
Автомат может быть задан модификацией графа переходов, называемого деревом функционирования. Этот способ задания имеет то преимущество, что позволяет проанализировать работу автомата такт за тактом.
Вершины дерева отмечены состоянием автомата (рис. 4.6)
Автомат начинает функционировать из состояния a 1 и далее переходит к другим возможным состояниям под действием входного сигнала x j. Дерево на рис. 4.6 построено по автоматной ленте (табл. 4.6)
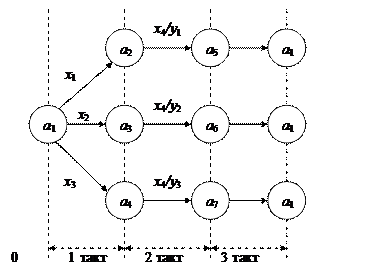
Рисунок 4.6 – Дерево функционирования абстрактного автомата Мили по продаже жетонов
4.3.6 Матричный способ представления
Любой автомат может быть задан матрицей соединений. Матрица соединений С имеет M строк и M столбцов. Каждая строка соответствует исходному состоянию a m(t), каждый столбец состоянию перехода a s(t +1). На пересечении строки i и столбца j записывается элемент C ij. Этот элемент включает числитель и знаменатель.
Числитель отображает условие перехода (входной сигнал x f) автомата из состояния a m в состояние a s. Знаменатель отображает выходной сигнал y g(t), генерируемый на переходе.
Составим матрицу соединений С для автомата Мили заданного таблицей переходов (табл. 4.1) и таблицей выходов (табл. 4.2).
| а 1 | а 2 | а 3 | а 4 | а 5 | а 6 | а 7 | ||
| а 1 | - | х 1 /- | х 2 /- | х 3 /- | - | - | - | |
| а 2 | - | - | - | - | х 4 /y 1 | - | - | |
| а 3 | - | - | - | - | - | х 4 /y 2 | - | |
| С = | а 4 | - | - | - | - | - | - | х 4 /y 3 |
| а 5 | 1/- | - | - | - | - | - | - | |
| а 6 | 1/- | - | - | - | - | - | - | |
| а 7 | 1/- | - | - | - | - | - | - |
Этот способ не удобен при возрастании числа внутренних состояний, число нулевых элементов матрицы возрастает (причиной этого является слабая взаимосвязанность внутренних состояний графов переходов цифровых автоматов), что ведет к увеличению расхода памяти в компьютерах.
4.4 Связь между автоматами Мили и Мура
4.4.1 Алгоритм трансформации автомата Мура в автомат Мили
Два автомата SA и SB с одинаковыми входными и выходными алфавитами называются эквивалентными, если после установления их в начальные состояния их реакция (выходное слово) на любое входное слово совпадает.
Если для автомата Мили (табл. 4.7 и табл. 4.8) и автомата Мура (табл. 4.9) найти их реакции на входное слово x1 x2 x1 x2 x2, то получим следующие две ленты (табл. 4.10 и табл. 4.11).
Таблица 4.7 – Таблица переходов автомата Мили
| ТП | а 1 | а 2 | а 3 |
| х 1 | a 2 | a 3 | a 2 |
| х 2 | a 3 | a 2 | a 1 |
Таблица 4.8 – Таблица выходов автомата Мили
| ТВ | a 1 | а 2 | а 3 |
| х 1 | u 1 | u 3 | u 3 |
| х 2 | u 2 | u 1 | u 1 |
Таблица 4.9 – Отмеченная таблица переходов автомата Мура
| ОТП | u 1 | u 1 | u 3 | u 2 | u 3 |
| a 1 | a 2 | a 3 | a 4 | a 5 | |
| х 1 | a 2 | a 5 | a 5 | a 3 | a 3 |
| х 2 | a 4 | a 2 | a 2 | a 1 | a 1 |
Таблица 4.10 – Лента Тьюринга для автомата Мили
| Такт | |||||||
| Х | x 1 | x 2 | x 1 | x 2 | x 2 | ||
| A | a 2 | a 2 | a 2 | a 3 | a 1 | a 3 | |
| Y | u 1 | u 1 | u 3 | u 1 | u 2 | ||
Таблица 4.11 – Лента Тьюринга для автомата Мура
| Такт | |||||||
| Х | x 1 | x 2 | x 1 | x 2 | x 2 | ||
| A | a 2 | a 2 | a 2 | a 5 | a 1 | a 4 | |
| Y | u 1 | u 1 | u 1 | u 3 | u 1 | u 2 | |
Из сравнения лент двух автоматов Мили и Мура видно, что их реакции (реакции автомата Мили и сдвинутой на один такт реакции автомата Мура) совпадают.
Выходным сигналом автомата Мура в такт t =0 пренебрегаем, так как он определяется не входным сигналом автомата в этот момент времени, а исключительно состоянием.
Из сравнения двух лент, конечно, не следует делать вывод, что оба автомата SA и SB эквивалентны, так как исследование проведено только для одного входного слова, а не для всех допустимых (разрешенных) входных слов. Известно изначально, что они эквивалентны.
При рассмотрении алгоритмов взаимной трансформации одного типа в другой будем (в соответствии с изложенным выше) пренебрегать в автоматах Мура выходным сигналом l (a 1), связанным с начальным состоянием.
Рассмотрим вначале преобразование автомата Мура в автомат Мили. Пусть дан автомат Мура
SA ={ AA, XA, YA, dA, lA, a 1 A }, у которого
AA ={ a1,…,am };
XA = { x1,…,xF };
YA ={ u1,…,uG };
dA: AA × XA ® AA;
lA: AA®YA,
a 1 A = a 1 – начальное состояние.
Построим автомат Мили SB ={ AB, XB, YB, dB, lB, a 1 B }, у которого AB=AA; XB=XA; YB=YA; dB=dA; a 1 B =a 1 A =a 1. Функцию выходов lB: AB × XB ® YB определим следующим образом: если в автомате Мура dA (am, xf)=as и lA(as)=ug, то в автомате Мили lB(am,xf)=ug.
Переход от автомата Мили при графическом способе задания автомата иллюстрируется фрагментом графа переходов на рис. 4.7.
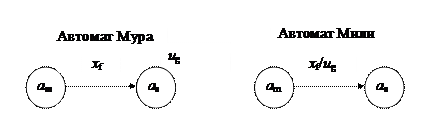
Рисунок 4.7 – Переход от автомата Мура к автомату Мили
При переходе от автомата Мура к автомату Мили выходной сигнал ug, записанный рядом с вершиной as, переносится на все дуги, входящие в эту вершину.
При табличном способе задания автомата Мура (отмеченной таблицей переходов) таблица переходов автомата Мили совпадает с таблицей переходов автомата Мура. В таблице выходов снимается только отметка состояний автомата Мили путем замены символа состояния перехода as символом выходного сигнала ug, отмечающего столбец as в таблице переходов автомата Мура.
Из самого способа построения автомата Мили SB следует, что он эквивалентен автомату Мура SA. В качестве примера перехода от автомата Мура к автомату Мили, представленных графом переходов можно привести примеры на рис. 4.3 (Мили) и 4.4 (Мура).
Рассмотрим пример перехода от ОТП автомата Мура (табл. 4.9) к автомату Мили, представленному таблицей переходов и таблицей выходов. В результате получим табл. 4.12 и табл. 4.13.
Таблица 4.12 – Таблица переходов автомата Мили
| ТП | а 1 | а 2 | а 3 | a 4 | a 5 |
| х 1 | a 2 | a 5 | a 5 | a 3 | a 3 |
| х 2 | a 4 | a 2 | a 2 | a 1 | a 1 |
Таблица 4.13 – Таблица выходов автомата Мили
| ТВ | a 1 | а 2 | а 3 | a 4 | a 5 |
| х 1 | u 1 | u 3 | u 3 | u 3 | u 3 |
| х 2 | u 2 | u 1 | u 1 | u 1 | u 1 |
4.4.2 Алгоритм перехода от автомата Мили к автомату Мура
Прежде чем рассмотреть трансформацию автомата Мили в автомат Мура, наложим на автомат Мили следующее ограничение, в нем не должно быть преходящих состояний. Под преходящим будем понимать состояние, в котором при представлении автомата графом переходов не входит ни одна дуга, но которое имеет по крайней мере одну выходящую дугу.
Итак, пусть задан автомат Мили SA ={ AA, XA, YA, dA, lм, a 1 A }, где
AA ={ a 1 ,…,am };
XA = { x 1 ,…,xF };
YA ={ u 1 ,…,uG };
dA: AA × XA ® AA;
lA: AA × XA ® YA,
a 1 A = a 1 – начальное состояние.
Построим автомат Мура SB ={ AB, XB, YB, dB, l
Поделиться:
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2018-01-08
Нарушение авторских прав и Нарушение персональных данных