Принципы построения активных RC-фильтров

Рассмотрим основы построения активных RC-фильтров с обратными связями [6]. Активные RC-фильтры НЧ первого порядка получаются, если во входной цепи ОУ включить активное сопротивление, а в цепи отрицательной обратной связи – частотно-зависимую RC-цепь в виде параллельного соединения сопротивления и емкости (рисунок 8.9).

Рисунок 8.9 – Активный RC-фильтр нижних частот 1-го порядка

Комплексная передаточная функция такого фильтра описывается выражением:

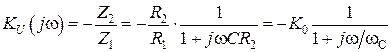, (8.8)

где - коэффициент усиления по постоянному току, а - частота среза фильтра.

Если в цепь обратной связи ОУ включить активное сопротивление, а во входной цепи поместить частотно-зависимую RC-цепь в виде последовательного соединения сопротивления и емкости, то получится активный RC-фильтр верхних частот первого порядка (рисунок 8.10).

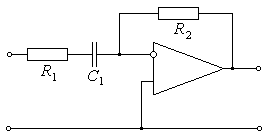
Рисунок 8.10 – Активный RC-фильтр верхних частот 1-го порядка

Комплексная передаточная функция такого фильтра описывается выражением:

, (8.9)

где - коэффициент усиления по постоянному току, а - частота среза фильтра.

Другим способом реализации активных RC-фильтров [6] является использование ОУ в качестве преобразователя сопротивления (рисунок 8.11).

Подключение такой ячейки на выходе Г-образного RC-фильтра нижних или верхних частот обеспечивает, с одной стороны, возможность работы фильтра при любой нагрузке, а, с другой стороны, позволяет регулировать величину коэффициента усиления всей схемы, так как коэффициент усиления данной ячейки не зависит от частоты и составляет:

. (6.10)

Рисунок 8.11 – Использование ОУ в качестве преобразователя сопротивлений при построении активных RC-фильтров

Построение фильтров нижних и верхних частот второго порядка осуществляется по одной из трех схем [6]: использование сложной отрицательной обратной связи (ООС), использование положительной обратной связи (ПОС), использование омической отрицательной обратной связи. Примеры таких активных RC-фильтров нижних частот представлены на рисунках 8.12 – 8.14. Соответствующие фильтры верхних частот получаются простой заменой в схеме фильтра нижних частот всех сопротивлений (за исключением сопротивлений в ветви обратной связи преобразователя сопротивлений) на емкости, а всех емкостей – на сопротивления.

Рисунок 8.12 – Активный RC-фильтр нижних частот второго порядка на основе сложной ООС

Комплексная передаточная функция фильтра на основе сложной ООС имеет вид:

(8.11)

Задание коэффициентов , и в соответствии с выбранной аппроксимацией АЧХ (Баттерворта, Чебышева, Бесселя и пр.) позволяет определять любые три из пяти номиналов через два других. Обычно используемые в фильтрах емкости обладают большим разбросом параметров, нежели сопротивления. Поэтому, как правило, при разработке принципиальной схемы фильтра задаются именно значениями емкостей, а значения сопротивлений рассчитывают.

Рисунок 8.13 – Активный RC-фильтр нижних частот второго порядка на основе сложной ПОС

Использовании в схеме активного RC-фильтра ОУ с ПОС предполагает постоянство его коэффициента усиления. Этого добиваются соответствующим выбором сопротивлений ветви ООС. При указанном на рисунке 8.13 выборе этих сопротивлений коэффициент усиления ОУ, согласно выражению (8.10) составляет . ПОС в такой схеме обусловлена наличием емкости . Схема значительно упрощается, если использовать некоторые предварительные ограничения. Так, если положить, что 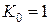, то сопротивления и из схемы могут быть исключены. Получающийся в результате ОУ с ООС представляет собой повторитель напряжения и выпускается промышленностью в виде отдельной микросхемы.

Комплексная передаточная функция такого активного RC-фильтра имеет вид:

(8.12)

Как и в случае использования сложной ООС значения коэффициентов и 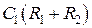задаются в соответствии с выбранной аппроксимацией АЧХ фильтра. Тогда, задавая значения емкостей, можно определить значения сопротивлений. Несколько упростить анализ можно положив сопротивления и емкости попарно одинаковыми. Тогда комплексная передаточная функция фильтра, при условии, что примет вид:

(8.13)

Недостатком данной схемы является трудность задания значений , близких к трем, так как при таком выборе схема возбуждается и становится генератором гармонических колебаний. Однако данная схема обладает и рядом достоинств. Так задавая различные значения при одних и тех же значениях и 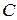, можно легко получать фильтры различного типа. Кроме того, использование для одновременного изменения сопротивлений и 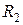сдвоенного сопротивления позволяет легко изменять величину частоты среза фильтра.

Использование в схемах активных RC-фильтров омической ООС предполагает использование ОУ с внутренней коррекцией частотной характеристики (на схеме рисунка 8.14 обозначена корректирующей емкостью 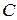). Однако при этом граничная частота работы ОУ должна быть как можно большей.

Рисунок 8.14 – Активный RC-фильтр нижних частот второго порядка на основе омической ООС

Полосовые фильтры обычно реализуются либо за счет использования сложной ООС (рисунок 8.15), либо за счет использования ПОС (рисунок 8.16).

Комплексная передаточная функция полосового фильтра на основе сложной ООС при условии равенства емкостей определяется выражением:

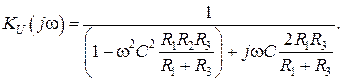(8.14)

Рисунок 8.15 - Активный полосовой RC-фильтр второго порядка на основе сложной ООС

Резонансная частота такого фильтра определяется номиналами всех сопротивлений и емкостей и задается выражением:

. (8.15)

Добротность такого полосового фильтра определяется лишь соотношением между сопротивлениями и составляет:

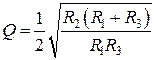. (8.16)

Данная схема обладает тем преимуществом, что она не склонна к генерации на резонансной частоте при недостаточно точном подборе номиналов элементов. Однако непременным условием при этом является наличие частотной коррекции ОУ.

Рисунок 8.16 - Активный полосовой RC-фильтр второго порядка на основе ПОС

Схема полосового фильтра на основе ОУ с ПОС, как и в случае фильтров НЧ и ВЧ содержит в своем составе ветвь с ООС, позволяющей задавать постоянный коэффициент усиления ОУ равный . Недостатком схемы является зависимость между резонансным коэффициентом усиления и добротностью фильтра. Однако схема обладает и рядом достоинств: добротность можно менять, изменяя коэффициент усиления ОУ в пределах от нуля до трех. При этом резонансная частота фильтра остается неизменной. При достижении значения 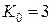схема самовозбуждается.

Как и в случае с активными фильтрами НЧ и ВЧ второго порядка можно использовать внутреннюю частотную коррекцию ОУ и омическую ООС для создания полосового фильтра второго порядка на высоких частотах. Для этого можно использовать схему рисунка 8.14, но снимать напряжение не с выхода второго каскада, а с выхода первого каскада.

Режекторный RC-фильтр второго порядка может быть построен с использование двойного Т-образного моста (рисунок 8.17) или с использованием моста Вина-Робинсона (рисунок 8.18).

Рисунок 8.17 - Активный режекторный RC-фильтр второго порядка на основе двойного Т-образного моста

Рисунок 8.18 - Активный режекторный RC-фильтр второго порядка на основе моста Вина-Робинсона

В случае двойного Т-образного моста добротность пассивного RC-фильтра составляет 0,25. Чтобы ее повысить данный мост включают в цепь ПОС операционного усилителя. Резонансная частота такого фильтра определяется выражением:

. (8.17)

Для правильной работы такого активного фильтра необходим оптимальный выбор резонансной частоты и коэффициента усиления, что является затруднительным особенно при больших значениях добротности. Такого недостатка лишен режекторный фильтр на основе моста Вина-Робинсона и поэтому он является более предпочтительным.

Несмотря на то, что при отсутствии ОУ добротности двойного Т-образного моста и моста Вина-Робинсона не слишком отличаются, включение последнего в цепь обратной связи усилителя позволяет получать любое значение добротности. Резонансная частота такого фильтра перестраивается путем изменения обоих сопротивлений 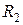и емкостей 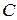, а также путем плавной подстройки путем незначительного изменения сопротивления .