Вы все, наверное, в курсе последовательности Фибоначчи и связанным с ней числом Фидия (золотым сечением), хочу напомнить, «расширшить и углубжить» эти понятия.
Для начала, повторим известный материал:
1. Последовательность Фибоначчи:
Рекуррентная формула: 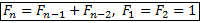
Итого, имеем посл-ть: 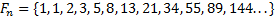
Отмечу запоминающиеся числа: 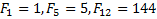
2. Классическое определение золотого сечения: отношение целого к большей части = отношению большей части к меньшей, т.е., считая целое за 1, а большую часть за 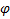 , имеем:
, имеем: 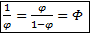 ,
,
т.е. 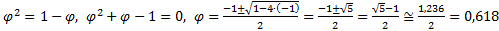
или 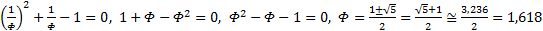
они отличаются на 1, и верно: 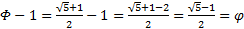
или же 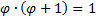 , это перезапись первого уравнения, подставив в него
, это перезапись первого уравнения, подставив в него 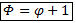 , получим
, получим
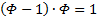 , а это перезапись второго.
, а это перезапись второго.
Для удобства сегодняшней темы, будем использовать второе уравнение с заглавной 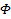
Имеем:
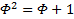 , помножим обе части на
, помножим обе части на 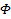 , получим:
, получим:
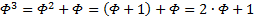 , ещё несколько раз:
, ещё несколько раз:
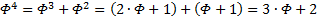
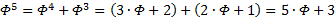
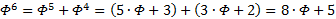
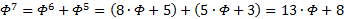
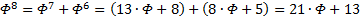
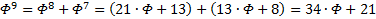
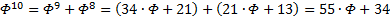
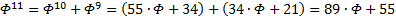
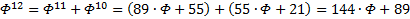
Иными словами, помножив оригинал на 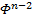 , будем иметь
, будем иметь
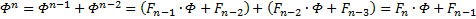
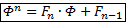
Отмечу схожесть формул посл-ти Фибоначчи и степеней золотого сечения: если организовать последовательность 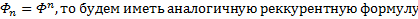
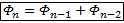
Похоже, предел отношения 2-х соседних членов в посл-х с одинаковой рекуррентной формулой одинаков…
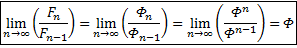
Если повторить все те же шаги для 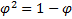 , то придём к следующей формуле:
, то придём к следующей формуле:
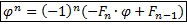
рекуррентная формула:
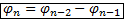
1-е Отступление от сегодняшней темы: введение в мою «золотую» арифметику:
Глянув на определение гипероператора, я понял, что он не эстетичен
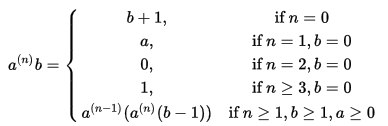
В 2-х словах: он описывает повтор бинарных операций, порождая новое действие, как то умножение – повтор сложения, возведение в степень – повтор умножения и пр.
Роль нуля как второго аргумента выглядит абсолютно дисгармонично и НЕ ЕДИНООБРАЗНО, посему я придумал свой гипероператор: в нём второй аргумент, равный 0, не меняет первого, потому как означает количество повторов операций предыдущего уровня, а не операндов, т.е., я изменил «дважды два – четыре» J
Сложение я решил оставить прежним, хотя был вариант и с его изменением (когда на роль «неменятеля» я назначил 1)… Итак:
2⊡2=2+2+2=6 (2 плюса)
2⊡5=2+2+2+2+2+2=12 (5 плюсов, соответственно - 6 слагаемых)
Короче, 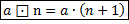
С возведением в степень есть нюанс:
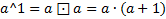
Но что есть, примеру, 5^2? Есть 2 варианта:
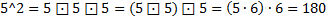 или
или
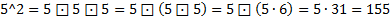 Прижатие скобок влево назовём левой операцией возведения в степень, второй пример, соответственно – правое возведение в степень. Т.к. моё умножение не коммутативно, начиная с возведения в степень
Прижатие скобок влево назовём левой операцией возведения в степень, второй пример, соответственно – правое возведение в степень. Т.к. моё умножение не коммутативно, начиная с возведения в степень
(это 3-й уровень: 2-й – умножение, 1-й сложение), гипероператор будет делиться на левый и правый:
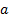 Л
Л 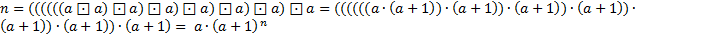
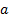 П
П 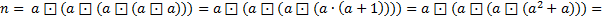
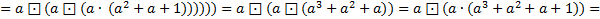
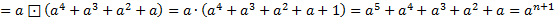 +
+ 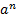 …+
…+ 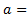
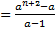 ,
,
1П 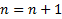
Проверим приведённый выше пример:
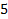 Л
Л 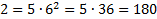
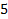 П
П 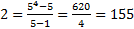
Ещё немножко общих примеров:
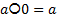 , где
, где 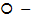 любой гиператор уровня
любой гиператор уровня 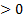
1П 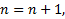 где П
где П 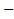 любой правый гиператор уровня
любой правый гиператор уровня 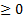
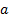 Л
Л 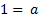 П
П 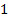 , на уровнях от 1 до 3
, на уровнях от 1 до 3
Нулевой уровень – это база - инкрементация, которая ничего не повторяет, и определение 0, как второго аргумента, не меняющего первый, здесь не работает, однако дам и для него определения, здесь тоже есть деление на левый и правый, оно нужно для единого определения левых и правых гиперов
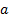 Л0
Л0 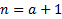
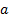 П0
П0 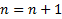
Теперь общее рекуррентное определение левого и правого гипера уровня p 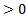 для целого положительного второго аргумента
для целого положительного второго аргумента
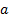 Лp Лp 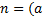 Лp Лp 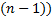 Лp-1 Лp-1 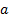
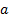 Пp Пp 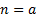 Пp-1 Пp-1 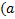 Пp Пp 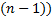
|
Из определения базового нулевого уровня и общей формулы, в частности, следует, что + одинаков, что левый, что правый (в левом случае мы будем инкрементировать первый аргумент то кол-во раз, которое указано во втором, в правом – всё наборот, а результат - один). Покамест хватит о «золотой арифметике», а теперь для чего я изложил её некоторые определения:
Если рассмотреть 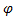 Л1
Л1 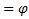 П1
П1 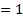 , получим знакомую формулу
, получим знакомую формулу 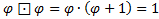 , забегая несколько вперёд, дам золотые сечения вычисленных уровней
, забегая несколько вперёд, дам золотые сечения вычисленных уровней
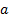 Л1
Л1 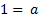 П11
П11 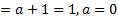
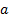 Л2
Л2 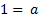 П21
П21 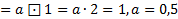
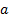 Л3
Л3 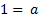 П31
П31 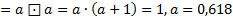
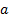 Л4
Л4 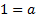 Л
Л 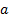 =
= 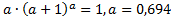
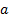 П41
П41 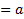 П
П 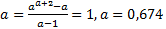
То золотое сечение, что было рассмотрено, - 3 уровня. Если рассматривать левый вариант этого уровня, то можно выйти на обобщённые золотые сечения, которые, в частности активно пытается продвигать мой тёзка Стахов, тоже Алексей Петрович, разница между нашими результатами заключается в том же, что и разница между большой и малой Фи, т.е. в 1-це, я предпочитаю за целое брать 1, и ОЗС у меня получаются ≤ 1, но суть-то не меняется… Итак рассмотрим моё определение ОЗС, его порядок будет указан в нижнем индексе.
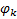 Л
Л 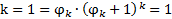 или
или 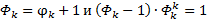
Уже рассмотренное ОЗС было 1 порядка, и ему соответствовали стандартные числа Фибоначчи, т.е. того же порядка, расширим определение последовательности через рекуррентную формулу:
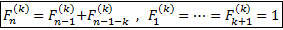
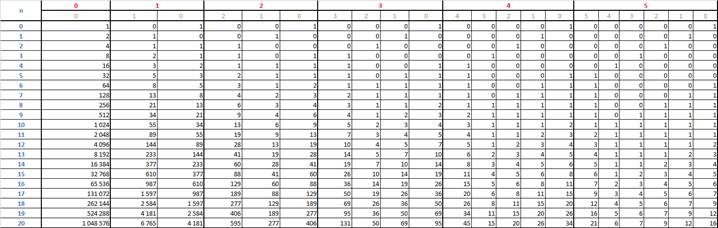
Теперь весёлая табличка с ними
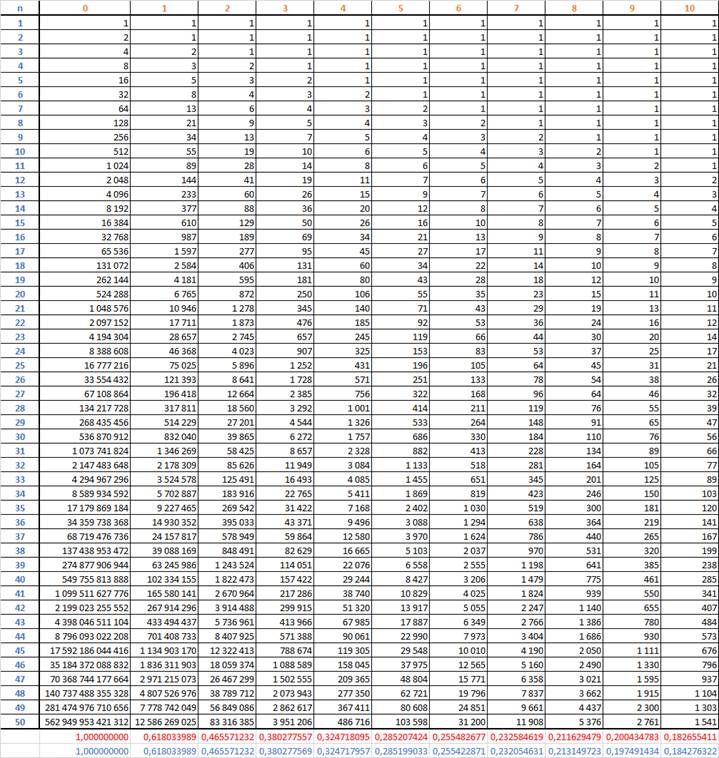
Верхняя строка – номер порядка посл-ти (0-ю и 1-ю, надеюсь, узнали), снизу 2 строки касаются ОЗС k-го порядка (красная – отношение 2-х последних посчитанных членов - 1, а синяя – то, что должно быть в пределе такого деления, т.е. ОЗС k-го порядка, вычисленные, исходя из приведённых мною уравнений «золотой арифметики», т.е. 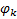
Теперь повторим процедуру получения формулы для выражения степеней ОЗС, используя числа Фибоначчи, соответствующего порядка. Рассмотрим ОЗС 2 порядка, как и в первый раз, будем играться с заглавными Фи (с мелкими выше первого уровня так не получается…
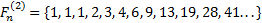
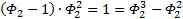
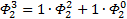
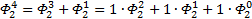
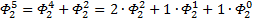
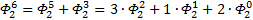
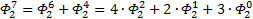
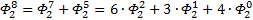
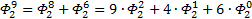
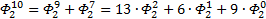
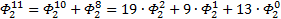
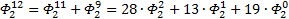
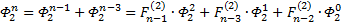
Я чуть сменил шаблон формул, прописав единичные коэффициенты и степени, а также добавив элемент в 0-вой степени, сейчас поймёте, зачем. Картинка с общей формулой уже почти полностью нарисовалась, но есть предложение закрепить материал на 3-ке и глянуть на вырожденный 0-й вариант со степенями 2-к
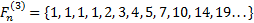
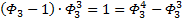
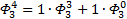
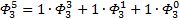
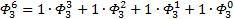
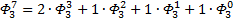
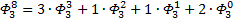
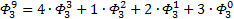
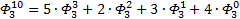
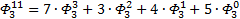
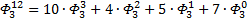
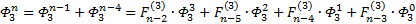
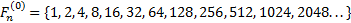
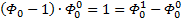
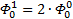
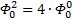
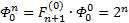
Надеюсь, что теперь данная таблица коэффициентов степеней разложения 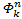 по базовым степеням будет всем понятна и без подробного описания
по базовым степеням будет всем понятна и без подробного описания
Что ж, нарисуем общую формулу, просится, зараза…
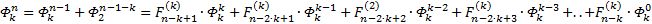
Обращаю ваше внимание, что
1. одиночные 1 соответствуют таким же степеням ОЗС, ибо они не раскрываются, они базис, их 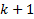
2. все эти члены будут с коэффициентами 1 при 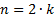
3. у всех коэффициентов, имеются нулевые дырки размером 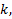 при члене со старшей степени, она начинается с 0-й степени ОЗС, после нулевой дырки у всех затем идёт период
при члене со старшей степени, она начинается с 0-й степени ОЗС, после нулевой дырки у всех затем идёт период 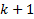 единиц, ну, и ещё далее продолжают браться следующие члены посл-ти данного порядка
единиц, ну, и ещё далее продолжают браться следующие члены посл-ти данного порядка