Расчетное задание №1. Законы Ньютона. Законы сохранения.
ВМ1
ЗАКОНЫНЬЮТОНА
К концам невесомой и нерастяжимой нити, перекинутой через невесомый блок, подвешены грузы: слева n одинаковых тел массой m каждый, соединённых невесомыми нерастяжимыми нитями; справа – груз массой М. Найти:
Œ силу натяжения нити между i и i + 1 телами; построить график Т=f(i);
модуль результирующей силы, действующей на i тело; построить график
а = f(i);
Ž модуль результирующей силы, действующей на группу из k тел, расположенных ниже i тела; построить график | R |= f(k);
модуль разности сил натяжения нитей, прикреплённых к группе из k тел, расположенных ниже i тела; построить график | R |= f(k).
Числовые данные
| № | А | М, кг | m, г | n | i | k | № | А | М, кг | m, г | n | i | k |
| 1,0 | 1,5 | ||||||||||||
| 1,0 | 1,5 | ||||||||||||
| 1,0 | 2,0 | ||||||||||||
| 1,0 | 2,0 | ||||||||||||
| 2,0 | |||||||||||||
| 2,0 | |||||||||||||
| 2,5 | |||||||||||||
| 2,5 | |||||||||||||
| 2,5 | |||||||||||||
| 2,5 | |||||||||||||
| 3,0 | |||||||||||||
| 3,0 | |||||||||||||
| 1,5 | 3,0 | ||||||||||||
| 1,5 | 3,0 |
№ – номер варианта (порядковый номер фамилии студента в группе),
А – номер вопроса для данного варианта.
ЗАКОНЫСОХРАНЕНИЯ
Пуля массой m, летевшая горизонтально со скоростью v попадает в неподвижно лежащий на горизонтальной поверхности (коэффициент трения между поверхностью и бруском m) брусок массы М. После взаимодействия пули с бруском скорость пули в горизонтальном направлении стала равной k v.
1. Сколько времени t будет двигаться брусок после соударения с пулей?
2. Какое расстояние s будет пройдено бруском после соударения с пулей?
3. Найти относительное изменение кинетической энергии системы пуля-брусок за время соударения.
4. Какую долю e составляет кинетическая энергия бруска от полной кинетической энергии пули и бруска до взаимодействия?
Числовые данные
| № | А | m, г | u, м/с | M, кг | m, 10-2 | k | № | А | m, г | u, м/с | M, кг | m, 10-2 | k |
| 4,0 | 2,50 | -0,20 | 6,0 | 4,50 | 0,50 | ||||||||
| 4,0 | 2,50 | -0,20 | 6,0 | 4,50 | 0,50 | ||||||||
| 4,0 | 2,50 | -0,20 | 0,10 | 0,5 | 0,60 | ||||||||
| 4,0 | 2,50 | -0,20 | 0,10 | 0,5 | 0,60 | ||||||||
| 5,0 | 3,50 | 0,20 | 0,10 | 0,5 | 0,60 | ||||||||
| 5,0 | 3,50 | 0,20 | 0,10 | 0,5 | 0,60 | ||||||||
| 5,0 | 3,50 | 0,20 | 8,0 | 1,0 | 0,70 | ||||||||
| 5,0 | 3,50 | 0,20 | 8,0 | 1,0 | 0,70 | ||||||||
| 3,0 | 1,50 | -0,60 | 8,0 | 1,0 | 0,70 | ||||||||
| 3,0 | 1,50 | -0,60 | 8,0 | 1,0 | 0,70 | ||||||||
| 3,0 | 1,50 | -0,60 | 2,0 | 0,50 | 2,0 | 0,81 | |||||||
| 3,0 | 1,50 | -0,60 | 2,0 | 0,50 | 2,0 | 0,81 | |||||||
| 6,0 | 4,50 | 0,50 | 2,0 | 0,50 | 2,0 | 0,81 | |||||||
| 6,0 | 4,50 | 0,50 | 2,0 | 0,50 | 2,0 | 0,81 |
№ - номер вариант (порядковый номер фамилии студента в списке группы), А – номер вопроса для данного варианта.
ВМ 2
ЗАКОНЫНЬЮТОНА
К концам невесомой и нерастяжимой нити, перекинутой через невесомый блок, подвешены грузы: слева n одинаковых тел массой m каждый, соединённых невесомыми нерастяжимыми нитями; справа – груз массой М. Найти:
Œ силу натяжения нити между i и i + 1 телами; построить график Т=f(i);
модуль результирующей силы, действующей на i тело; построить график а = f(i);
Ž модуль результирующей силы, действующей на группу из k тел, расположенных ниже i тела; построить график | R |= f(k);
модуль разности сил натяжения нитей, прикреплённых к группе из k тел, расположенных ниже i тела; построить график | R |= f(k).
Числовые данные
| № | А | М, кг | m, г | n | i | k | № | А | М, кг | m, г | n | i | k |
| 5,0 | 3,0 | ||||||||||||
| 5,0 | 3,0 | ||||||||||||
| 5,0 | 1,5 | ||||||||||||
| 5,0 | 1,5 | ||||||||||||
| 4,0 | 1,5 | ||||||||||||
| 4,0 | 1,5 | ||||||||||||
| 4,0 | |||||||||||||
| 4,0 | |||||||||||||
| 3,5 | |||||||||||||
| 3,5 | |||||||||||||
| 3,5 | |||||||||||||
| 3,5 | |||||||||||||
| 3,0 | |||||||||||||
| 3,0 |
№ – номер варианта (порядковый номер фамилии студента в группе), А – номер вопроса для данного варианта.
ЗАКОНЫСОХРАНЕНИЯ
Пуля массой m, летевшая горизонтально со скоростью v попадает в неподвижно лежащий на горизонтальной поверхности (коэффициент трения между поверхностью и бруском m) брусок массы М. После взаимодействия пули с бруском скорость пули в горизонтальном направлении стала равной k v.
1. Сколько времени t будет двигаться брусок после соударения с пулей?
2. Какое расстояние s будет пройдено бруском после соударения с пулей?
3. Найти относительное изменение кинетической энергии системы пуля-брусок за время соударения.
4. Какую долю e составляет кинетическая энергия бруска от полной кинетической энергии пули и бруска до взаимодействия?
Числовые данные
| № | А | m, г | u м/с | M, кг | m, 10-2 | k | № | А | m, г | u, м/с | M, кг | m 10-2 | k |
| 9,0 | 0,70 | 2,5 | 1 50 | 1,00 | 0,32 | ||||||||
| 9,0 | 0,70 | 2,5 | 1,00 | 0,32 | |||||||||
| 9,0 | 0,70 | 0,10 | 0,5 | -0,6 | |||||||||
| 9,0 | 0,70 | 0,10 | 0,5 | -0,6 | |||||||||
| 4,0 | 2,50 | 0,90 | 0,10 | 0,5 | -0,6 | ||||||||
| 4,0 | 2,50 | 0,90 | 0,10 | 0,5 | -0,6 | ||||||||
| 4,0 | 2,50 | 0,90 | 1,0 | 0,50 | 1,0 | 0,17 | |||||||
| 4,0 | 2,50 | 0,90 | 1,0 | 0,50 | 1,0 | 0,17 | |||||||
| 3,0 | 1,50 | 0,45 | 1,0 | 0,50 | 1,0 | 0,17 | |||||||
| 3,0 | 1,50 | 0,45 | 1,0 | 0,50 | 1,0 | 0,17 | |||||||
| 3,0 | 1,50 | 0,45 | 5,0 | 4,0 | 2,4 | 0,84 | |||||||
| 3,0 | 1,50 | 0,45 | 5,0 | 4,0 | 2,4 | 0,84 | |||||||
| 2,5 | 1,00 | 0,32 | 5,0 | 4,0 | 2,4 | 0,84 | |||||||
| 2,5 | 1,00 | 0,32 | 5,0 | 4,0 | 2,4 | 0,84 |
№ — номер варианта (порядковый номер фамилии студента в списке группы), А – номер вопроса для данного варианта.
АС
ЗАКОНЫНЬЮТОНА
К концам невесомой и нерастяжимой нити, перекинутой через невесомый блок, подвешены грузы: слева n одинаковых тел массой m каждый, соединённых невесомыми нерастяжимыми нитями; справа – груз массой М. Найти:
Œ силу натяжения нити между i и i + 1 телами; построить график Т=f(i);
модуль результирующей силы, действующей на i тело; построить график а = f(i);
Ž модуль результирующей силы, действующей на группу из k тел, расположенных ниже i тела; построить график | R |= f(k);
модуль разности сил натяжения нитей, прикреплённых к группе из k тел, расположенных ниже i тела; построить график | R |= f(k).
Числовые данные
| № | А | М, кг | m, г | n | i | k | № | А | М, кг | m, г | n | i | k |
| 5,0 | |||||||||||||
| 5,0 | |||||||||||||
| 7,0 | |||||||||||||
| 7,0 | |||||||||||||
| 2,7 | 7,0 | ||||||||||||
| 2,7 | 7,0 | ||||||||||||
| 2,7 | 3,5 | ||||||||||||
| 2,7 | 3,5 | ||||||||||||
| 3,9 | 3,5 | ||||||||||||
| 3,9 | 3,5 | ||||||||||||
| 3,9 | 9,9 | ||||||||||||
| 3,9 | 9,9 | ||||||||||||
| 5,0 | 9,9 | ||||||||||||
| 5,0 | 9,9 |
№ – номер варианта (порядковый номер фамилии студента в группе), А – номер вопроса для данного варианта,
ЗАКОНЫСОХРАНЕНИЯ
Пуля массой m, летевшая горизонтально со скоростью v попадает в неподвижно лежащий на горизонтальной поверхности (коэффициент трения между поверхностью и бруском m) брусок массы М. После взаимодействия пули с бруском скорость пули в горизонтальном направлении стала равной k v.
1. Сколько времени t будет двигаться брусок после соударения с пулей?
2. Какое расстояние s будет пройдено бруском после соударения с пулей?
3. Найти относительное изменение кинетической энергии системы пуля-брусок за время соударения.
4. Какую долю e составляет кинетическая энергия бруска от полной кинетической энергии пули и бруска до взаимодействия?
Числовые данные
| № | А | m, г | u, м/с | M, кг | m, 10-2 | k | № | А | m, г | u, м/с | M, кг | m, 10-2 | k |
| 2,0 | 0,50 | -0,80 | 3,5 | 2,50 | -0,06 | ||||||||
| 2,0 | 0,50 | -0,80 | 3,5 | 2,50 | -0,06 | ||||||||
| 2,0 | 0,50 | -0,80 | 0,10 | 0,7 | 0,123 | ||||||||
| 2,0 | 0,50 | -0,80 | 0,10 | 0,7 | 0,123 | ||||||||
| 5,6 | 1,50 | 0,856 | 0,10 | 0,7 | 0,123 | ||||||||
| 5,6 | 1,50 | 0,856 | 0,10 | 0,7 | 0,123 | ||||||||
| 5,6 | 1,50 | 0,856 | 9,0 | 1,00 | 1,0 | -0,77 | |||||||
| 5,6 | 1,50 | 0,856 | 9,0 | 1,00 | 1,0 | -0,77 | |||||||
| 3,0 | 3,50 | -0,93 | 9,0 | 1,00 | 1,0 | -0,77 | |||||||
| 3,0 | 3,50 | -0,93 | 9,0 | 1,00 | 1,0 | -0,77 | |||||||
| 3,0 | 3,50 | -0,93 | 6,50 | 2,7 | -0,14 | ||||||||
| 3,0 | 3,50 | -0,93 | 6,50 | 2,7 | -0,14 | ||||||||
| 3,5 | 2,50 | -0,06 | 6,50 | 2,7 | -0,14 | ||||||||
| 3,5 | 2,50 | -0,06 | 6,50 | 2,7 | -0,14 |
№ – номер варианта (порядковый номер фамилии студента в группе), А – номер вопроса для данного варианта,
Расчётное задание № 2. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
ВМ 1
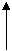
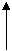
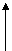
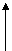
j v0 j v0 j v0 j
i k
oa i о a k o a k o
k a
i i v0
1 вариант 2 вариант 3 вариант 4 вариант
Частице массой m сообщена начальная скорость v 0 под углом a к горизонту. Траектория частицы лежит в одной из координатных плоскостей. Пренебрегая сопротивлением воздуха, найти зависимость от времени t относительно точки бросания О:
· момента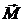 
силы, действующей на частицу;
· момента импульса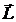 
частицы.
Построить траекторию движения частицы.
Числовые данные
| № | Вариант | m,кг | t,c | a,0 | u0 , м/с | № | Вариант | m,кг | t,c | a,0 | u0,м/с |
| 1,0 | -50 | 4,0 | 1,10 | ||||||||
| 1,0 | 1,9 | -30 | |||||||||
| 2,0 | 0,80 | ||||||||||
| 4,0 | 0,60 | ||||||||||
| 0,10 | 1,00 | ||||||||||
| 0,15 | 4,5 | ||||||||||
| 0,30 | -25 | 3,00 | -210 | ||||||||
| 0,45 | 0,18 | 3,05 | -45 | ||||||||
| 0,05 | 3,10 | ||||||||||
| 1,7 | -10 | 3,2 | 0,17 | ||||||||
| 2,7 | 9,0 | -100 | |||||||||
| 3,7 | -20 | ||||||||||
| 0,50 | 1,20 | 8,21 | 35,5 | ||||||||
| 1,70 | 3,42 | 3,07 |
№ – номер варианта (порядковый номер фамилии студента в группе).
ВМ 2
v0v0 j v0 k v0
k j
o a o a o a o a
i i i i
j k j k
1 вариант 2 вариант 3 вариант 4 вариант
Частице массой m сообщена начальная скорость v 0 под углом a к горизонту. Траектория частицы лежит в одной из координатных плоскостей. Пренебрегая сопротивлением воздуха, найти зависимость от времени t относительно точки бросания О:
· момента 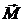силы, действующей на частицу;
· момента импульса 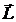частицы.
Построить траекторию движения частицы.
Числовые данные
| № | Вариант | m,кг | t,c | a,0 | u0, м/с | № | Вариант | m,кг | t,c | a,0 | u0, м/с |
| 1 | 0,10 | 3 | 1,8 | ||||||||
| 2 | 0,20 | 4 | 0,95 | ||||||||
| 3 | 0,30 | -100 | 1 | 1,00 | |||||||
| 4 | 0,40 | 2 | 0,60 | -49 | |||||||
| 1 | 0,20 | 3 | |||||||||
| 2 | 0,50 | 4 | -21 | ||||||||
| 3 | 0,70 | 1 | 2,0 | ||||||||
| 4 | 0,15 | -30 | 2 | 6,0 | |||||||
| 1 | 0,30 | 3 | 5,0 | ||||||||
| 2 | 0,70 | 4 | |||||||||
| 3 | 0,50 | 1 | 2,50 | -200 | |||||||
| 4 | 1,1 | 2 | 1,10 | -450 | |||||||
| 1 | 0,40 | 3 | 1,20 | ||||||||
| 2 | 0,55 | -55 | 4 | 1,30 | 3,0 |
№ – номер варианта (порядковый номер фамилии студента в группе).
АС
i v0v0 v0 j v0
j o i o a o a o a
j i
k k j k i k
1 вариант 2 вариант 3 вариант 4 вариант
Частице массой m сообщена начальная скорость v 0 под углом a к горизонту. Траектория частицы лежит в одной из координатных плоскостей. Пренебрегая сопротивлением воздуха, найти зависимость от времени t относительно точки бросания О:
· момента 
силы, действующей на частицу;
· момента импульса 
частицы.
Построить траекторию движения частицы.
Числовые данные
| № | Вариант | m,кг | t,c | a,0 | u0,м/с | № | Вариант | m,кг | t,c | a,0 | u0,м/с |
| 0,10 | 1,8 | ||||||||||
| 0,20 | 0,95 | ||||||||||
| 0,30 | -100 | 1,00 | |||||||||
| 0,40 | 0,60 | -49 | |||||||||
| 0,20 | |||||||||||
| 0,50 | -21 | ||||||||||
| 0,70 | 2,0 | ||||||||||
| 0,15 | -30 | 6,0 | |||||||||
| 0,30 | 5,0 | ||||||||||
| 0,70 | |||||||||||
| 0,50 | 2,50 | -200 | |||||||||
| 1,1 | 1,10 | -450 | |||||||||
| 0,40 | 1,20 | ||||||||||
| 0,55 | -55 | 1,30 | 3,0 |
№ – номер варианта (порядковый номер фамилии студента в группе).