Дано: механическая система (рис. 2.1) состоит из двух твердых тел:
АС и СВ.
Р 1 = 5 кН; Р 2 = 7 кН; М = 22 кН∙м; q = 2 кН/м; α = 60°.
Определить реакции в шарнирах А и В, а также в соединительном шарнире С.
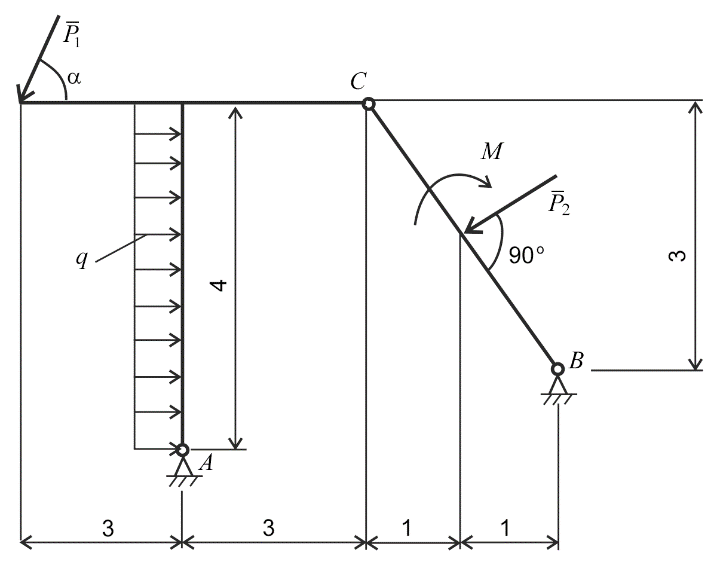
Рис. 2.1. Схема механической системы
Решение
Решение этой задачи можно провести, разделив механическую систему по шарниру С на две.
Выделим объект равновесия – механическую систему, расположенную левее шарнира С (рис. 2.2).
Представим его как свободное тело, мысленно удалив наложенные связи. Приложим в соответствии с условием задачи внешнюю нагрузку, т.е. сосредоточенную силу Р, равномерно распределенную нагрузку заменим равнодействующей Q = q ×(АЕ) = 2×4 = 8 кН (AL = LE = 0,5 AE = 2 м;
АК 1 = ОЕ = 3 м; АК 2 = ЕС = 2 м).

Рис. 2.2. Схемы механической системы: а – объект равновесия находится
левее шарнира; б – действие на систему произвольной системы сил
Вместо удаленных связей в точках А и С приложим составляющие реакций XA, YA, XC, YC.
На механическую систему, приведенную на рис. 2.2, действует плоская произвольная система сил. В данном случае может быть составлено три независимых уравнения равновесия.
Составим уравнения проекций сил на оси x и y, а также уравнение моментов относительно точки А:
å FEix = XA + Q + XC - P 1× cos a = 0; (2.1)
å FEiy = YA + YC - P 1× sin a = 0. (2.2)
Для упрощения вычисления момента силы P 1 относительно точки А разложим ее на горизонтальную (Р 1 х ) и вертикальную (Р 1 y) составляющие:
Р 1 х = P 1× cos a = 5× cos 60° = 5× 0,5 = 2,5 кН;
Р 1 у = P 1× sin a = 5× sin 60° = 5× 0,866 = 4,33 кН.
Момент силы Р 1 относительно точки А определим следующим образом:
МА (Р 1) = МА (Р 1 х ) + МА (Р 1 у ).
å МЕiA = P 1× cos a× АЕ + P 1× sin a× АК 1 - Q× AL - XC × АЕ + YC × АК 2 = 0. (2.3)
После подстановки численных значений уравнения (2.1) - (2.3) получают вид:
ХА + ХС = -5,5 кН; (2.4)
YA + YC = 0,87 кН; (2.5)
3 YC - 4 ХС = 6,99 кН. (2.6)
Система трех алгебраических уравнений (4) - (6) содержит четыре неизвестные и пока разрешена быть не может.
Рассмотрим равновесие механической системы, расположенной правее шарнира С (рис. 2.3), повторяя методику, примененную ранее.
Активная нагрузка приложенная к балке СВ – сосредоточенная сила Р 2, момент М. Реакции связей в точках В и С – ХB, YB, XC', YC'.
В соответствии с аксиомой о равенстве действия и противодействия:
XC = XC'; (2.7)
YC = YC'. (2.8)
Составим уравнения равновесия рассматриваемой механической системы:
å FEix = XВ - P 2× cos (90° - b) - XC' = 0; (2.9)
å FEiy = YВ - P 2×sin (90° - b) - YC' = 0; (2.10)
å МЕiВ = XC¢ × ВК 3 + YC' × О 2 В - М + Р 2× DB = 0; (2.11)

DB = 0,5 CВ = 2,24 м; cos b = О 2 В/СВ = 2/4,47 = 0,45;
sin b = О2 С/СВ = 4/4,47 = 0,89; cos (90° - b) = sin b = 0,89;
sin (90° - b) = cos b = 0,45.
После подстановки численных значений и вычислений получим:
XB - XC' = 6,23 кН; (2.12)
YB - YC' = 3,15 кН; (2.13')
4 XC' + 2 YC' = 6,32 кН. (2.14')
Система шести алгебраических уравнений (2.4) - (2.6), (2.12 ) - (2.14) с учетом равенств (2.7) и (2.8) содержит шесть неизвестных реакций, которые могут быть определены.
Из уравнений (2.6) и (2.14) находим YC = 2,66 кН; XC = (6,32 - 2×2,66)/4 = = 0,25 кН.
Из уравнения (2.5) определим YA = 0,87 - 2,66 = -1,79 кН.
Из уравнения (2.4) можно найти XA = -5,5 - 0,25 = -5,75 кН.
С помощью уравнения (2.12) определим XB = 6,23 + 0,25 = 6,48 кН.
Решая уравнение (2.10), вычислим YB = 3,15 + 2,66 = 5,81 кН.
а) б)

Рис. 2.3. Схемы механической системы: а – объект равновесия находится
правее шарнира; б – действие на систему произвольной системы сил
Для проверки правильности определения реакций убедимся, что соблюдается не использованное ранее уравнение равновесия сил, приложенных ко всей конструкции, например:
å FixE = XA + Q - P 1 x - P 2×cos (90° - b) + XB = 0;
-5,75 + 8 - 2,5 - 7×0,89 + 6,48 @ 0.
Найденные реакции связей:
XA = -5,75 кН, YA = -1,79 кН,
RA =  = 6,02 кН, XB = 6,48 кН, YB = 5,81 кН;
= 6,02 кН, XB = 6,48 кН, YB = 5,81 кН;
RB =  =8,7 кН, XC = 0,25 кН, YC = 2,66 кН;
=8,7 кН, XC = 0,25 кН, YC = 2,66 кН;
RC =  = 2,67 кН.
= 2,67 кН.
Значения реакций связей XA и YA оказались отрицательными, следовательно, их действительные направления противоположны показанным на рис. 2.2.