Вопросы по курсу «Дискретная математика».
Множества. Отношения. Функции
1. Множества (конечные и бесконечные).
Понятие множества нельзя определить через более общие понятия, так как таких понятий в математике нет. Понятие множества является настолько общим, что для него невозможно дать формальное определение. Интуитивно, под множеством понимается совокупность различных объектов, объединенных по какому-то одному или нескольким признаков. Объекты, составляющие множество, называются элементами. Тот факт, что объект x принадлежит множеству A, передается записью x 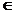 A (читается - “элемент x принадлежит множеству A”).. Если x не является элементом A, то пишут x
A (читается - “элемент x принадлежит множеству A”).. Если x не является элементом A, то пишут x 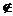 A. Элементы множеств обычно обозначаются строчными латинскими буквами x, y, a, b, c; множества часто обозначают прописными латинскими буквами A, B, C, X, Y.
A. Элементы множеств обычно обозначаются строчными латинскими буквами x, y, a, b, c; множества часто обозначают прописными латинскими буквами A, B, C, X, Y.
Если множество содержит конечное число элементов, то говорят, что оно конечно, в противном случае множество называется бесконечным. Число элементов конечного множества A называется мощностью множества A и обозначается |A|. В дальнейшем мы будем различать общий (текущий) элемент x множества A, т.е. произвольный элемент, характеризующийся единственным свойством “принадлежать множеству A”, и конкретные элементы a, b, c каждый из которых отличен от других. Множество A, состоящее из элементов a,b,c,... записывается A={a,b,c,...}.
Подмножества.
Понятие подмножества возникает тогда, когда необходимо рассматривать некоторое множество не самостоятельно, а как часть другого, более широкого множества.
Множество B называется подмножеством множества A, если всякий элемент множества B является элементом множества A. Запись B 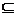 A (не исключает, что B=A).
A (не исключает, что B=A).
Определённое ранее пустое множество по определению является подмножеством любого множества.
По определению пустое множество является конечным.
По определению множество является подмножеством самого себя, A 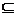 A.
A.
Таким образом, у каждого множества (кроме пустого) есть по крайней мере два подмножества - само множество и пустое.
Важным понятием является понятие подмножества. Понятие подмножества всегда применяется к паре множеств.
Определение
Говорят, что множество А является подмножеством множества В (пишут А  В) тогда и только тогда, когда каждый элемент множества А является элементом множества В.
В) тогда и только тогда, когда каждый элемент множества А является элементом множества В.
Теорема
Для того, чтобы множество А являлось подмножеством множества В, необходимо и достаточно, чтобы A\B = Ø.
Множество всех подмножеств множества А обозначают 2A. Ясно, что Ø  2A и А
2A и А  2A. Они называются несобственными подмножествами множества А. Остальные подмножества (если они есть) называются собственными.
2A. Они называются несобственными подмножествами множества А. Остальные подмножества (если они есть) называются собственными.
Пример
Пусть А = {1,2,3}. Ясно, что 2A = {Ø, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}.
Операции над множествами и их свойства.
Алгебраическими операциями называют такие, при выполнении которых результирующее множество либо пусто, либо состоит из элементов, из которых состоят и множества, подвергающиеся операциям.
Кардинальными операциями называют такие операции, при выполнении которых появляются новые элементы.
Основными алгебраическими операциями над множествами являются следующие:
- пересечение множеств,
- объединение множеств.
-разность множеств.
Пусть А и В - произвольные множества. Их пересечением называется множество
А 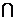 В={x| x
В={x| x 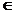 A и x
A и x 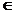 B}.
B}.
Объединением множеств А и В называется множество
А 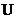 В={x|x
В={x|x 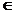 A или x
A или x 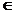 B}.
B}.
Разностью множеств А и В называется множество А\В={x|x 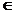 A, но x
A, но x 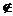 B}.
B}.
Используя понятие универса, можно ввести еще две операции над множествами - дополнение и симметрическую разность множеств.
Дополнением множества А (до универса J) называется множество 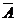 =J\A, т.е.
=J\A, т.е. 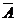 ={x| x
={x| x 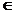 J, но x
J, но x 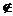 A}.
A}.
Симметрической разностью множеств А и В называется множество
А 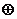 В=(A\B)
В=(A\B) 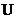 (B\A).
(B\A).
Если А 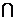 В=
В= 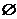 , то говорят, что множества А и В не пересекаются.
, то говорят, что множества А и В не пересекаются.
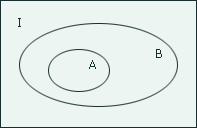
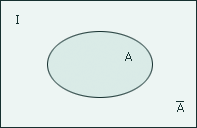
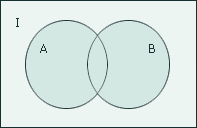
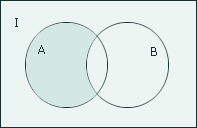
Геометрическое изображение.
Определение
Дополнением ко множеству А относительно универсального множества I называется множество, обозначаемое Ā, определяемое 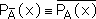
Свойства разности и дополнения:
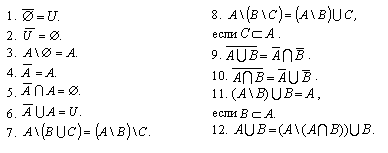
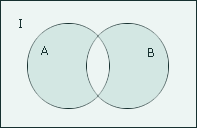
Определение
Объединением множеств А и В называется множество, обозначаемое А  В, определяемое
В, определяемое 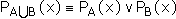
Свойства объединения множеств:
1. 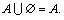
2. 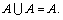
3. 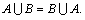
4. 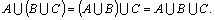
5. 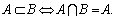
6. 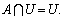
Определение
Пересечением множеств А и В называется множество, обозначаемое А  В, определяемое
В, определяемое 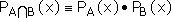
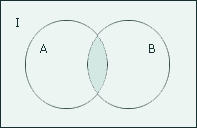
Свойства пересечения множеств:
1. 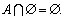
2. 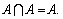
3. 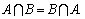
4. 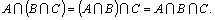
5. 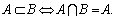
6. 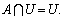
Определение
Разностью множеств А и В называется множество, обозначаемое А\В, (А-В), определяемое 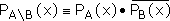
Свойства разности множеств:
1.Если 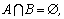 тоА\В=А.
тоА\В=А.
2.ЕслиАÌВ,тоА\В=Æ.
3. А \ В = А \ (А  В).
В).
Имеют место следующие равенства:
1. A\Ø = A.
2. Ø\A = Ø.
3. A\I = Ø.
4. I\A = Ā.
5. A\A = Ø.
Определение
Симметрической разностью множеств А и В называют множество, обозначаемое АΔВ (А―В), определяемое AΔB ≡ (A\B)  (B\A).
(B\A).
Имеет место равенство:
AΔB = (A  B)\(A
B)\(A  B)
B)
Имеют место следующие равенства:
1. АΔВ = BΔA – коммутативность.
2. АΔI = Ā.
АΔØ = A.
Способы задания множеств.
Способы задания множеств.
1. Перечислением своих элементов.
A={a,b,c,...}.
2. Через описание ограничительного свойства.
A={x| P(x)} - A множество таких элементов x, которые обладают свойством P(x).
В дальнейшем мы будем пользоваться общепринятыми обозначениями множеств:
N - множество натуральных чисел,
Z - множество целых чисел,
Q - множество рациональных чисел,
C - множество комплексных чисел,
R - множество действительных чисел,
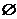 - пустое множество.
- пустое множество.
Универсальное множество. (?)
Истинным, строгим или собственным подмножеством множества А называется такое его подмножество В, что В 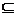 А и В
А и В 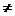 А. Запись В
А. Запись В 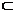 А, где
А, где 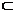 - знак строгого включения.
- знак строгого включения.
По отношению к множеству А - пустое множество и само множество А называется несобственным, нестрогим или не истинным подмножествами множества А.
Таким образом, мы имеем следующие свойства множеств:
1. А 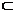 В
В 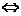 А
А 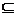 В и А
В и А 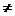 В.
В.
2. А 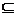 В
В 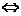 А
А 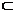 В или А=В.
В или А=В.
3. А 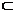 В
В 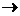 А
А 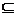 В.
В.
4. А 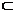 В
В 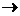 А
А 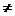 В.
В.
5. А 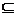 В и В
В и В 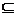 С
С 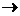 А
А  С.
С.
6. А 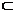 В и В
В и В  С
С 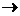 А
А 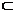 С.
С.
7. А 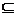 В и В
В и В 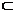 С
С 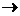 А
А 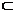 С.
С.
Первые четыре свойства следуют из введенных ранее определений.
Покажем выполнение остальных свойств.
Свойство 5.
Докажем его методом от противного.
Пусть А 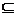 В и В
В и В 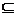 С но А
С но А 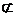 С и А
С и А 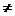 С.
С.
Тогда существует такой элемент а 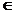 А, но а
А, но а 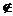 С. Тогда, т.к. В
С. Тогда, т.к. В 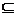 С, то а
С, то а 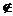 В.
В.
Получили противоречие: а 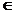 А, а
А, а 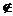 В, но А
В, но А 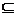 В.
В.
Свойство 6.
Так как А 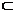 В и В
В и В 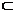 С, то по свойству 3 А
С, то по свойству 3 А 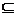 В и В
В и В 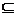 С и по свойству 5 А
С и по свойству 5 А 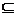 С. Осталось показать, что А
С. Осталось показать, что А 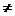 С. Пусть это не так и А=С. Т.е. для любого элемента а, а
С. Пусть это не так и А=С. Т.е. для любого элемента а, а 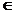 А
А 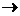 а
а 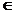 С. Так как В
С. Так как В 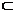 С, то В
С, то В 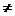 С и найдется элемент в,в
С и найдется элемент в,в 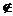 В., но в
В., но в 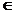 С. Так как А
С. Так как А 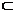 В, то в
В, то в 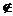 А. Отсюда элемент в присутствует в множестве С, но отсутствует в множестве А, отсюда эти множества не равны.
А. Отсюда элемент в присутствует в множестве С, но отсутствует в множестве А, отсюда эти множества не равны.
Свойство 7.
Так как В 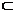 С, то по свойству 3 В
С, то по свойству 3 В 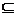 С и тогда по свойству 5 А
С и тогда по свойству 5 А 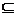 С. Осталось показать, что А
С. Осталось показать, что А 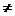 С. Действительно, так как В
С. Действительно, так как В 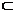 С, то найдется элемент а, а
С, то найдется элемент а, а 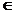 С, но а
С, но а 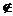 В. Так как А
В. Так как А 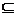 В, то а
В, то а 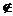 А. Отсюда а
А. Отсюда а 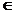 С, но а
С, но а 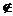 А, т.е. А
А, т.е. А 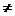 С.
С.
Если все рассматриваемые в ходе рассуждений множества являются подмножествами некоторого фиксированного множество J, то это множество называют универсальным(для рассматриваемого набора множеств ) множеством или универсом. Таким образом, универс - это такое множество,что любоерассматриваемое множество является его подмножеством.
Рассмотрим множество А={a,b,c}. Найдем все его различные подмножества. Это: пустое множество 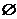 , три одноэлементных подмножества {a}, {b}, {c}, три двухэлементных подмножества {a,b}, {a,c}, {b,c} и одно трёхэлементное множества - само множество А. Множество всех подмножеств множества А будем обозначать как P(A) или
, три одноэлементных подмножества {a}, {b}, {c}, три двухэлементных подмножества {a,b}, {a,c}, {b,c} и одно трёхэлементное множества - само множество А. Множество всех подмножеств множества А будем обозначать как P(A) или 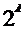 .
.
Характеристическая функция множества.
Характеристической функцией ХA множества А называется одноместная функция, равная 0 на элементах множества А и 1 за пределами А. Характеристическая функция называется частичной, если она не определена за пределами А. Множество А называется примитивно рекурсивным, если его характеристическая функция примитивно рекурсивна. Множество А называется частично рекурсивным, если его характеристическая функция частично рекурсивна.
Множество А называется рекурсивно перечислимым, если существует двухместная частично рекурсивная функция ƒ(a,x) такая, что уравнение ƒ(a,x) = 0 имеет решение тогда и только тогда, когда а Î А.
Задачу кластеризации удобно формулировать использую характеристическую функцию. Характеристическая функция может принимать два значения: 0 - если элемент не принадлежит кластеру, и 1 - если элемент принадлежит кластеру. Используя характеристическую функцию, опишем кластеры следующей матрицей разбиения:
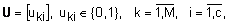 ,
,
где k-ая строчка матрицы 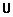 указывает на принадлежность объекта
указывает на принадлежность объекта 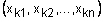 к кластерам
к кластерам 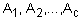 .
.
Матрица 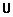 должна обладать следующими свойствами:
должна обладать следующими свойствами:
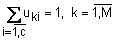 ; (12.4)
; (12.4)
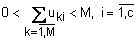 ; (12.5)
; (12.5)
Для оценки качества разбиения используется критерий разброса, показывающий сумму расстояний от объектов до центра своего кластера. Для евклидового пространства этот критерий записывается так [1]:
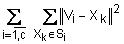 ; (12.6)
; (12.6)
где 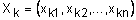 - к-й объект кластеризации;
- к-й объект кластеризации;
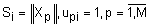 - i-й кластер;
- i-й кластер;
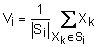 - центр i-го кластера.
- центр i-го кластера.
Кластеризацию объектов 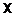 можно сформулировать как следующую задачу оптимизации: найти матрицу
можно сформулировать как следующую задачу оптимизации: найти матрицу 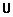 , минимизирующую значение критерия (12.6). Дискретный характер четкого разбиения приводит к трудностям нахождения оптимальной кластеризации из-за негладкости целевой функции.
, минимизирующую значение критерия (12.6). Дискретный характер четкого разбиения приводит к трудностям нахождения оптимальной кластеризации из-за негладкости целевой функции.
Булеан.
Пусть А произвольное конечное n- элементное множество. Найдем мощность множества P(A), |P(А)|= 
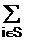
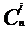 , где S={0,1,...,n}.
, где S={0,1,...,n}.
Для определения величины |Р(А)| воспользуемся формулой бинома Ньютона.
 , при условиях, что a=в=1.
, при условиях, что a=в=1.
Получаем,  =|P(A)|.
=|P(A)|.
Замечание.
Множество 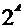 называется булеаном множества А.
называется булеаном множества А.
2. Декартово произведение.
Кардинальными операциями называются такие операции, при применении которых в результирующем множестве появляются новые элементы.
Примером кардинальных операция является прямое (декартово) произведение множеств.
Прямым произведением множеств А и В называется множество
А 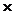 В={(a,b)| a
В={(a,b)| a 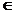 A, b
A, b 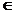 B}, т.е. множество тех и только тех пар, первая компонента которых принадлежит множеству А, а вторая В.
B}, т.е. множество тех и только тех пар, первая компонента которых принадлежит множеству А, а вторая В.
Через 
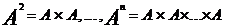 - обозначают, соответственно, декартов квадрат и декартову n-ую степень множества А.
- обозначают, соответственно, декартов квадрат и декартову n-ую степень множества А.
Отношения (рефлексивности, симметричности, асимметричности, антисимметричности, транзитивности, антитранзитивности) и их свойства.
Отношения эквивалентности.
3. Функция - отображение.
Отношение f на AxB называется функцией из A в B 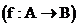 , если
, если 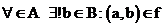
если это отображение 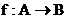 является функцией и выполняется условие
является функцией и выполняется условие 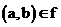 , то говорят, что
, то говорят, что 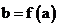
-если 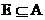 , то функция
, то функция 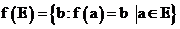 (f – образ множества A)
(f – образ множества A)
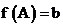 - множество значений
- множество значений
Биекция.
-отображение 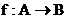 называется инъективным (инъекция), если из того, что
называется инъективным (инъекция), если из того, что 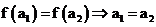 называется отображением “на”
называется отображением “на”
-называется сюръективным, если для любых 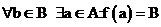
-отображение f называется взаимооднозначным или биекцией, если это отображение является и инъективным и сюръективным
если для любого  и
и 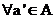 :
: 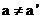
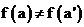
- 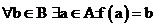
если A=B, то эти отображения называются перестановкой в множестве A.
Эквивалентность множеств.
Счетные множества.
Счетным множеством называется всякое множество, элементам которого можно поставить во взаимно однозначное соответствие множество натуральных чисел.
Отсюда, счетное множество - это бесконечное множество, элементы которого можно перенумеровать натуральными числами.
Примерами счетных множеств, кроме множества натуральных чисел, являются:
- множество целых чисел Z,
- множество всех четных положительных (отрицательных) чисел,
- множество натуральных степеней числа 2,
- множество рациональных чисел Q,
- множество алгебраических чисел и т.д.
Покажем, например, счетность множества алгебраических чисел.
Число а называется алгебраическим, если оно является корнем некоторого многочлена с целыми коэффициентами.
Так как множество целых чисел счетно, то занумеруем их, например, следующим образом:
если целое число n неотрицательно,
то поставим ему в соответствие номер 2n+1, (1)
если целое число n отрицательное,
то поставим ему в соответствие номер 2|n|.
Каждому уравнению вида:
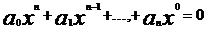 (2)
(2)
поставим в соответствие натуральное число:
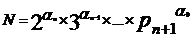 , где 2,3,...,p - простые числа, а
, где 2,3,...,p - простые числа, а 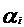 - номер целого числа
- номер целого числа 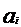 (коэффициента уравнения (1)), полученного после приведенной нумерации (1).
(коэффициента уравнения (1)), полученного после приведенной нумерации (1).
Таким образом можно перенумеровать все уравнения типа (2). Так как каждое уравнение (2) имеет не более n различных корней, то тем самым доказывается счетность множества алгебраических чисел.