Тройные интегралы
- Основные понятия и определения.
Обобщением определенного интеграла на случай функции трех переменных является тройной интеграл от функции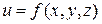 
по области 
:
.
Здесь 
– элемент объема.
Теорема (достаточное условие интегрируемости). Если функция 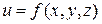непрерывна в ограниченной замкнутой области , то она интегрируема в этой области.
Вычисление тройного интеграла в декартовых координатах
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.
Пусть областью интегрирования является тело, ограниченное снизу поверхностью 
, сверху – поверхностью 
. Функции и (
) полагаемнепрерывными в замкнутой области 
, являющейся проекцией тела на плоскость 
. Будем считать область правильной в направлении оси 
(
простой): любая прямая, параллельная оси , пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области функции 
имеет место формула
(1)
сводящая вычисление тройного интеграла к вычислению двойного интеграла от однократного. При этом сначала вычисляется внутренний интеграл по переменной 
при постоянных 
и 
в пределах изменения . Нижней границей интеграла является аппликата точки входа прямой, параллельной оси , в область , т. е. ; верхней границей – аппликата точки выхода этой прямой из области , т. е. . Результат вычисления этого интеграла есть функция двух переменных и .
Пусть область ограничена с боков линиями 
, 
, 
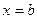, сверху и снизу линиями 
и 
, где 
< 
,– непрерывные на отрезке 
функции. Тогда, переходя от двойного интеграла по области к повторному, получаем формулу сведения тройного интеграла к трехкратному:
. (2)
Замечания.
1. Если область V более сложная, чем рассмотренная, то ее следует разбить на конечное число таких правильных областей, к которым можно применить эту формулу.
2. Порядок интегрирования, при определенных условиях, может быть иным.
Пример1. Вычислить интеграл 
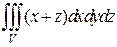, где область ограничена плоскостями
, 
, 
, 
.
Решение. Область является правильной в направлении оси (и в направлении двух других осей ). Ее проекция на плоскость (треугольник)может бытьопределена неравенствами 
. Это правильная в направлении оси 
. По формуле (2) запишем:
. ☻
Задания для самостоятельной работы.
1. Вычислить интеграл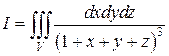 
, тело ограничено координатными плоскостями и плоскостью 
. Ответ.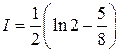 
.
2.. Вычислить интеграл 
, тело ограничено плоскостями 
и поверхностью 
. Ответ. 
.
Замена переменных в тройном интеграле.
Вычисление тройного интеграла
в цилиндрических и сферических координатах
При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т. е. совершается преобразование переменных.
Пусть 
и якобиан преобразования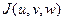 
отличен от нуля.
Формула замены переменных в тройном интеграле имеет вид:
. (1)
Для вычисления тройного интеграла часто используют цилиндрические координаты, связанные с ее декартовыми координатами соотношениями:
(
, 
, 
).Якобиан преобразования 
. Формула перехода к цилиндрическим координатам принимает вид
. (2)
К цилиндрическим координатам удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.
Пример 1. Вычислить интеграл 
, где 
– область, ограниченная верхней частью конуса 
и плоскостью 
.
Решение. Перейдем к цилиндрическим координатам.Уравнение конуса в цилиндрических координатах принимает вид 
.Область интегрирования проектируется на плоскость 
в круг 
, в полярных координатах – 
. Новые переменные изменяются в пределах: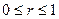 
, , 
.
По формуле (2) запишем: 
. ☻
Сферические координаты связаны с декартовыми координатами 
соотношениями:
(
, , 
). Якобиан перехода к сферическим координатам равен 
и формула перехода к сферическим координатам принимает вид
. (3)
Переходить к сферическим координатам удобно, когда область интегрирования есть шар (уравнение его границы 
в сферических координатах имеет вид 
)или его часть, а также если подынтегральная функция имеет вид 
.
Пример2. Вычислить интеграл 
, где – шар
.
Решение. Переходим к сферическим координатам.Граница области – сфера, ее уравнение в сферических координатах имеет вид 
. Подынтегральная функция после замены переменных примет вид 
. Новые переменные изменяются в следующих пределах:
(, , ).
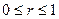По формуле (3) запишем:
. ☻
Пример3. Тело ограничено поверхностью 
и плоскостями 
(цилиндрический отрезок). Найти объём тела.
Решение. Объём находим по формуле 
.
Тело проектируется на плоскость в круг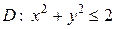 
. Снизу оно ограничено плоскостью 
, сверху – плоскостью 
, с боков – цилиндрической поверхностью . Перейдем к цилиндрическим координатам. Новые переменные 
изменяются соответственно в пределах
Вычислим 
.
Значит, 
.