ДЛЯ КОМПЛЕКСА СОБАЧЬИХ УПРЯЖЕК»

НАУЧНЫЙ ОТЧЕТ ПО ТЕМЕ

 

«ОБОСНОВАНИЕ ПАРАМЕТРОВ УПРУГИХ ПРЕДОХРАНИТЕЛЬНЫХ ДЕМПФЕРОВ-АМОРТИЗАТОРОВ

ДЛЯ КОМПЛЕКСА СОБАЧЬИХ УПРЯЖЕК»

 

«УТВЕРЖДАЮ»

проректор по научной работе и международным связям

ФГБОУ ВПО «ТвГТУ»

доктор технических наук, профессор Зюзин Б.Ф.

 

 

Ответственный исполнитель:

доктор технических наук, доцент Яблонев А.Л.

 

 

Тверь 2013

 

ВВЕДЕНИЕ

 

Актуальность работ по поиску решений и обоснованию параметров демпферов-амортизаторов для собачьих упряжек вызвана необходимостью предохранения от гибели и тяжелых телесных повреждений ездовых собак в результате гонок и катаний на повозках по пересеченной местности. Поскольку этот вид спорта и развлечений уже завоевал своих приверженцев, развивается и приумножается, множатся и травмы, вызванные воздействием упряжи на тела собак. Защита ездовых собак от пиковых нагрузок при проведении заездов возможна при помощи использования упругого демпфера-амортизатора, установленного между колесным картом (нартами) и упряжью собаки. Поискам решений такой конструктивной доработки и обоснованию ее параметров посвящен нижеследующий научный отчет, выполненный представителями ФГБОУ ВПО «Тверской государственный технический университет» по запросу мастера спорта международного класса по гонкам на упряжках Сергея Юрьевича Панюхина – одного из самых известных гонщиков России.

Несколько фактов из истории.

Семья Панюхиных – Елена, Сергей, Дарья, Александра – профессионально занимаются ездовым спортом. В 1992 году на Камчатке они создали первый в России питомник спортивных ездовых собак "Ингляу", который на сегодняшний день лучший в России. С 1997 года семья Панюхиных занимается организацией соревнований. На Камчатке они организовали и провели первые в стране этапы Кубка Европы и Мира по средним дистанциям – гонку "Камчадал" (2004 и 2005 годы), этап Кубка Европы по ски-джорингу (лыжник + собака – 2006 год), готовили гонку "Урал-рейс" в Челябинской области (2007 год).

В 2008 году Панюхины переехали в Центральную Россию, полностью перевезли питомник. Сейчас они располагаются в Тверской области, у них 25 спортивных собак. По словам Сергея Панюхина, в России, к сожалению, к гонкам на собаках до сих пор относятся как к экзотике и занятию чудаков, несмотря на то, что ездовой спорт чрезвычайно развит во всем мире – только в Европе в год проводится около 1000 стартов. Однако наблюдается положительная тенденция: увеличивается количество россиян, занимающихся ездовым спортом, гонки на собаках включены в реестр официальных видов спорта России, проводятся Чемпионаты страны.

Сергей Панюхин о ездовом спорте:

«Это удивительный спорт, думаю единственный, где человек и животные работают вместе на одну цель. В отличие от лошадей, спортивные собаки бегут без принуждения. У них есть кураж и азарт, и настрой на победу. Человек здесь тренер и руководитель, а собаки – члены его спортивной команды, и они рвутся на дистанцию» [1].

Проведенное исследование позволило выявить три наиболее распространенных вида прицепных повозок: трех и четырехколесные карты (для осеннее-весенне-летних заездов) и нарты (для зимних заездов). Для каждой из этих повозок рассмотрено несколько режимов, обобщение которых приводит к параметрам и конструкции демпфера-амортизатора.

1. ТРЕХКОЛЕСНЫЙ ПРИЦЕПНОЙ КАРТ

Трехколесный карт, изображенный на рис. 1. представляет собой прицепную трехколесную повозку, оснащенную устройством управления направлением движения (вращающаяся передняя вилка) и колодочными тормозами всех колес, имеющими механический привод от рычагов, расположенных на руле. Сцепление с собачьей упряжью происходит с помощью потяга, жестко прикрепленного к раме.

 

Рис. 1. Трехколесный карт

 

Собственная масса карта m _к = 25 кг. Максимальная скорость движения V_max = 45 км/ч =12,5 м/с. Средняя скорость движения V_ср = 33 км/ч = 9,17 м/с. Средняя масса наездника принимается m_ч = 80 кг. Геометрические размеры колес приведены на рис. 2. Масса переднего колеса m₁ = 2,3 кг, масса заднего колеса m₂ = 2,0 кг. Общий вес G карта с наездником составляет:

G = (m_к+m_ч)g, (1.1)

где g =9,81 м/с² – ускорение свободного падения.

G = (25 + 80)*9,81 = 1030,05 Н.

 

 

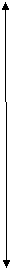
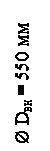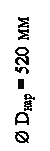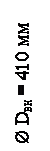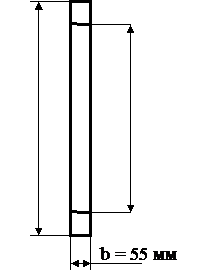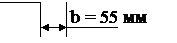а б

Рис. 2. Геометрические размеры колес трехколесного карта:

а – переднее колесо; б – заднее колесо

 

1.1. РАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ ТРЕХКОЛЕСНОГО КАРТА В УПРЯЖКЕ

 

V

T11

При равномерном движении по прямой, на карт действуют следующие силы, изображенные на рис. 3: G – вес карта с наездником; R_д – сила сопротивления передвижению карта; Т₁₁ – толкающая сила, воздействующая на карт через потяг от упряжи собак.

 

 

 

Рис. 3. Силы, действующие на трехколесный карт при прямолинейном равномерном движении

 

Уравнение движения имеет вид:

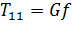, (1.2)

где f – коэффициент сопротивления движению колесных экипажей, принима-емый от 0,05 (для грунтовых дорог) до 0,3 (для песчаных дорог) [2, стр. 17].

С учетом найденного значения G получим формулу для данного случая:

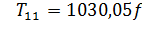. (1.3)

Подставляя f, получим результаты вычислений и сведем их в таблицу 1.1.

Таблица 1.1

f	0,05	0,3
T11, Н	51,5	309,02

 

 

1.2. РАВНОЗАМЕДЛЕННОЕ ДВИЖЕНИЕ ТРЕХКОЛЕСНОГО КАРТА НА ПОДЪЕМЕ В ГОРУ

 

T12

Будем считать, что угол подъема не превышает α = 25^о [опыт заездов]. Схема сил, действующих на карт изображена на рис. 4.

 

 

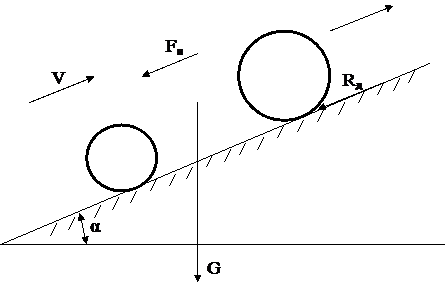
Рис. 4. Силы, действующие на трехколесный карт при равномерном движении в гору

 

Кроме уже перечисленных в п. 1.1, на карт действует сила инерции F_и, вызванная полной массой карта и маховыми моментами вращающихся колес.

Уравнение движения в этом случае имеет вид:

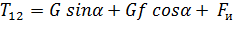. (1.4)

Сила инерции определяется коэффициентом учета вращающихся масс δ_вр, массой экипажа (m_к + m_ч), и замедлением a [2, стр.21], [3, стр. 268]:

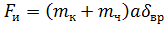. (1.5)

Замедление рассчитать невозможно из-за недостаточности данных об условиях заезда, поэтому оно условно принимается в расчетах a ≈ 1 м/с².

Коэффициент учета вращающихся масс определяется суммарным моментом инерции вращающихся колес J_к, средним радиусом качения колес r_ср и массой экипажа (m_к + m_ч) [3, стр. 268]:

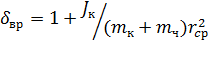. (1.6)

Суммарный момент инерции вращающихся колес J_к определяется моментами инерции всех колес:

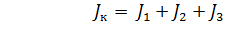, (1.7)

при этом момент инерции одного колеса находится по массе колеса m_J и его геометрическим размерам, как для полого круглого цилиндра [4, стр. 327]:

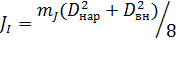. (1.8)

Для переднего колеса: 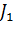= 2,3(0,66²+0,55²)/8 = 0,21 кг*м².

Для заднего колеса: 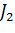= = 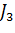2,0(0,52² + 0,41²)/8 = 0,11 кг*м².

Суммарный момент инерции вращающихся колес J_к = 0,21+0,11+0,11=0,43 кг*м².

Средний радиус качения колес трехколесного карта: r_ср = (0,66+0,52+0,52)/3*2 = 0,28 м.

Тогда коэффициент учета вращающихся масс δ_вр = 1+0,43/(80+25)*0,28²=1,05, и сила инерции F_и = (80+25)*1*1,05 = 110,25 Н.

Подставляя в (1.4) все найденные величины и угол подъема, имеем:

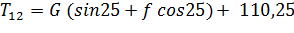= 1030,05*(0,42 + 0,91 f) + 110,25. (1.9)

Подставляя в (1.9) вышеуказанные значения f, получим данные, из которых составим таблицу 1.2.

Таблица 1.2

f	0,05	0,3
T12, Н	587,7	824,1

 

 

1.3. ПРЯМОЛИНЕЙНОЕ РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ ТРЕХКОЛЕСНОГО КАРТА

 

В отличие от случая, описанного в п. 1.1, на карт при прямолинейном движении с ускорением, действует сила инерции 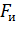, вызванная вращением колес, имеющих маховые массы, и направленная против направления движения (рис. 5).

Т13

Fи

V

 

Рис. 5. Силы, действующие на трехколесный карт при прямолинейном равноускоренном движении

 

Уравнение движения будет иметь вид:

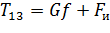. (1.10)

Коэффициент сопротивления передвижению f определен в п. 1.1, сила инерции 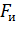в п. 1.2. Таким образом, уравнение (1.10) преобразуется:

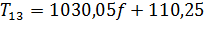. (1.11)

Подставляя в (1.11) значения коэффициента сопротивления передвижению f получим значения 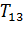, которые занесем в табл. 1.3.

Таблица 1.3

f	0,05	0,3
T13, Н	161,75	419,27

 

 

1.4. ДВИЖЕНИЕ ТРЕХКОЛЕСНОГО КАРТА НА СПУСКЕ ПРИ ТОРМОЖЕНИИ

 

α

Rд

Fи

T14

G

Fт

V

При движении на спуске, гонщик начинает притормаживать (или, даже, тормозить!) всеми тормозами карта, от чего возникает тормозная сила F_т, направленная противоположно скорости движения. Кроме того, сила инерции 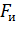, обусловленная вращением колес, имеющих маховые массы, направлена не противоположно, а в одну сторону с вектором скорости движения (рис. 6).

 

 

Рис. 6. Силы, действующие на трехколесный карт при торможении на спуске с горы

 

Уравнение движения в данном случае имеет вид:

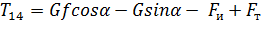. (1.12)

Максимальное значение тормозной силы, принимаемое в расчетах равно силе сцепления между колесом и дорогой:

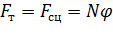, (1.13)

где N – реакция вертикальной нагрузки на колесо; φ – предельный коэффициент сцепления между колесом и дорогой, принимаемый в расчетах

φ = 0,7 [2, стр. 389].

Вертикальная нагрузка на колеса:

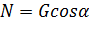. (1.14)

Подставляя все элементы в (1.12), получим:

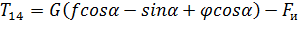, (1.15)

или:

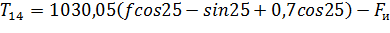, (1.16)

с учетом 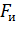и значений тригонометрических функций:

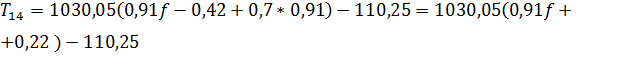. (1.17)

Решая уравнение (1.17) относительно f, найдем значения Т₁₄ и заполним таблицу 1.4.

Таблица 1.4

f	0,05	0,3
T14, Н	163,23	397,56

 

 

1.5. СТОЛКНОВЕНИЕ ТРЕХКОЛЕСНОГО КАРТА, ДВИЖУЩЕГОСЯ ПРЯМОЛИНЕЙНО НА СКОРОСТИ С ПРЕПЯТСТВИЕМ

 

Для оценки этого случая необходимо воспользоваться теоремой об изменении количества движения материальной точки: «Изменение проекции количества движения точки на какую-либо ось равно проекции на ту же ось импульса силы, действующей на точку за то же время» [4, стр. 298]. Математически данная теорема записывается следующим образом:

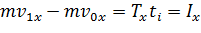, (1.18)

где m – масса тела, сталкивающегося с препятствием, кг; 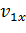– проекция скорости поступательного движения тела на ось ОХ после столкновения с препятствием, м/с; 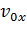– проекция скорости поступательного движения тела на ось ОХ до столкновения с препятствием, м/с; 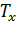– проекция на ось ОХ силы, действующей на тело в процессе столкновения с препятствием (ударом), Н; 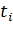– время столкновения с препятствием (удара), с; 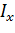– проекция на ось ОХ импульса силы, действующей на тело при столкновении с препятствием.

Время удара в данных условиях определить невозможно из-за ограниченности данных о материале, форме и способе закрепления в почве препятствия, угле наезда на него, характеристиках движения и т.д., поэтому можно ориентировочно принять время удара 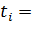0,1 с. Практика разбора аварийных ситуаций на автомобильном транспорте показывает, что при скоростях тела выше 80 км/ч время удара принимается до 0,01 с. Считая удар о препятствие неупругим (иное трудно себе представить, ведь не с резиновой же стеной сталкивается карт!), можно принять также, что 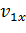= 0, т.е. столкнувшись с препятствием, карт останавливается. Для этих условий можно записать, пользуясь (1.18):

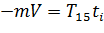, (1.19)

где V – скорость поступательного движения карта до удара (в нашем случае она принимает значение средней V_ср или максимальной скоростей V_max, м/с); 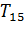– сила, действующая на собак через упряжь со стороны резко и внезапно остановленного карта, Н. Знак «– «показывает, что импульс силы направлен противоположно направлению скорости поступательного движения карта до удара.

Таким образом,

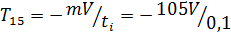. (1.20)

Подставляя в формулу (1.20) значения средней и максимальной скоростей, получим силу, действующую на собак в процессе столкновения с препятствием, которую занесем в таблицу 1.5.

Таблица 1.5

V, м/с	9,17	12,5
Т15, Н	9628,5

 

 

2. ЧЕТЫРЕХКОЛЕСНЫЙ ПРИЦЕПНОЙ КАРТ

 

Четырехколесный карт, изображенный на рис. 7 и 8 представляет собой прицепную четырехколесную повозку, оснащенную устройством управления направлением движения (вращающийся рулевой вал с приводом на оси передних колес) и барабанными тормозами всех колес, имеющими механический привод от рычагов, расположенных на руле. Сцепление с собачьей упряжью происходит с помощью потяга, жестко прикрепленного к раме.

Рис. 7. Четырехколесный прицепной карт

Рис. 8. Четырехколесный прицепной карт (вид сбоку)

 

Собственная масса карта m _к = 35 кг. Максимальная скорость движения V_max = 50 км/ч =13,89 м/с. Средняя скорость движения V_ср = 33 км/ч = 9,17 м/с. Средняя масса наездника принимается m_ч = 80 кг. Геометрические размеры всех четырех одинаковых колес приведены на рис. 9. Масса колеса m₁ = 2,0 кг.

 

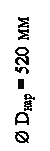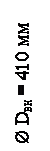Рис. 9. Геометрические размеры колес четырехколесного карта

Общий вес G карта с наездником составляет:

G = (m_к+m_ч)g, (2.1)

где g =9,81 м/с² – ускорение свободного падения.

G = (35 + 80)*9,81 = 1128,15 Н.

 

2.1. РАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ ЧЕТЫРЕХКОЛЕСНОГО КАРТАВ УПРЯЖКЕ

 

При равномерном движении по прямой, на карт действуют следующие силы, изображенные на рис. 10: G – вес карта с наездником; R_д – сила сопротивления передвижению карта; Т₂₁ – толкающая сила, воздействующая на карт через потяг от упряжи собак.

 

Рис. 10. Силы, действующие на четырехколесный карт при прямолинейном равномерном движении

 

Уравнение движения имеет вид:

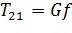, (2.2)

где f – коэффициент сопротивления движению колесных экипажей, принима-емый от 0,05 (для грунтовых дорог) до 0,3 (для песчаных дорог) [2, стр. 17].

С учетом найденного значения G получим формулу для данного случая:

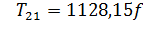. (2.3)

Подставляя f, получим результаты вычислений и сведем их в таблицу 2.1.

 

 

Таблица 2.1

f	0,05	0,3
T21, Н	56,41	338,45

 

 

2.2. РАВНОЗАМЕДЛЕННОЕ ДВИЖЕНИЕ ЧЕТЫРЕХКОЛЕСНОГО КАРТА НА ПОДЪЕМЕ В ГОРУ

 

Будем считать, что угол подъема не превышает α = 25^о [опыт заездов]. Схема сил, действующих на карт изображена на рис. 11.

 

Рис. 11. Схема сил, действующих на четырехколесный карт при равнозамедленном движении в гору

 

Уравнение движения в этом случае имеет вид:

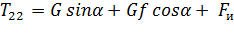. (2.4)

Сила инерции F_и [2, стр. 21], [3, стр. 268], по аналогии с п. 1.2:

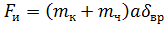. (2.5)

Из-за невозможности расчетов ввиду отсутствия конкретных данных, замедление условно принимается a ≈ 1 м/с².

Коэффициент учета вращающихся масс определяется суммарным моментом инерции вращающихся колес J_к, средним радиусом качения колес r_ср и массой экипажа (m_к + m_ч) [3, стр. 268]:

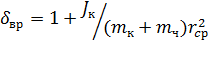. (2.6)

Суммарный момент инерции четырех одинаковых вращающихся колес J_к определяется моментами инерции всех колес:

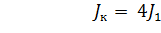, (2.7)

при этом момент инерции одного колеса находится по массе колеса m₁ и его геометрическим размерам, как для полого круглого цилиндра [4, стр. 327]:

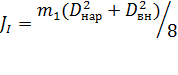. (2.8)

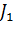= 2,0(0,52²+0,41²)/8 = 0,11 кг*м².

Суммарный момент инерции вращающихся колес J_к = 4*0,11 = 0,44 кг*м².

Средний радиус качения колес четырехколесного карта: r_ср = 0,52/2 = 0,26 м.

Коэффициент учета вращающихся масс δ_вр = 1+0,44/(80+35)*0,26²=1,06 и сила инерции F_и = (80+35)*1*1,06 = 111,3 Н.

Подставляя в (2.4) все найденные величины и угол подъема, имеем:

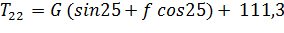= 1128,15*(0,91 f + 0,42) + 111,3. (2.9)

Подставляя в (2.9) вышеуказанные значения f, получим данные, из которых составим таблицу 2.2.

Таблица 2.2

f	0,05	0,3
T22, Н	636,45	893,1

 

 

2.3. ПРЯМОЛИНЕЙНОЕ РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ ЧЕТЫРЕХКОЛЕСНОГО КАРТА

 

На карт в этом случае действуют силы, изображенные на рис. 12.

 

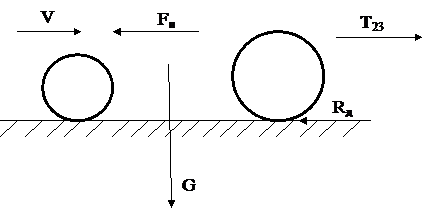Рис. 12. Схема сил, действующих на четырехколеный карт при прямолинейном равноускоренном движении

 

Подобный случай описан в п. 1.3. Уравнение движения имеет вид:

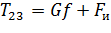. (2.10)

Коэффициент сопротивления передвижению f определен в п. 2.1, сила инерции 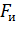в п. 2.2. Таким образом, уравнение (2.10) преобразуется:

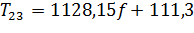. (2.11)

Подставляя в (2.11) значения коэффициента сопротивления передвижению f получим значения 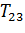, которые занесем в табл. 2.3.

Таблица 2.3

f	0,05	0,3
T23, Н	167,71	449,75

 

 

2.4. ДВИЖЕНИЕ ЧЕТЫРЕХКОЛЕСНОГО КАРТА НА СПУСКЕ ПРИ ТОРМОЖЕНИИ

 

Случай и особенности действия сил на карт описаны в п. 1.4, схема сил представлена на рис. 13.

 

 

 

 

Рис. 13. Силы, действующие на четырехколесный карт на спуске с горы при торможении

 

Уравнение движения в данном случае имеет вид:

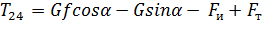. (2.12)

Максимальное значение тормозной силы, принимаемое в расчетах равно силе сцепления между колесом и дорогой (1.13). Вертикальная нагрузка на колеса (1.14).

Подставляя все элементы в (2.12), получим:

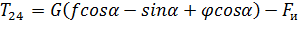, (2.13)

или:

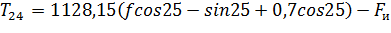, (2.14)

с учетом 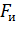и значений тригонометрических функций:

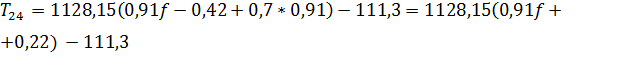. (2.15)

Решая уравнение (2.15) относительно f, найдем значения Т₂₄ и заполним таблицу 2.4.

Таблица 2.4

f	0,05	0,3
T24, Н	188,22	444,87

 

2.5. СТОЛКНОВЕНИЕ ЧЕТЫРЕХКОЛЕСНОГО КАРТА, ДВИЖУЩЕГОСЯ ПРЯМОЛИНЕЙНО НА СКОРОСТИ С ПРЕПЯТСТВИЕМ

 

Подобный случай описан в п. 1.5. Время удара здесь также невозможно определить из-за недостаточности данных, поэтому оно принимается t₁ =0,1 с. Для этих условий, согласно (1.18):

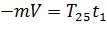, (2.16)

где V – скорость поступательного движения карта до удара (в нашем случае она принимает значение средней V_ср и максимальной скоростей V_max, м/с); 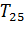– сила, действующая на собак через упряжь со стороны резко и внезапно остановленного карта, Н. Знак «– «показывает, что импульс силы направлен противоположно направлению скорости поступательного движения карта до удара.

Таким образом,

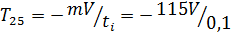. (2.17)

Подставляя в формулу (2.17) значения средней и максимальной скоростей, получим силу, действующую на собак в процессе столкновения с препятствием, которую занесем в таблицу 2.5.

Таблица 2.5

V, м/с	9,17	13,89
Т25, Н	10545,5	15973,5

 

 

3. НАРТЫ

 

Нарты представляют собой санную повозку, размещенную на полозьях (рис. 14, 15) для движения по снегу. Полозья (лыжи) изготовлены из углепластика неизвестного состава. Нарты снабжены двумя системами торможения: плавной (постепенной), путем вдавливания в снежный покров резино-полимерной пластины с протектором (рис. 16), и экстренной (резкой) – путем вдавливания в снег сдвоенного стального тормозного штифта-ножа, увенчанного по верху горизонтальной пластиной, дающей бульдозерный эффект (рис. 17).

 

Рис. 14. Нарты

 

Рис. 15. Нарты (вид сбоку)

Рис. 16. Плавный тормоз нарт

 

Рис. 16. Экстренный тормоз нарт в действии

 

Собственная масса нарт может достигать 45 кг, но в исследуемом случае m _н = 15 кг. Максимальная скорость движения V_max = 50 км/ч =13,89 м/с. Средняя скорость движения V_ср = 33 км/ч = 9,17 м/с. Средняя масса наездника принимается m_ч = 80 кг. Общий вес G нарт с наездником составляет:

G = (m_н+m_ч)g, (3.1)

где g = 9,81 м/с² – ускорение свободного падения.

G = (15 + 80)*9,81 = 931,95 Н.

 

3.1. РАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ НАРТ В УПРЯЖКЕ

 

При равномерном движении по прямой, на нарты действуют следующие силы, изображенные на рис. 17: G – вес нарт с наездником; R_д – сила сопротивления передвижению нарт, равная силе трения скольжения; Т₃₁ – толкающая сила, воздействующая на нарты через потяг от упряжи собак.

 

Рис. 17. Силы, действующие на нарты при прямолинейном равномерном движении

 

Уравнение движения имеет вид:

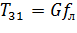, (3.2)

где f_л – коэффициент трения скольжения при движению лыж по снегу. В разных литературных источниках этот коэффициент принимается различным, сильно зависящим от состояния снега и состава материала лыж. Минимальное найденное значение f_л = 0,02 [5] – для температуры воздуха около -20^оС, включением в состав углепластика полиэтилена и графита. Максимальное найденное значение f_л = 0,2 [6] для условий движения углепластиковых лыж с добавлением фторопласта по липкому, загрязненному грунтом, снегу.

С учетом найденного значения G получим формулу для данного случая:

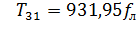. (3.3)

Подставляя f _л получим результаты вычислений и сведем их в таблицу 3.1.

Таблица 3.1

fл	0,02	0,2
T31, Н	18,64	186,39

 

 

3.2. РАВНОЗАМЕДЛЕННОЕ ДВИЖЕНИЕ НАРТ НА ПОДЪЕМЕ В ГОРУ

 

Будем считать, что угол подъема не превышает α = 25^о [опыт заездов]. Схема сил, действующих на нарты, изображена на рис. 18.

 

 

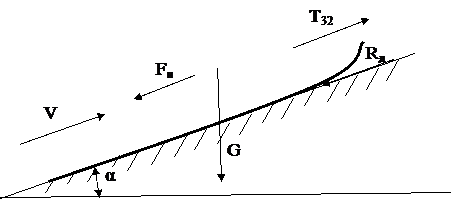Рис. 18. Схема сил, действующих на нарты при равнозамедленном движении в гору

 

Поскольку в санной повозке нет вращающихся масс, то сила инерции 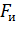обусловлена лишь полной массой нарт с экипажем (m_н + m_ч) и замедлением а, определить которое невозможно из-за недостаточности данных о конкретных условиях. Примем, как и в п. 1.2, 2.2 а ≈ 1 м/с²_. Тогда общее уравнение будет иметь вид:

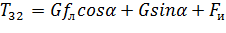, (3.4)

подставляя известные значения получим:

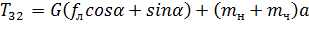, (3.5)

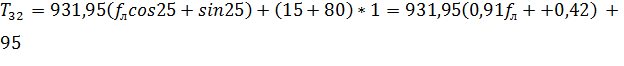. (3.6)

Подставляя в (3.6) f_л, получим значения Т₃₂, которые занесем в таблицу 3.2.

Таблица 3.2

fл	0,02	0,2
T32, Н	503,38	656,03

 

 

3.3. ПРЯМОЛИНЕЙНОЕ РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ НАРТ

 

В отличие от случая, описанного в п. 3.1, на нарты при прямолинейном движении с ускорением, действует сила инерции 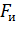, обусловленная полной массой нарт (п. 3.2) и ускорением, принимаемым а = 1 м/с² (рис. 19).

 

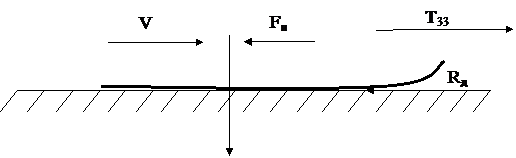Рис. 19. Схема сил, действующих на нарты при прямолинейном равноускоренном движении

 

Уравнение движения нарт имеет вид:

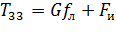, (3.7)

подставляя в (3.7) известные значения получим:

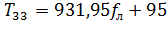. (3.8)

Подставляя в (3.8) коэффициент трения скольжения, получаем значения 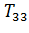, которые заносим в таблицу 3.3.

Таблица 3.3

fл	0,02	0,2
T33, Н	113,64	281,39

 

 

3.4. ДВИЖЕНИЕ НАРТ НА СПУСКЕ ПРИ ТОРМОЖЕНИИ

 

При движении на спуске, гонщик начинает притормаживать и тормозить как плавным, так и экстренным тормозами. Рассмотрим случай макcимальной нагруженности упряжи, когда гонщик тормозит экстренным тормозом, от чего возникает тормозная сила F_т, направленная противоположно скорости движения. Кроме того, сила инерции 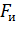, обусловленная полной массой экипажа, направлена не противоположно, а в одну сторону с вектором скорости движения (рис. 20).

 

 

 

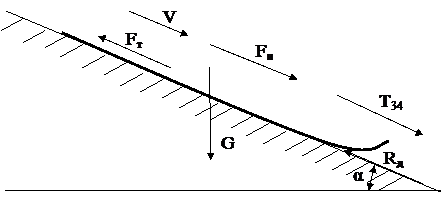Рис. 20. Силы, действующие на нарты при спуске с горы и торможении

 

Уравнение движения нарт выглядит следующим образом:

. (3.9)

Наиболее сложным в определении элементом вышеприведенного уравнения является тормозная сила. Ее нельзя найти, пользуясь стандартными и широко распространенными методиками по расчету тормозов, так как конструкция тормозов нарт не похожа ни на один, описанный в литературе по машинам и механизмам, тормоз. Подобные виды тормозов были применены на аэросанях времен Великой отечественной войны [7], однако методов их расчета найдено не было. Анализируя данное торможение, как сопротивление движению тормозному элементу, входящему под усилием ноги человека в снег, можно отметить, что процесс очень схож с резанием снега, где в качестве ножа применяется зуб весьма сложной формы [8] (рис. 21).

 

 

Рис. 21. Схема резания снега (торможения)

 

Можно определить угол заострения (заточки) β и угол резания ϒ – в нашем случае он близок к 80⁰. С позиции необходимости снижения энергоемкости процессов такой угол резания нельзя назвать рациональным, но если ставить задачу получения максимальной силы сопротивления, то можно с уверенностью отметить, что этот угол выбран верно. Ведь наибольшее сопротивление движению могут испытывать нарты при угле резания снега ϒ около 90⁰. Но при этом значительно возрастает выталкивающая сила, и наезднику придется очень сильно вдавливать в снег тормоз. При незначительном снижении угла резания от 90⁰, выталкивающая сила значительно снижается, и даже наоборот, может стать отрицательной! Снег, как и любой другой грунт, стремится затянуть в свои недра нож тормоза, от чего усилие, прикладываемое человеком значительно меньше. Рассматривая торможение, как резание снега, необходимо сделать незначительное упрощение. Ведь на нож, который режет и снег и любой другой материал, действует сила резания Р, которую принято представлять ее ортогональными составляющими: нормальной P_n, и тангенциальной P_{τ .}. Нормальная составляющая всегда направлена по нормали к плоскости движения ножа, от плоскости движения к основанию ножа. Именно эта составляющая является выталкивающей. Тангенциальная составляющая всегда направлена в сторону, противоположную направлению движения и резания. Соотношение этих составляющих зависит от угла резания. Будем считать, что все усилие резания ограничивается тангенциальной составляющей силы резания. В общем случае, для нашей задачи, нормальная составляющая усилия резания имеет значение лишь для силы, с которой человек вдавливает в снег нож тормоза. Итак, будем считать, что Р = Р_τ.

На силу сопротивления резания влияют прочностные факторы материала резания (снега), углы заострения и резания, скорость резания, ширина ножа, глубина резания, форма режущего ножа. Попытка учесть многие из этих факторов предпринята в работе [9, стр. 28]. Однако это исследование справедливо лишь для одиночных ножей, хотя и уплотненного снега. Нож, который применяется в исследуемой схеме нарт, никак нельзя отнести к одиночным (рис. 22).

 

 

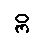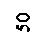
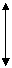
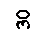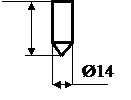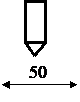Рис. 22. Схема ножевого тормоза нарт