Числовой метод (Разенброка).

Одномерная оптимизация и многомерная безусловная оптимизация.

Контрольная работа по дисциплине

"Оптимальное управление"

ЯГТУ 27.03.04-003 к/р №1

 

Контрольную работу выполнил

студент гр. ……………………..

________________......................

 

…….

Одномерная оптимизация.

Функция имеет вид:

1) Аналитическое решения:

Ответ: точка мнима функции.

2) Решения численным методом (метод параболической аппроксимации).

где: d_ij=x_i²-x_j² _ij=-2,9,20.

Из системы вычислим коэффициенты С₂, С₁, С_0.

Из выражения

Так как точка x*=2 лежит между x₁ и х₂ выбираем новые значения х₁⁽¹⁾=а=-2; х₂⁽¹⁾= х₃⁽¹⁾= х₂⁽⁰⁾=9

Из выражения

Ответ: значения 2 является минимумом функции.

 

 

Решения задачи в среде МATLAB.

>> x=-2:0.05:20;

y=(x-2).^2;

plot(x,y);grid on;title('График');xlabel('ось f(x)');xlabel('ось x')

options=optimset('Display','iter');

>> [x,fval,exitflag,output]=fminbnd('myfun',0,05,options);

f =

0.0081306

Func-count x f(x) Procedure

1 1.90983 0.00813062 initial

f =

1.1885

2 3.09017 1.18847 golden

f =

0.67184

3 1.18034 0.671843 golden

f =

4 2 0 parabolic

f =

1.1131e-009

5 2.00003 1.1131e-009 parabolic

f =

1.1131e-009

6 1.99997 1.1131e-009 parabolic

Optimization terminated:

the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-004

Многомерная безусловная оптимизация

Аналитическое решения функции.

Матрица Гессе отрицательная и А=2>0 значение (f) тоже отрицательная из этого следует функция вогнутая и точка(0,3) является глобальным минимумом.

Графический анализ функции.

Для построения линии уровня функции:

Выбираем следующие значения функции: 10, 25, 50.

Выражаем переменную через и функцию .

 

Точка минимума имеет координатыпо

F	X1	-X2	+X2
	-4	2,35	7,65
-2
	1,36	7,36
	-2
	-1,65	3,65
	-1
	-4	0,31	9,69
-2	-1,57	9,57
	-2,83	8,83
	-3,57	7,57
	-3,69	5,69
	-3,4	4,4
	-4	-1,86	11,86
-2	-3,48	11,48
	-4,68	10,68
	-5,48	9,48
	-5,85	7,85

Числовой метод (Разенброка).

Найдем минимум функции

1. Зададим начальные точку

Положим

2⁰. Так как

3⁰. Так как и перейдем к шагу 2.

 

2¹. Так как

3¹. Так как 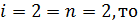проверим успешность поиска по текущему ортогональному направлению поиск успешный. Положим и перейдем к шагу 2.

 

2². Так как

3². Так как и перейдем к шагу 2.

2³. Так как

3³. Так как 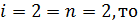проверим успешность поиска по текущему ортогональному направлению поиск успешный. Положим и перейдем к шагу 2.

2⁴. Так как

3⁴. Так как и перейдем к шагу 2.

2⁵. Так как

3⁵. Так как 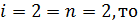проверим успешность поиска по текущему ортогональному направлению поиск успешный. Положим и перейдем к шагу 2.

2⁶. Так как

3⁶. Так как и перейдем к шагу 2.

2⁷. Так как

3⁷. Так как , но перейдем к шагу 4.

4⁰. Положим ,Так как из соотношения.

Построрем новый нобор напровленийпоеска;

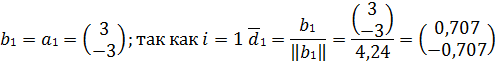
Положим

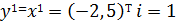и перейдем к шагу 2.

2⁸. Так как

3⁸. Так как и перейдем к шагу 2.

2⁹. Так как

3⁹. Имеем , положим перейдем к шагу 2.

2¹⁰. Так как

3¹⁰. Так как и перейдем к шагу 2.

2¹¹. Так как

3¹¹. Имеем , то перейдем к шагу 4.

4¹. Положим ,Так как из соотношения.

Построрем новый нобор напровленийпоеска;

Положим

и перейдем к шагу 2.

2¹². Так как

3¹². Так как и перейдем к шагу 2.

2¹³. Так как

3¹³. Имеем , выполнили одну не удачную серию шагов на последней серии справедлива неравенства . Поэтому положим и перейдем к шагу 2.

2¹⁴. Так как

3¹⁴. Так как и перейдем к шагу 2.

2¹⁵. Так как

3¹⁵. Имеем , выполнили вторую не удачную серию шагов на последней серии справедлива неравенства . Поэтому положим и перейдем к шагу 2.

2¹⁶. Так как

3¹⁶. Так как и перейдем к шагу 2.

2¹⁷. Так как

3¹⁷. Имеем , выполнили вторую не удачную серию шагов на последней серии справедлива неравенства . Поэтому положим и перейдем к шагу 2.

2¹⁸. Так как

3¹⁸. Так как и перейдем к шагу 2.

2¹⁹. Так как

3¹⁹. Имеем , положим перейдем к шагу 2.

2²⁰. Так как

3²⁰. Так как и перейдем к шагу 2.

2²¹. Так как

3²¹. Имеем , то перейдем к шагу 4.

4². Положим ,Так как из соотношения.

Построрем новый нобор напровленийпоеска;

Положим

и перейдем к шагу 2.

2²². Так как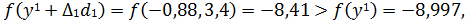

3²². Так как и перейдем к шагу 2.

2²³. Так как

3²³. Имеем , выполнили одну не удачную серию шагов на последней серии справедлива неравенства . Поэтому положим и перейдем к шагу 2.

2²⁴. Так как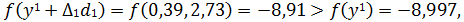

3²⁴. Так как и перейдем к шагу 2.

2²⁵. Так как

3²⁵. Имеем , выполнили вторую не удачную серию шагов на последней серии справедлива неравенства . Поэтому положим и перейдем к шагу 2.

2²⁶. Так как

3²⁶. Так как и перейдем к шагу 2.

2²⁷. Так как

3²⁷. Имеем , выполнили третий не удачную серию шагов на последней серии справедлива неравенства . Поэтому положим и перейдем к шагу 2.

2²⁸. Так как

3²⁸. Так как и перейдем к шагу 2.

2²⁹. Так как

3²⁹. Имеем , выполнили четвертый не удачную серию шагов на последней серии справедлива неравенства . Поэтому положим и перейдем к шагу 2

2³⁰. Так как

3³⁰. Так как и перейдем к шагу 2.

2³¹. Так как

3³¹. Имеем , выполнили пятый не удачную серию шагов на последней серии справедлива неравенства . Поэтому положим и перейдем к шагу 2

2³². Так как

3³². Так как и перейдем к шагу 2.

2³³. Так как

3³³. Имеем 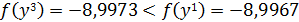, положим 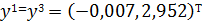перейдем к шагу 2.

2³⁴. Так как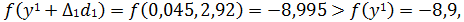

3³⁴. Так как и перейдем к шагу 2.

2³⁵. Так как

3³⁵. Имеем , то перейдем к шагу 4.

4³. Положим ,Так как .

Ответ: x*=(-0,007, 2,952) точка минимума она приближается к точке x*=(0, 3)=-9 которая является минимумом.

>> [x1,x2]=meshgrid(-20:0.12:100,-20:0.12:100);

y=x1.^2+x2.^2+x1.*x2-3.*x1-6.*x2;

mesh(x1,x2,y);

x0=[-5 8];

myfun(x0);

[x,fval,exitflag,output]=fminbnd('myfun',0,12,options);

Attempted to access x(2); index out of bounds because numel(x)=1.

 

Error in myfun (line 4)

f=x(1).^2+x(2).^2+x(1).*x(2)-3.*x(1)-6.*x(2);

 

Error in fminbnd (line 217)

x= xf; fx = funfcn(x,varargin{:});