Биометрическая обработка данных
Цель работы: освоить методику биометрической обработки данных.
Ход работы:
1. Изучить формулы, применяемые для расчета основных биометрических параметров: средней арифметической величины, дисперсии, среднего квадратического отклонения, коэффициента вариации, ошибки средней арифметической, и оценки статистической значимости найденных параметров.
2. Произвести биометрическую обработку данных, полученных в ходе проведения биологического мониторинга окружающей среды и эколого-эпидемиологических работ.
Общие замечания:
Конечной целью исследования является нахождение параметров (показателей), xapaктеризующих свойства генеральной совокупности. Генеральная совокупность - это вce объекты изучаемой категории. Выборочная совокупность (выборка) - это часть генеральной совокупности, выделенная по специальным правилам и предназначенная для ее характеристики.
вторая практика
Основные биометрические параметры
1.1. Вариант, или дата (от лат. variantis - изменяющийся; видоизменение, разновидность) - это результат измерения признака у отдельного объекта исследования. Обозначается буквами V или х.
1.2. Объем выборки. Численность совокупности характеризуется числом наблюдений - N (числом измеренных объектов, вариантов или дат). Различают малую (N≤.20..30) и большую (N≥20...30) совокупности.
Результаты наблюдений в большой выборке можно представить в виде вариационного ряда. Класс - это часть совокупности, в которой объединены все сходные по величине изучаемого признака объекты (варианты). Числовые значения класса (его границы) обозначаются буквой W. Количество вариантов в каждом отдельном классе называется частотой и обозначается буквой n. Объем выборки равен сумме частот вариантов во всех классах ряда (N =Σn).
Вариационный ряд - это двойной ряд чисел, из которых один указывает значения признака в классах W, a другой - число объектов в классах n. Классы располагают в порядке возрастания или убывания значения признака W, причем интервал между ними для всего вариационного ряда один и тот же. В нашем примере это 5: каждый клacc oт соседнего W отличается на 5:
Вариации или
классы, W 1-5 6-10 11-15 16-20 21-25 26-30
Частоты, n 2 4 7 5 4 3
N =Σn = 2+4+ 7 + 5+4 + 3 = 25.
1.3. Средняя арифметическая величина определяется путем деления суммы всех значений признаков (суммы дат) на объем совокупности:
M=  ,
,
где V - вариант, или дата (значение признака у отдельного объекта;
∑ (сигма большая) - знак суммирования; N – объем совокупности (число наблюдений).
1.4. Лимиты (lim), или пределы lim = Vmin…Vmax. Границы разнообразия определяются крайними вариантами, т.е. максимальным и минимальным значением признака в совокупности.
1.5. Размах разнообразия - ρ=Vmax-Vmin. Чем меньше ρ, тем меньше разнообразие и наоборот.
1.6. Дисперсия С, или сумма квадратов центральных отклонений, т.е. сумма квадратов разности между значением каждого отдельного варианта V и средней арифметической величиной М:
С = Σ(V - М)2
1.7. Варианса σ2 - сигма в квадрате, или средний квадрат центральных отклонений, вычисляется по формуле:
σ2 =  .
.
Выражение N-1 называют числом степеней свободы и обозначают υ. Сумму квадратов центральных отклонений делят не на объем совокупности N, а на число объектов, не соответствующих средней арифметической (N-1), так как считается, что один из объектов представлен средней арифметической величиной.
1.8. Среднее квадратическое отклонение от средней арифметической величины - основной показатель разнообразия значений признака в группе. Используется для определения целого ряда других параметров совокупности (коэффициента вариации, ошибки средней арифметической величины и др.):
σ =  .
.
σ берется как положительное значение квадратного корня, является величиной именованной (выражается в единицах измерения признака) и показывает, насколько в среднем каждый вариант отличается от средней арифметической величины.
1.9. Коэффициент вариации показывает, какую часть σ составляет oт средней арифметической величины.
Cv= σ / М х 100.
Выражается в долях единиц или процентах, т.е. является относительной величиной, что позволяет использовать его для сравнения степени разнообразия различных признаков и разных групп (выраженных в разных единицах измерения). Р азнообразие входящих в совокупность объектов обычно обусловлено изменчивостью.
1.10. Нормированное отклонение, т.е. абсолютное отклонение каждого варианта от средней арифметической величины, выраженное в долях сигмы. Нормированное отклонение определяется по формуле:
t= 
 .
.
Заменив фактические значения признака на нормированное отклонение и отложив t на оси абсцисс, получим числовой ряд с нулевым значение в центре, с отрицательными слева и с положительными справа от 0.
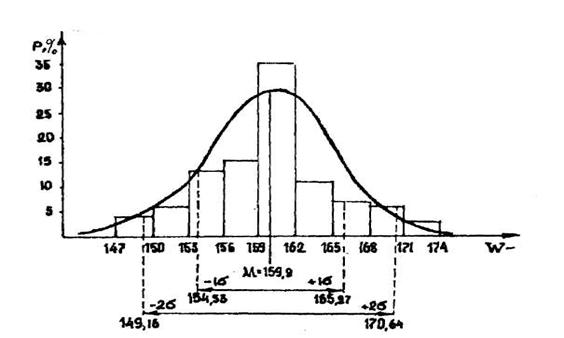
|
Чем больше сигма, тем шире кривая, а ее максимальная высотаниже, и наоборот. При проведении исследования важно найти долю всех вариантов, отклоняющихся от средней на определенную величину, т.е. установить, какая часть вариантов находится в пределах от M – tσ до M + tσ (или M ± tσ). Существуют специальные таблицы, в которых приведены доли вариантов, лежащих в указанных пределах с шагом измерения в t, равным 0,1 или даже 0,01. Так, в пределах от M – 1σ до M + 1σ лежит 0,6828 (68,3 %) всех вариантов в нормально распределенной совокупности; от M – 2σ до M + 2σ – 0,9545 (95,5 %) всех вариантов; от M – 3σ до M + 3σ – 0,9973 (99,73 %). Указанные процентные значения фактически характеризуют вероятность В нахождения вариантов в заданных пределах.
В биологических исследованиях используются три основных уровня вероятности (уровня надежности выводов) и соответствующие им значения t, называемые критериями надежности выводов. Вероятности В=0,95 соответствует значение критерия t=1,96 (округленно t = 2). Такой уровень вероятности означает, что 95 случаев наблюдений из 100 находится в границах от М-1,96σ до М+1,96σ. Второй уровень надежности - повышенный В=0,99, ему соответствует значение t=2,57 (округленно 2,6), т.е. 99 случаев наблюдений из 100 находится в границах от М-2,57σ до М+2,57σ; вероятности В=0,999 соответствует t=3,29 (округленно 3,3). Эти вероятности получили название доверительных, а указанные границы: M ± 2σ, M ± 2,6σ и M ± 3,3σ и интервалы между ними называют доверительными границами и доверительными интервалами для соответствующих доверительных вероятностей.
Иногда пользуются не значениями доверительных вероятностей В (т.е. вероятностями того, что параметр будет находиться в заданных доверительных границах), а соответствующими им уровнями значимости р: р<0,05, р<0,01 и р<0,001. Эти уровни показывают вероятность нахождения параметра за пределами доверительных границ, т.е. определяют вероятность ошибки.
Английским статистиком Госсетом, публиковавшим свои работы под псевдонимом Стьюдент, составлены теоретически обоснованные таблицы (таблицы стандартных значений критерия Стьюдента), где для доверительных вероятностей (В1=0,95; В2=0,99; В3=0,999) указаны значения t в зависимости от числа объектов. Следует обратить внимание на то, что объем выборки N становится больше по мере увеличения надежности выводов (возрастает t), т.е. по мере повышения точности планируемого исследования.

- Источник статистических ошибок. Ошибка средней арифметической
Конечная цель исследований – найти параметры генеральной совокупности. Отличия выборочных параметров от генеральных имеют объективную природу, т.е. возникают независимо от исследователя всегда, когда по части (выборке) пытаются охарактеризовать целое (генеральную совокупность). Источниками статистических ошибок являются ограниченность объема выборки и случайность отбора объектов. Не следует путать их с ошибками другого рода: типичности (когда выборка составлена неправильно и вследствие этого не является репрезентативной), прибора или инструмента при измерении и т.д. Такого рода ошибки не вскрываются биометрическими методами, они должны быть устранены заранее. Отсутствие таких ошибок в результатах измерений дает основание для дальнейшей биометрической обработки материала с целью выявления статистических ошибок (ошибок репрезентативности), которых нельзя избежать при использовании выборочного метода и которые необходимо учитывать, чтобы научно обосновать выводы.
Ошибки репрезентативности показывают степень соответствия выборочных параметров параметрам генеральной совокупности. Чем меньше цифровые значения ошибок, тем точнее вычисленный параметр, тем ближе его значение к значению соответствующего параметра генеральной совокупности.
Ошибки вычисляются для всех выборочных параметров и обычно обозначаются буквой m с подстрочным указанием знака того параметра, для которого они определяются: mM, mσ и т.д. Чем большее число объектов отобрано в выборку, тем меньше отклонение выборочных средних от генеральной средней. Таким образом, размер ошибки средней арифметической связан с количеством объектов в выборке. Эта связь выражается формулой:
mM =  .
.
Ошибка выражается в тех же единицах измерения (см, кг, % и т.д.), что и средняя арифметическая и обычно записывается следующим образом: M± mM.
Существует общее правило определения статистической значимости выборочных параметров: отношение выборочного параметра к его ошибке сравнивают с tтабл из таблицы Стьюдента для соответствующего числа степеней свободы (υ=N-1). Если Р/mР≥ tтабл, то выборочный параметр статистически значим и можно указать доверительные границы генерального параметра. Если Р/mР<tтабл, то выборочный параметр статистически незначим, что не позволяет судить о значении параметра в генеральной совокупности.