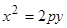Тема: Аналитическая геометрия
Лекция № 7 “Прямая на плоскости. Основные задачи”
1. Общее уравнение прямой.
Пусть на плоскости дана декартова система координат. Движение точки с произвольными координатами 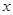 и
и 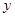 по этой плоскости порождает линию.
по этой плоскости порождает линию.
О1. Любое соотношение 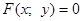 (имеющее смысл в области вещественных чисел), где
(имеющее смысл в области вещественных чисел), где 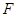 некоторое выражение, связывающее переменные величины
некоторое выражение, связывающее переменные величины 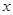 и
и 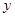 , называется уравнением с двумя неизвестными, которое определяет линию. Точки, принадлежащие линии, удовлетворяют приведенному соотношению, а точки вне линии – не удовлетворяют.
, называется уравнением с двумя неизвестными, которое определяет линию. Точки, принадлежащие линии, удовлетворяют приведенному соотношению, а точки вне линии – не удовлетворяют.
О2. Порядок линии определяется по высшему показателю степени переменных 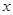 и
и 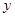 или по сумме показателей степени в произведении этих величин.
или по сумме показателей степени в произведении этих величин.
Пример 1. а) 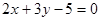 – линия первого порядка; точка
– линия первого порядка; точка  удовлетворяет этому соотношению, а точка, например,
удовлетворяет этому соотношению, а точка, например, 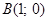 – ему не удовлетворяет;
– ему не удовлетворяет;
б) 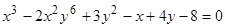 – линия восьмого порядка;
– линия восьмого порядка;
в)  и
и  – линии второго порядка.
– линии второго порядка.
Рассмотрим другое определение линии:
О2. Геометрическое место точек, координаты которых удовлетворяют уравнению 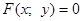 , называется линией, а само уравнение
, называется линией, а само уравнение 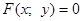 – уравнением линии.
– уравнением линии.
О3. Общим уравнением прямой называется уравнение первого порядка вида 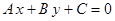 .
.
Рассмотрим частные случаи этого уравнения:
а)  – прямая проходит начало системы координат ( Рис. 20 )
– прямая проходит начало системы координат ( Рис. 20 )

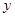
Рис. 20. Прямая, проходящая
через начало координат.
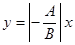

б) 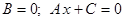 – прямая проходит параллельно оси ординат
– прямая проходит параллельно оси ординат  ( Рис. 21 )
( Рис. 21 )

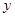
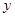
Рис. 21. Прямая, проходящая параллельно
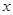
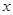 оси ординат
оси ординат  .
.
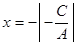
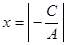
в) 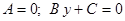 – прямая проходит параллельно оси абсцисс
– прямая проходит параллельно оси абсцисс  ( Рис. 22 )
( Рис. 22 )
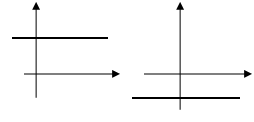
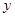
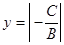 Рис. 22. Прямая, проходящая
Рис. 22. Прямая, проходящая
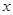
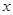 параллельно оси абсцисс
параллельно оси абсцисс  .
.
2. Виды уравнений прямой.
1. Уравнение прямой с угловым коэффициентом. Пусть дано общее уравнение прямой 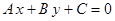 , в котором коэффициент
, в котором коэффициент  . Разрешим общее уравнение прямой относительно переменной
. Разрешим общее уравнение прямой относительно переменной 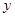 :
: 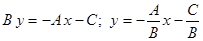 . Обозначим через
. Обозначим через 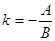 и
и  , тогда уравнение примет вид
, тогда уравнение примет вид 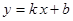 , которое называется уравнением прямой с угловым коэффициентом. Выясним геометрический смысл параметров
, которое называется уравнением прямой с угловым коэффициентом. Выясним геометрический смысл параметров  и
и 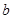 . При
. При 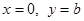 , т.е. параметр
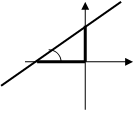
, т.е. параметр 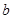 показывает, какой величины отрезок отсекает прямая на оси ординат, считая от начала отсчета. При
показывает, какой величины отрезок отсекает прямая на оси ординат, считая от начала отсчета. При  , т.е. прямая отсекает на оси абсцисс отрезок
, т.е. прямая отсекает на оси абсцисс отрезок  ( Рис. 23 ).
( Рис. 23 ).
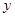
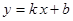 ,
, 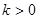
Рис. 23. Отрезки, отсекаемые прямой на
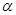
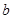 координатных осях.
координатных осях.

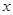
Из рисунка видно, что 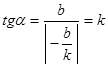 , т.е. угловой коэффициент
, т.е. угловой коэффициент  определяет тангенс угла наклона прямой к положительному направлению оси абсцисс
определяет тангенс угла наклона прямой к положительному направлению оси абсцисс  .
.
2. Уравнение прямой в отрезках.
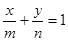 , называется уравнением прямой в отрезках.
, называется уравнением прямой в отрезках.
3. Уравнение прямой, проходящей через две заданные точки.

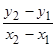 или
или 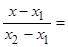
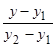 - уравнение называется уравнением прямой, проходящей через две заданные точки
- уравнение называется уравнением прямой, проходящей через две заданные точки 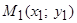 и
и 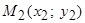 .
.
4. Уравнение прямой, проходящей через заданную точку  параллельно заданному вектору
параллельно заданному вектору 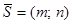 ( каноническое уравнение прямой ). Пусть прямая проходит через заданную точку
( каноническое уравнение прямой ). Пусть прямая проходит через заданную точку  параллельно вектору
параллельно вектору 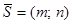 .
.
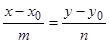 . Полученное уравнение называется либо уравнением, проходящим через заданную точку параллельно направляющему вектору, либо каноническим уравнением прямой.
. Полученное уравнение называется либо уравнением, проходящим через заданную точку параллельно направляющему вектору, либо каноническим уравнением прямой.
5. Параметрическое уравнение прямой. Если каждую дробь в каноническом уравнении прямой приравнять некоторому параметру  , то получим параметрическое уравнение прямой
, то получим параметрическое уравнение прямой  .
.
3. Основные задачи.
1. Координаты точки пересечения двух прямых. Пусть две прямые заданы общими уравнениями  . Требуется найти координаты точки пересечения этих прямых. Для того чтобы вычислить координаты точки пересечения
. Требуется найти координаты точки пересечения этих прямых. Для того чтобы вычислить координаты точки пересечения  , необходимо решить вышеприведенную систему линейных алгебраических уравнений, так как координаты точки
, необходимо решить вышеприведенную систему линейных алгебраических уравнений, так как координаты точки  должны одновременно удовлетворять уравнениям прямых
должны одновременно удовлетворять уравнениям прямых  и
и 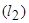 .
.
2. Угол между двумя пересекающимися прямыми. Пусть даны две пересекающиеся прямые, заданные уравнениями с угловыми коэффициентами
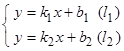 . Требуется найти угол между этими прямыми ( Рис. 26 ).
. Требуется найти угол между этими прямыми ( Рис. 26 ).

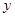

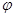
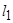
Рис. 26. Угол между двумя прямыми.
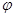

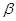
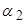
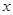
 . Из полученной формулы видно:
. Из полученной формулы видно:
а) если прямые  и
и 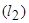 параллельны или совпадают (
параллельны или совпадают (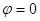 или
или 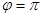 ), то
), то 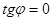 . Отсюда следует условие параллельности прямых: угловые коэффициенты прямых равны между собой
. Отсюда следует условие параллельности прямых: угловые коэффициенты прямых равны между собой 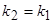 .
.
а) если прямые  и
и 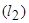 перпендикулярны (
перпендикулярны ( ), то
), то 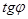 не существует. Отсюда следует условие перпендикулярности прямых: угловые коэффициенты прямых связаны между собой соотношением
не существует. Отсюда следует условие перпендикулярности прямых: угловые коэффициенты прямых связаны между собой соотношением 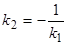 .
.
Пример 4. Определить угол между прямыми 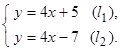
В силу того, что  , то прямые параллельны, следовательно,
, то прямые параллельны, следовательно, 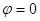 .
.
Пример 5. Выяснить взаимное расположение прямых 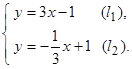
Так как угловые коэффициенты 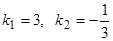 и связаны между собой соотношением
и связаны между собой соотношением 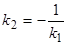 , то прямые взаимно перпендикулярны.
, то прямые взаимно перпендикулярны.
3. Расстояние от точки до прямой. Расстояние от точки до прямой определятся вдоль перпендикуляра, опущенного из точки  на прямую
на прямую  . Если прямая
. Если прямая  задана общим уравнением, то расстояние от точки до прямой
задана общим уравнением, то расстояние от точки до прямой
определяется формулой:  . Если прямая
. Если прямая  задана уравнением прямой с угловым коэффициентом, то расстояние от точки до прямой определяется формулой:
задана уравнением прямой с угловым коэффициентом, то расстояние от точки до прямой определяется формулой:  .
.
Лекция № 8 “Кривые второго порядка”
1. Окружность.
О1. Кривой второго порядка называется линия, описываемая уравнением 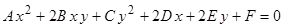 .
.
З1. Если коэффициенты 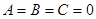 , уравнение кривой II порядка вырождается в уравнение прямой.
, уравнение кривой II порядка вырождается в уравнение прямой.
При определенных значениях параметров, входящих в это уравнение, оно дает канонические уравнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.
О2. Окружностью называется геометрическое место точек равноудаленных от выделенной точки  , называемой центром окружности, на
, называемой центром окружности, на
расстояние  , которое называется радиусом окружности.
, которое называется радиусом окружности.
Получим уравнение окружности ( Рис. 27 ). Пусть точка 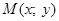 лежит на окружности
лежит на окружности
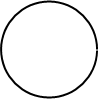

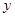
Рис. 28. Окружность.
 |
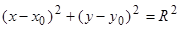

Если 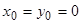 , то уравнение принимает вид
, то уравнение принимает вид  , которое называется каноническим уравнением окружности.
, которое называется каноническим уравнением окружности.
2. Эллипс.
О3. Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек 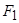 и
и  , называемых фокусами эллипса, есть величина постоянная и равная
, называемых фокусами эллипса, есть величина постоянная и равная  .
.
Расстояние между фокусами (фокусное расстояние) равно  .
.
каноническое уравнение эллипса:  . Если
. Если 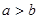 , то эллипс вытянут вдоль оси
, то эллипс вытянут вдоль оси  , при выполнении противоположного неравенства – вдоль оси
, при выполнении противоположного неравенства – вдоль оси  (при этом фокусы тоже расположены на этой оси). Найдем координаты точек пересечения эллипса с координатными осями:
(при этом фокусы тоже расположены на этой оси). Найдем координаты точек пересечения эллипса с координатными осями:
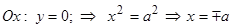 , т.е. точками пересечения эллипса с осью абсцисс будут точки
, т.е. точками пересечения эллипса с осью абсцисс будут точки 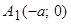 и
и 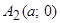 ;
;
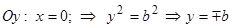 , т.е. точками пересечения эллипса с осью ординат будут точки
, т.е. точками пересечения эллипса с осью ординат будут точки 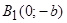 и
и 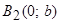 ( Рис. 30 ).
( Рис. 30 ).
О4. Найденные точки называются вершинами эллипса.
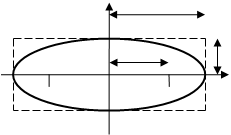
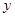

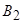
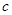
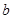 Рис. 30. Вершины, фокусы и параметры
Рис. 30. Вершины, фокусы и параметры
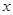 эллипса.
эллипса.

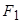
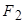
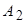
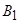
О5. Если 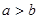 , то параметр
, то параметр  называется большой, а параметр
называется большой, а параметр 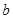 – малой полуосями эллипса.
– малой полуосями эллипса.
О6. Эксцентриситетом эллипса называется отношение фокусного расстояния к большой полуоси эллипса  .
.
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 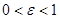 .
.
Пример 1. Составить уравнение эллипса, если его большая полуось  , а его эксцентриситет
, а его эксцентриситет 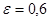 .
.
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр  :
: 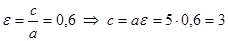 . Зная параметр
. Зная параметр 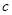 , можно вычислить малую полуось эллипса
, можно вычислить малую полуось эллипса  . Следовательно, каноническое уравнение заданного эллипса имеет вид:
. Следовательно, каноническое уравнение заданного эллипса имеет вид:  .
.
3. Гипербола.
О7. Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек 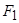 и
и 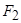 , называемых фокусами гиперболы, есть величина постоянная и равная
, называемых фокусами гиперболы, есть величина постоянная и равная  .
.
Каноническое уравнение гиперболы: 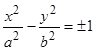 . Для знака “+” фокусы гиперболы расположены на оси
. Для знака “+” фокусы гиперболы расположены на оси 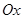 , вдоль которой вытянута гипербола. Для знака “–” фокусы гиперболы расположены на оси
, вдоль которой вытянута гипербола. Для знака “–” фокусы гиперболы расположены на оси  , вдоль которой вытянута гипербола. Найдем координаты точек пересечения гиперболы с координатными осями:
, вдоль которой вытянута гипербола. Найдем координаты точек пересечения гиперболы с координатными осями:
 , т.е. точками пересечения гиперболы с осью абсцисс будут точки
, т.е. точками пересечения гиперболы с осью абсцисс будут точки 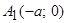 и
и  ;
;
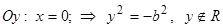 , т.е. гипербола не пересекает ось ординат.
, т.е. гипербола не пересекает ось ординат.
О8. Найденные точки 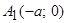 и
и  называются вершинами гиперболы.
называются вершинами гиперболы.
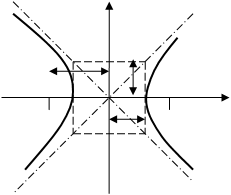
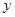
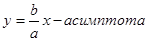
Рис. 32. Асимптоты и параметры гипер-
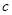
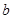 гиперболы.
гиперболы.
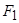
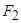
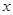

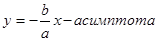
О9. Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы.
В данном конкретном случае параметр  называется действительной, а параметр
называется действительной, а параметр 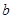 – мнимой полуосями гиперболы.
– мнимой полуосями гиперболы.
О10. Эксцентриситетом гиперболы называется отношение фокусного
расстояния к действительной полуоси гиперболы  .
.
Из определения эксцентриситета гиперболы следует, что он удовлетворяет
неравенству  . Если эксцентриситет
. Если эксцентриситет  , то
, то  и гипербола становится равнобочной. Если
и гипербола становится равнобочной. Если  , то
, то 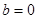 и гипербола вырождается в два полубесконечных отрезка
и гипербола вырождается в два полубесконечных отрезка  и
и  .
.
Пример 2. Составить каноническое уравнение гиперболы, если мнимая полуось 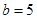 и гипербола проходит через точку
и гипербола проходит через точку 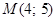 .
.
Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины: 
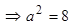 . Следовательно, каноническое уравнение гиперболы имеет вид
. Следовательно, каноническое уравнение гиперболы имеет вид 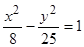
4. Парабола.
О11. Параболой называется геометрическое место точек равноудаленных от выделенной точки  , называемой фокусом параболы, и прямой
, называемой фокусом параболы, и прямой 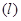 , называемой директрисой.
, называемой директрисой.
Каноническое уравнение параболы: 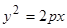 (а также аналогичные ему, см. Рис. 34). Найдем координаты точек пересечения параболы с координатными осями:
(а также аналогичные ему, см. Рис. 34). Найдем координаты точек пересечения параболы с координатными осями:
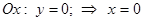 , т.е.
, т.е. 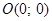 – точка пересечения параболы с осью абсцисс;
– точка пересечения параболы с осью абсцисс;
 , т.е.
, т.е. 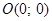 – точка пересечения параболы с осью ординат.
– точка пересечения параболы с осью ординат.
О12. Точка 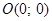 называется вершиной параболы.
называется вершиной параболы.
Пример 3. Дано уравнение параболы 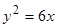 . Определить координаты фокуса параболы и составить уравнение параболы.
. Определить координаты фокуса параболы и составить уравнение параболы.
Так как из уравнения параболы 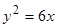 следует, что
следует, что 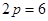 , следовательно
, следовательно 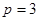 . Таким образом, фокус этой параболы лежит в точке
. Таким образом, фокус этой параболы лежит в точке  , а уравнение параболы имеет вид
, а уравнение параболы имеет вид  .
.

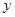
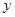
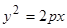
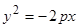
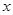
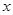 Рис. 34. Параболы и их
Рис. 34. Параболы и их
уравнения.