Прежде чем определить геометрические характеристики, проверим, к какому типу относится панель. Для этого проверим условия:
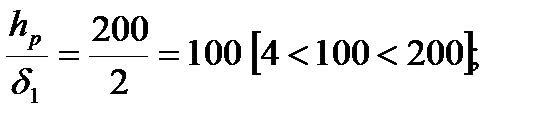
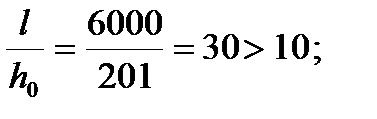
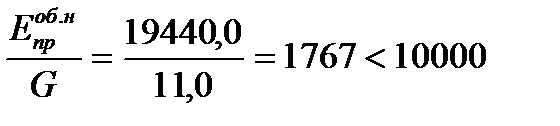 ,
,
где 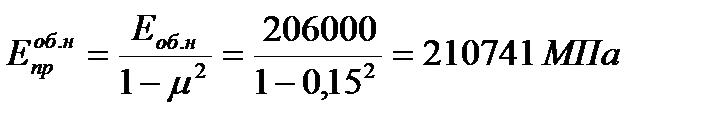 .
.
Условия выполняются, следовательно, панель относится к четвертому типу (согласно классификации [1]), то есть к панелям со сплошным срединным слоем. Для таких панелей обрамляющие ребра, расположенные по контуру, в работе не учитываются. Геометрические характеристики подсчитывают без учета срединного слоя для расчетной полосы, равного 1 м. Принимая во внимание, что обшивки сделаны из различного материала, то все геометрические характеристики будем приводить к материалу верхней обшивки.
Приведенный статический момент
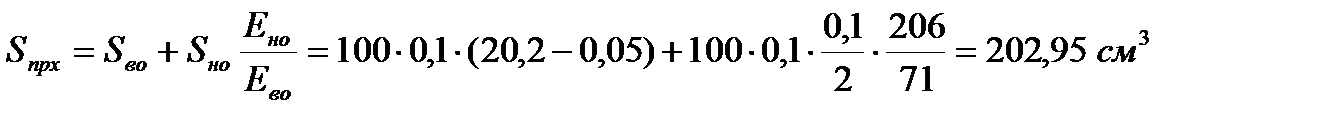 .
.
Площадь, приведенная к материалу верхней обшивки
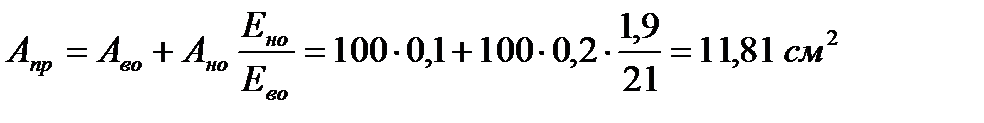 .
.
Определяем положение нейтральной оси
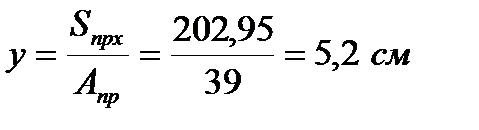 .
.
Приведенный момент инерции относительно нейтральной оси
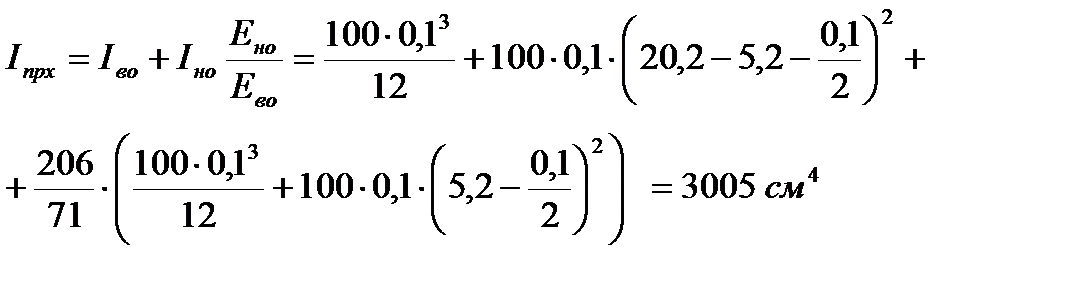
Приведенный момент сопротивления
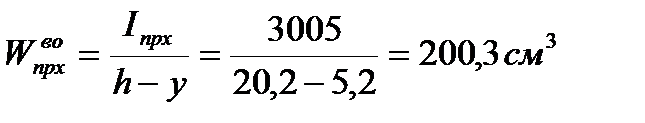 ,
,
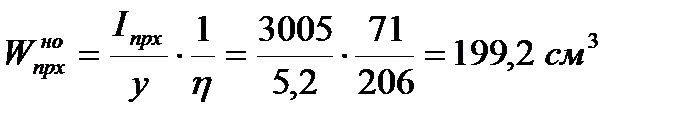 .
.
Определение расчетных усилий
Проверяем, не относится ли панель к гибким пластинам, используя выражения:
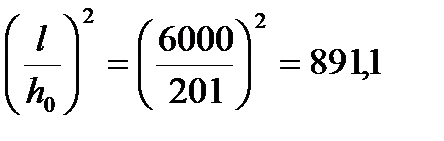 ;
;
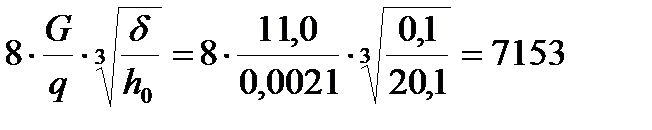
886,65<7153, следовательно, панель не относится к гибким пластинам. Рассчитываем панель, как свободнолежащую балку на двух опорах с расчетным пролетом 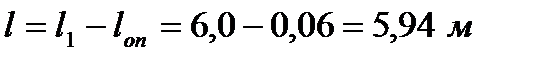 .
.
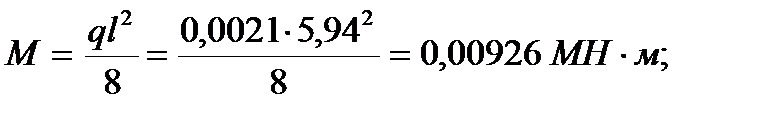
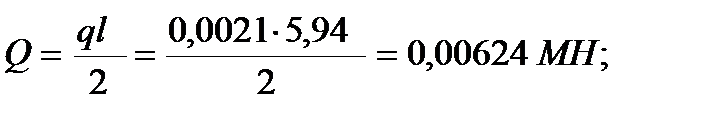
Проверка несущей способности панели
Проверка прочности растянутой обшивки:
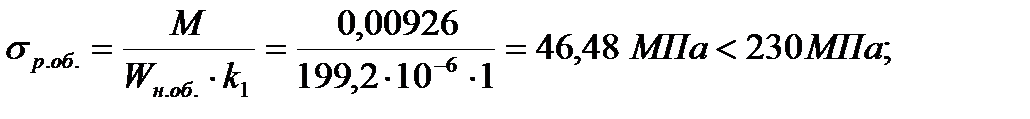
Так как толщина сжатой обшивки меньше 4 мм., то прочность ее проверяем с учетом начальной кривизны по формуле
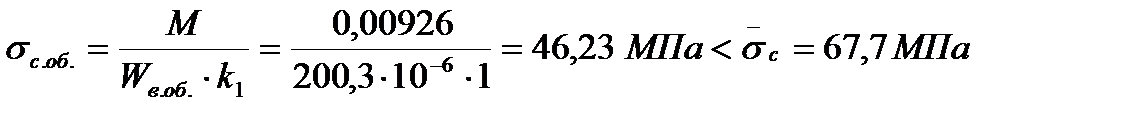 ,
,
где 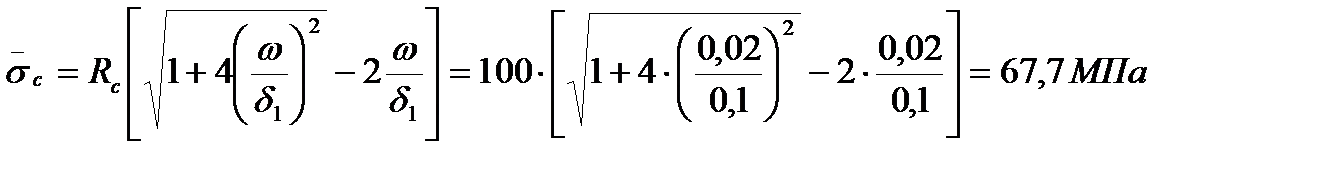 .
.
Проверка прочности срединного слоя
-по нормальным напряжениям
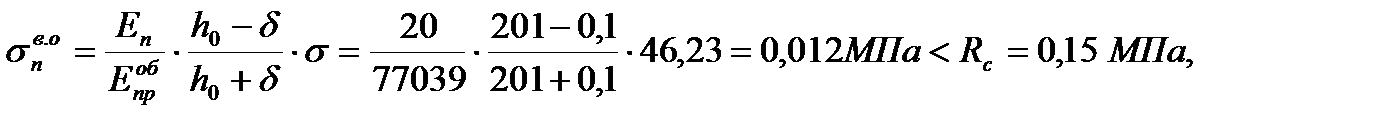
где 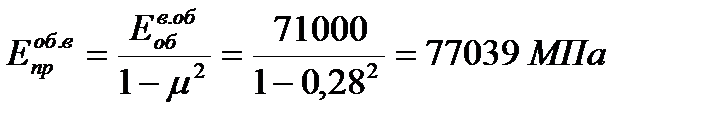 ;
;
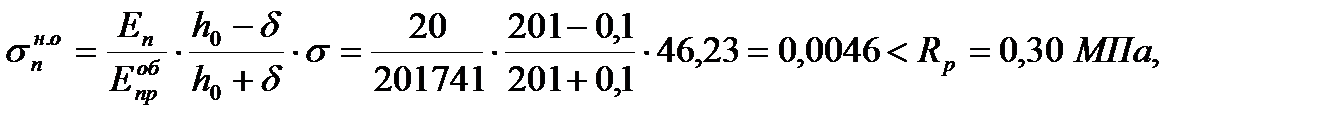
-по касательным напряжениям
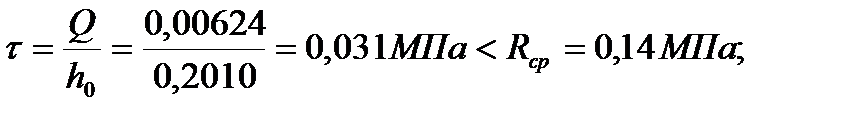
-по эквивалентным напряжениям
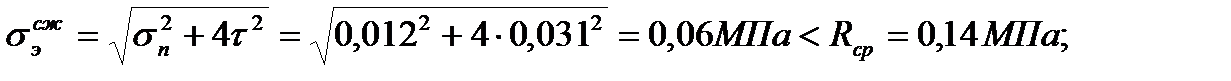
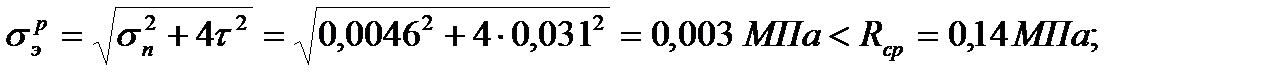
Проверка прогибов панели
Изгибная жесткость панели с учетом податливости срединного слоя равна:
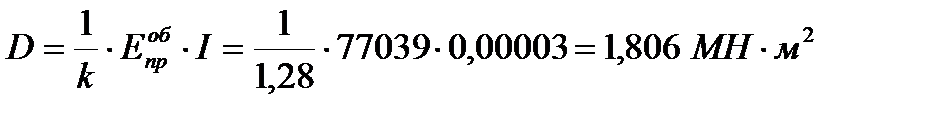 ,
,
где 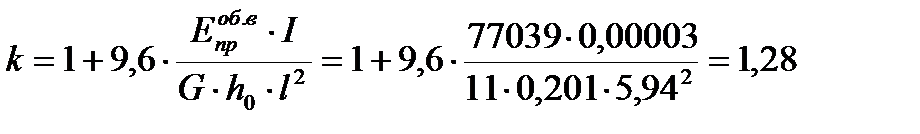 .
.
Проверяем прогиб панели по формуле:
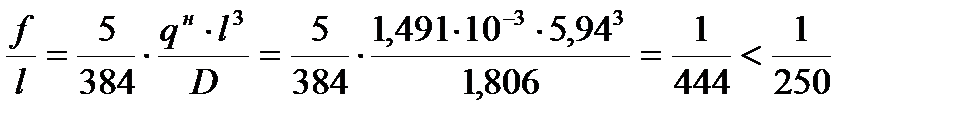 .
.
Расчет на местные нагрузки
|
|
В качестве местной нагрузки принимаем монтажный груз Pн=1000 Н с коэффициентом надежности 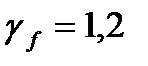 . Интенсивность действия местной нагрузки
. Интенсивность действия местной нагрузки
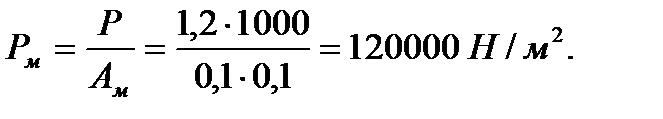
Радиус приведенного круга:
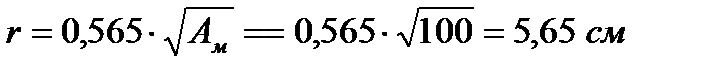 .
.
Значения коэффициентов 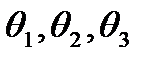 при характеристике
при характеристике
1) 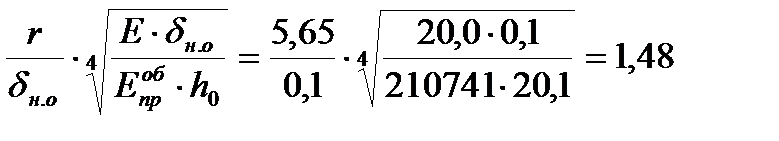 ;
;
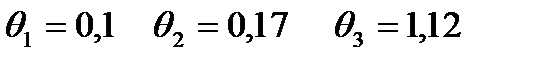 .
.
2) 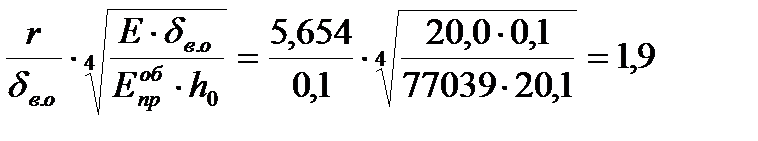 ;
;
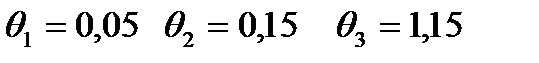 .
.
Проверяем прочность:
а) по нормальным напряжениям в обшивке:
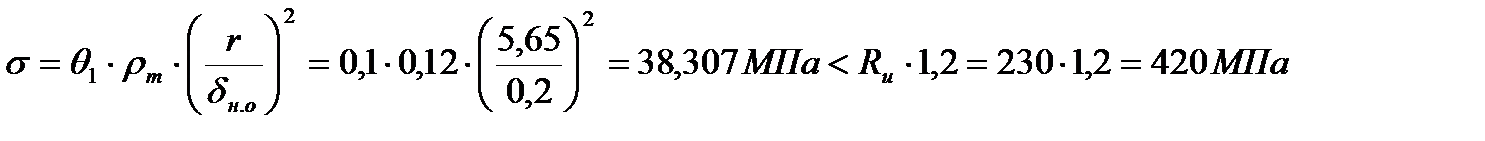 ,
,
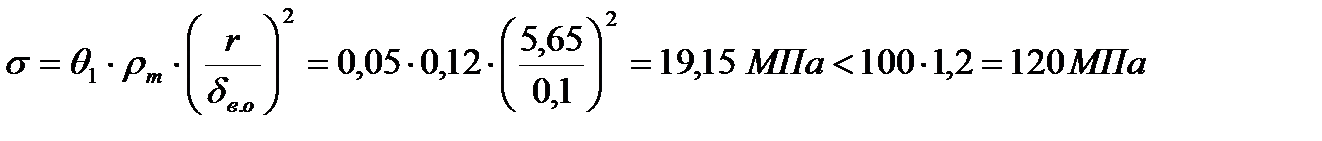 .
.
б) по касательным напряжениям в обшивке:
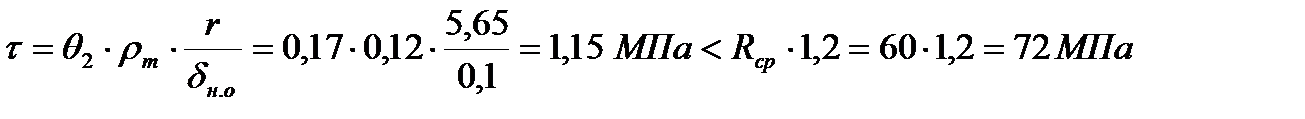 ,
,
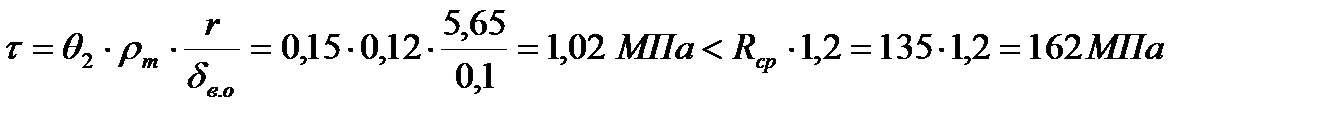
в) по нормальным сжимающим напряжениям в срединном слое:
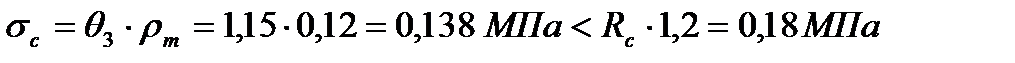 .
.
3.0 Проектирование круговой арки
Трехшарнирные арки являются статически определимыми системами, поэтому определение усилий в них не вызывает каких-либо трудностей. Весь статический расчет будем производить в следующей последовательности:
1. выбор геометрической схемы;
2. подсчет нагрузок и выявление характера их действия;
3. определение усилий в сечениях и составление сводной таблицы усилий.
Выбор геометрической схемы.
За геометрическую схему, а в равной степени и за расчетную схему арки принимают линию, соединяющую центры тяжести сечений, т.е. геометрическую ось арки (рис.2).
Для арки с затяжкой геометрический расчет сводится к следующему.
При известной величине пролета l =42 м. и принятой стреле подъема f =6 м. радиус кривизны r арки кругового очертания определяется по формуле

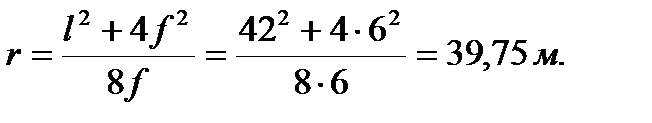
Центральный угол раскрытия 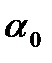 выполняется по формуле
выполняется по формуле
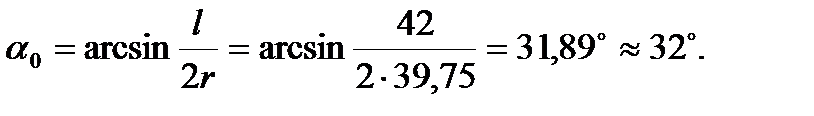
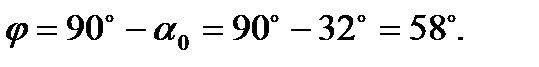
Длину дуги арки S определим выражением
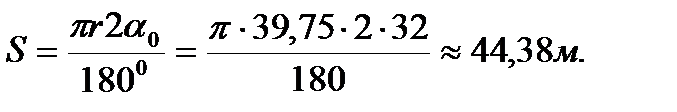
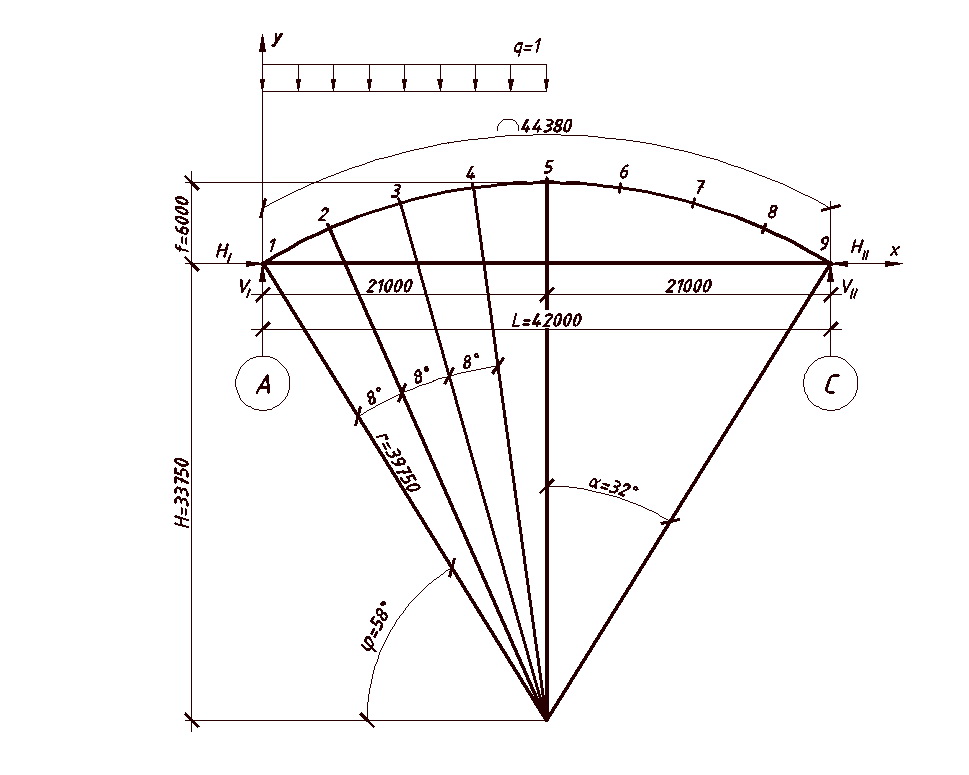
Рис.2 Расчетная схема арки
Подсчет нагрузок.
1. Постоянная нагрузка от покрытия подсчитывается по фактическому весу всех элементов (обшивок, обрамления и среднего слоя) панели. Для возможности дальнейшего сравнения нескольких вариантов в расчетах будем использовать нормативное значение нагрузки 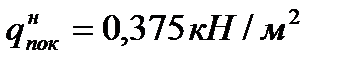 и с учетом коэффициента надежности расчетное значение
и с учетом коэффициента надежности расчетное значение 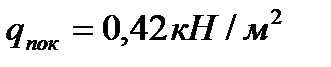 .
.
|
|
2. Снеговую нагрузку будем подсчитывать по [10].
Вариант 1. При равномерно распределенной снеговой нагрузке интенсивностью
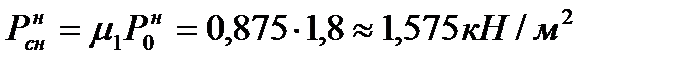
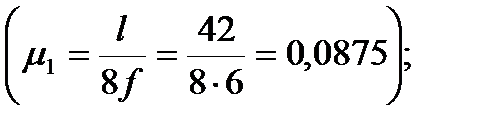
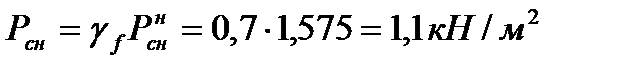
(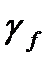 =1,6–коэффициент надежности по нагрузке, согласно [10] при
=1,6–коэффициент надежности по нагрузке, согласно [10] при 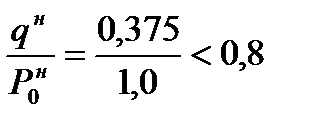 ).
).
Вариант 2. При распределенной по треугольнику треугольной нагрузке с максимальной ординатой
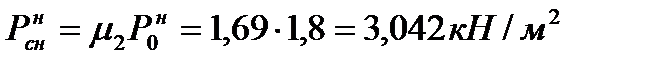
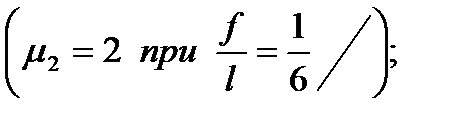
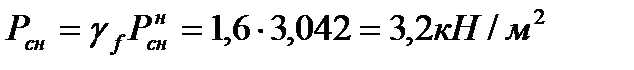
3. Ветровая нагрузка определяется по [10].
Характер действия ветровой нагрузки показан на рис.2.
Интенсивность ветровой нагрузки подсчитывается по формулам:
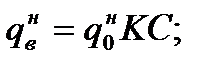
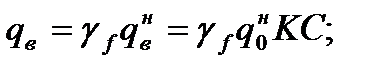
где 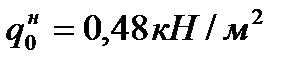 – скоростной напор для второго района;
– скоростной напор для второго района;
C–аэродинамический коэффициент;
B–коэффициент, учитывающий изменение скоростного напора по высоте (для местности типа B [10 табл.6] при высоте H=11м. К=0,44; при H=15,2 м. К=0,61; при H=17 м. К=0,68; другие значения К находятся по интерполяции);
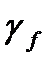 –коэффициент надежности по нагрузке, равный 1,4.
–коэффициент надежности по нагрузке, равный 1,4.
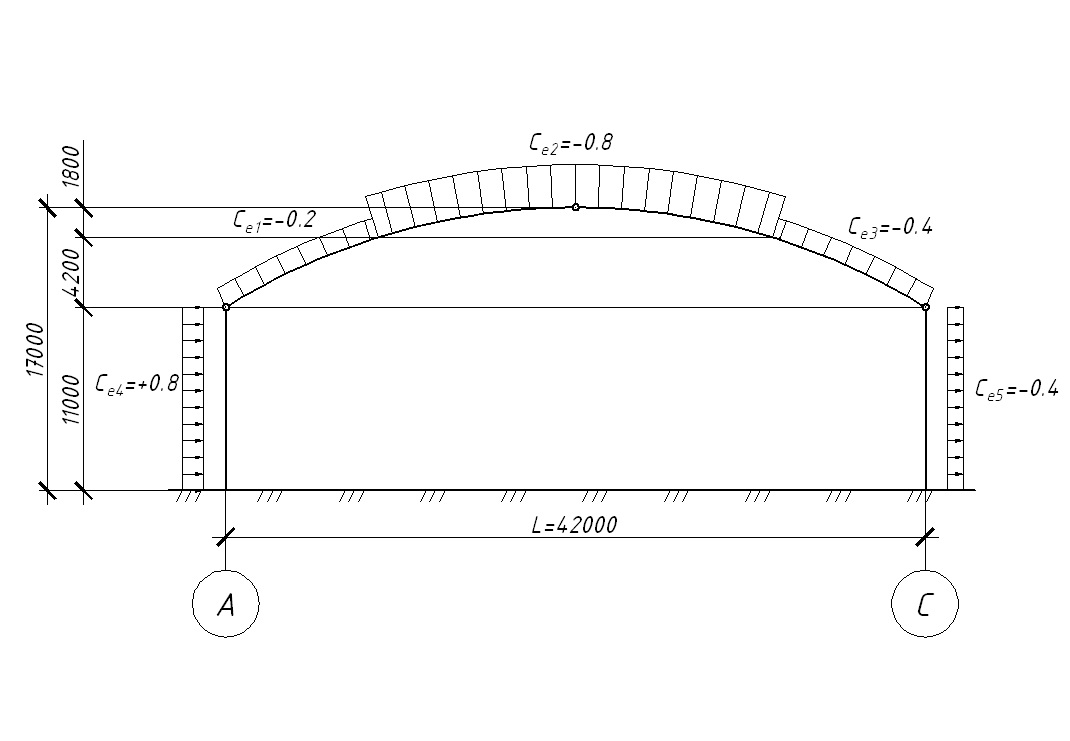
Рис.3 Схема ветровой нагрузки на арку.
Для каждой зоны (см. рис.3) принимаем средние значения коэффициентов Ci и Ki.
При 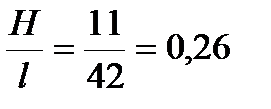 и
и 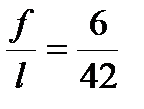 имеем Ce1= -0,2; Ce2= -0,8; Ce3= -0,4.
имеем Ce1= -0,2; Ce2= -0,8; Ce3= -0,4.
Другие коэффициенты показаны на рис.16.
4. Собственный вес арки подсчитываем по формуле
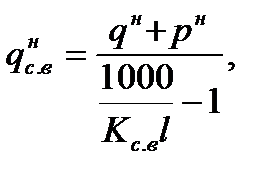
где qн и pн – соответственно постоянная (вес покрытия) и временная (снег) нагрузки, действующие на арку;
Kс.в – коэффициент собственного веса, для арки принимаем равным 4.
Величина распределенной нагрузки от собственного веса:
– нормативная

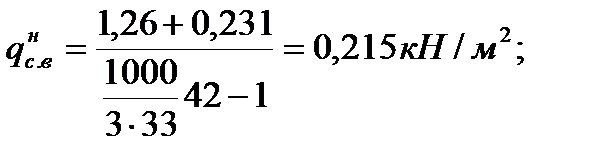
– расчетная
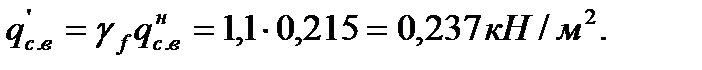
На 1 м2 горизонтальной проекции
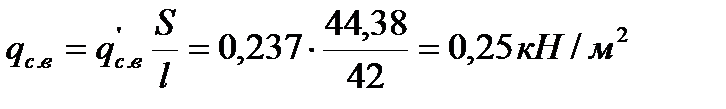
Погонные нагрузки на арку при шаге 6 м.:
– постоянная
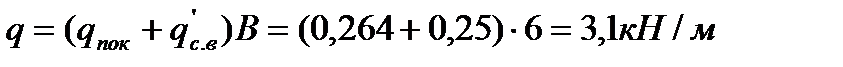
– снеговая:
Вариант 1
|
|
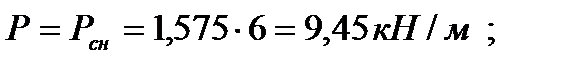
Вариант 2
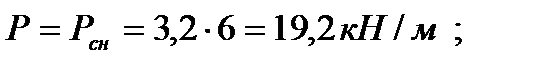
– ветровая:
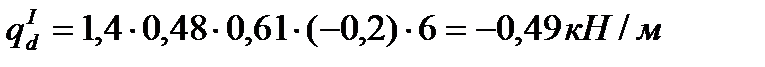
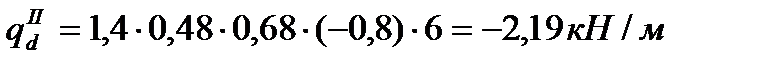
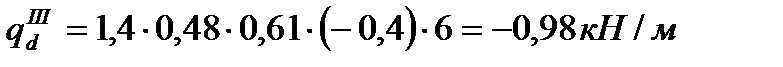
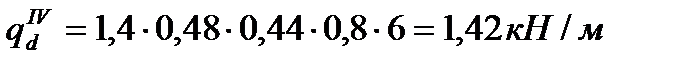
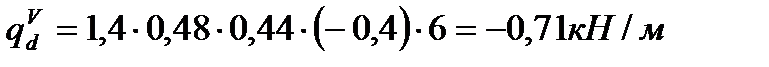
Полная расчетная схема рамы дана на л. 1.