II. Случайные процессы
Лекция 5. Определение и классификация случайных процессов по характеру реализаций и по свойствам их вероятностных распределений
Если некоторая переменная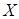 
зависит от скалярного аргумента 
и при каждом фиксированном значении последнего является случайной величиной, то переменную 
называют случайной функцией.
Если аргументом t у переменной является время, то такую случайную функцию называют случайным процессом. Например:
угол тангажа 
летательного аппарата, движущегося в турбулентной атмосфере, является случайным процессом;
движение центра масс летательного аппарата по траектории при действии случайных факторов характеризуется шестимерным вектором 
и представляет собой векторный случайный процесс.
Таким образом случайный процесс (СП) характеризуется тем, что какая-либо физическая величина изменяется во времени, причем это изменение управляется вероятностными законами. Конкретный вид СП (т. е, его фактическая запись в виде файла или осциллограммы) в определенном опыте называется реализацией случайного процесса. В качестве синонимов употребляются также термины траектория случайного процесса и выборочная функция.
Случайная функция может зависеть не от одного, а от нескольких аргументов (например, скорость ветра зависит от времени и пространственных координат). Случайные функции такого характера принято называть случайными полями.
В зависимости от размерности случайных процессов и полей можно ввести следующую классификацию:
1) скалярный случайный процесс - случайный процесс, область значений которого есть множество в пространстве действительных чисел;
2) векторный случайный процесс —случайный процесс, область значений которого есть множество в соответствующем координатном пространстве;
3) скалярное случайное поле 
— случайное поле, область значений которого есть множество из действительных чисел;
4) векторное случайное поле —случайный процесс, представимый в виде компонент, являющихся скалярными полями.
Случайные процессы и соответствующие им случайные функции можно классифицировать по разным признакам:
1) по характеру реализаций 
, т. е, в зависимости от возможных значений, принимаемых случайной функцией и аргументом ;
2) по виду отдельных вероятностных характеристик, используемых для описания СП.
Приведем классификацию по первому признаку (классификация по второму признаку будет дана ниже).
Классификация случайных процессов по характеру реализаций
В зависимости от того, непрерывное или дискретное множество значений принимают и его параметр, можно различать следующие основные виды СП.
1. 
Дискретная случайная последовательность (дискретный процесс с дискретным временем) - СП, у которого область значений и область определения—дискретные множества. В данном случае время t пробегает дискретный ряд значений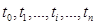 
, а СВ 
может принимать лишь дискретное множество значений 
. Множества значений 
и 
могут быть конечными или бесконечными; в последнем случае 
, 
.
Процессы такого вида непосредственно встречаются на практике (случайное подбрасывание монеты, радиотелеграфия, радиолокация и др.), а также могут быть получены квантованием по уровню и по времени непрерывно изменяющихся процессов с непрерывным временем (рис. 5.1). Такое квантование часто применяется при цифровой обработке различной информации.
2. 
Случайная последовательность (непрерывнозначный процесс с дискретным временем) - СП, у которого область значений— непрерывное множество, а область определения - дискретное.
Такой процесс отличается от процесса первого вида лишь тем, что теперь случайная величина , (
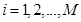) может принимать бесконечное число значений. В качестве примера можно указать временные выборки из непрерывного случайного процесса (рис. 5.2).
3. 
Дискретный случайный процесс
(дискретный процесс с непрерывным временем) - СП, у которого область значений — дискретное множество, а область определения — непрерывное множество. В этом случае может принимать дискретные значения , а время t —континуум значений: 
, где Т —длина временного интервала, на котором задан процесс . Примерами могут служить показания счетчика числа случайно появляющихся частиц, результат квантования непрерывного случайного процесса только по уровню и др. (рис. 5.3).
4. Непрерывнозначный случайный процесс - СП, область значений и область определения
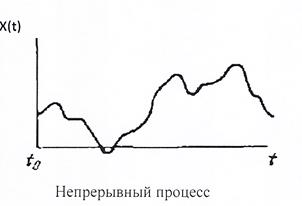
которого - непрерывные множества. В данном случае принимает значения из некоторого непрерывного пространства и аргумент t изменяется также непрерывно, причем реализации процесса могут иметь разрывы первого рода. Если подобные скачки отсутствуют, то такой процесс называется непрерывным (рис. 5.4).
Процесс называется комплексным, если он принимает комплексные значения.
5. Случайный точечный процесс (поток) представляет собой последовательность точек, расположенных случайным образом, например, на оси времени (рис. 5.5).
Такие точки могут соответствовать различным событиям (например» моментам времени наступления отказов в какой-либо системе или аппаратуре, временам поступления требований или заявок на обслуживание и др.).
Помимо пяти указанных видов возможны разнообразные, болеесложные, смешанные виды случайных процессов.
Классификация случайных полей является более разнообразной в зависимости от разных комбинаций характера областей значений, принимаемых как компонентами самого поля , так и компонентами вектора 
и времени .
Классификация случайных процессов по свойствам их вероятностных распределений
Статистическое описание случайного процесса осуществляют, рассматривая множество случайных величин 
, соответствующих различным значениям времени t, взятым на рассматриваемом интервале его изменения 
. Считается, что произвольный случайный процесс описан полностью, если указан способ построения последовательности плотностей вероятности 
при 
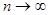, где 
.
Одномерная плотность 
позволяет определить вероятность попадания случайной величины x(t) в интервал 
:
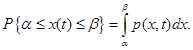
С помощью двумерной совместной плотности 
определяют, с какой вероятностью две случайные величины 
и 
попадут в интервалы 
и 
, соответствующие моментам 
и 
:
Аналогично определяются вероятности для любого n.
Для описания случайных процессов могут также использоваться условные плотности распределения вероятностей. Условная плотность вероятности 
характеризует распределение вероятностей случайной величины 
, реализации которой в момент 
прошли через точку 
. Аналогично условная плотность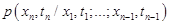 
есть плотность распределения вероятностей случайной величины 
, реализации которой в предшествующие моменты 
принимали фиксированные значения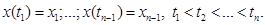 
С учетом соотношений для плотностей векторных случайных величин справедливы следующие соотношения между совместными безусловными и условными распределениями:
(5.1)
Имеют место следующие предельные свойства безусловных и условных распределений:
(5.2)
(5.3)
где 
- дельта-функция в точке .
Дельта-функция относится к так называемым обобщенным функциям. Основные свойства дельта-функции:
1. 
2. 
3. 
Свойство 3 называется фильтрующим свойством дельта-функции.
В другом предельном случае
(5.4)
(5.5)
Теперь приведем соответствующую классификацию.
Абсолютно случайный процесс. Процесс x(t) называют абсолютно случайным, если случайные величины и независимы при сколь угодно малом 
. Для такого процесса совместное 
-мерное распределение при любом п определяется соотношением
(5.6)
т. е. абсолютно случайный процесс полностью описывается его одномерным распределением , известным для каждого .
Марковский процесс. Зададим на интервале возможного изменения аргумента случайного процесса временной ряд 
. Случайный процесс x(t) называют марковским, если для него справедливо соотношение для любых 
:
(5.7)
Для марковского процесса условная плотность вероятности случайной величины зависит только от того, каким было значение случайной величины 
и никак не зависит от того, каким были реализации 
данного процесса в предыдущие моменты 
. Плотность 
называют также переходной плотностью вероятности марковского процесса x(t).
Для марковского процесса x(t), учитывая (5.1) и (5.7), имеем
(5.8)
Как видим, для исчерпывающего описания марковского случайного процесса достаточно задать его начальную одномерную плотность вероятности 
и переходные плотности 
.
Марковский процесс с независимыми приращениями. Случайный процесс называют процессом с независимыми приращениями, если для любых значений 
, выбранных на интервале , приращения 
— независимые случайные величины. Процесс с независимыми приращениями — также марковский, так как значение случайной величины 
в конце каждого интервала 
определяется предыдущим значением 
и приращением на этом интервале, не зависящим от приращений на предшествующих интервалах.
Гауссовский случайный процесс. Случайный процесс x(t), у которого совместная
-мерная плотность вероятности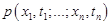 
при любом п и любых 
является гауссовской, называется гауссовским случайным процессом.
Лекция 6. Корреляционная теория случайных процессов. Мат. ожидание и корреляционная функция; стационарные случайные процессы, эргодическое свойство, белый шум.
При практических расчетах для описания случайных процессов, как и для описания случайных величин, часто пользуются их моментными или числовыми характеристиками.
В отличие от числовых характеристик случайных величин, представляющих собой определенные числа, характеристики случайных функций представляют собой в общем случае не числа, а функции.
Простейшей моментной (числовой) характеристикой случайного процесса является математическое ожидание 
, представляющее собой неслучайную функцию времени t. Если известна одномерная плотность вероятности , то можно рассчитать для каждого t по формуле:
(6.1)
Математическим ожиданием случайного процесса называется неслучайная функция 
которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайного процесса.
На рис. 6.1 тонкими линиями показаны реализации случайного процесса, жирной линией - его математическое ожидание.
Аналогичным образом определяется дисперсия случайного процесса.
Дисперсией случайного процесса ) называется неслучайная функция Dx(t), значение которой для каждого t равно дисперсии соответствующего сечения случайного процесса.
Дисперсия Dx(t) случайного процесса характеризует рассеивание возможных реализаций процесса в окрестности его математического ожидания и определяется по формуле
Математическое ожидание и дисперсия 
характеризуют лишь среднее течение и разброс возможных реализаций случайного процесса по времени. Они не содержит в себе информацию о степени статистической взаимосвязи (корреляции) возможных реализаций процесса в различные моменты времени.
Действительно, рассмотрим два случайных процесса 
и 
возможные реализации которых приведены на рис. 6.2 и 6.3 соответственно
Математические ожидания и дисперсии этих процессов одинаковы, однако, характер траекторий различный. Процесс имеет более плавные, более «предсказуемые» траектории, в то время как траектории процесса более изменчивые, менее «предсказуемые». Поэтому для описания вероятностной зависимости между возможными реализациями случайного процесса в различные моменты времени используют его корреляционную функцию. Она представляет собой неслучайную функцию 
двух аргументов и , определяемую следующим образом:
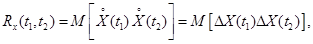(6.2)
где 
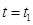- центрированные случайные величины (центрированные сечения случайного процесса), соответствующие значениям при 
и 
.
Таким образом, корреляционная функция случайного процесса - это взаимный корреляционный момент 
между случайными величинами (сечениями) 
и 
, зависящий от аргументов и .
Если совместная двумерная плотность 
случайного процесса x(t) известна, то корреляционную функцию данного процесса можно определить с помощью соотношения:
(6.3)
По имеющимся реализациям 
оценку 
корреляционной функции можно рассчитать с помощью формулы математической статистики
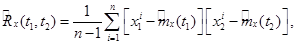(6.4)
где 
, причем 
Если аргументы и в корреляционной функции совпадают, т. е.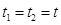 
, то, учитывая предельное свойство (5.2), из соотношения (6.3) получаем
(6.5)
Таким образом, корреляционная функция при совпадающих аргументах есть не что иное, как дисперсия случайной величины 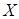, получаемой из случайного процесса путем фиксации аргумента . Поэтому необходимость в дисперсии как отдельной характеристике случайного процесса отпадает: в качестве основных характеристик случайного процесса достаточно рассматривать его математическое ожидание и корреляционную функцию.
На рис. 6.4 изображена корреляционная функция в виде поверхности. Эта поверхность симметрична относительно вертикальной плоскости, проходящей через биссектрису угла 
.
Корреляционную функцию , отнесенную к произведению 
, называют нормированной корреляционной функцией
. (6.6)
При 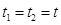нормированная корреляционная функция 
равна единице. Равенство нулю или 
указывает на отсутствие корреляции между возможными реализациями случайного процесса x(t) в моменты и . Как правило, по мере увеличения интервала 
корреляция между возможными реализациями случайного процесса x(t) убывает. Корреляционная функция процесса при этом меняется от 
до нуля, а - от 1 до 0.
Результат усреднения в (6.3) не зависит от того, в какой последовательности рассматриваются 
и 
, поэтому корреляционная функция не меняется при перемене аргументов местами: 
.
Изучение свойств случайных процессов на уровне их первых двух моментов (математического ожидания mx(t) и корреляционной функции называют корреляционной теорией случайных процессов. В рамках корреляционной теории случайный процесс описывается полностью, если этот процесс – гауссовский.
Корреляционная теория распространяется и на векторные случайные процессы. Если векторный процесс, объединяющий п компонент 
, то в рамкахкорреляционной теории этот процесс описывается вектором математических ожиданий
и матричной корреляционной функцией
где - центрированные случайные векторы. Диагональные элементы 
, 
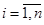матричной корреляционной функции называют автокорреляционными функциями соответствующих компонент векторного случайного процесса x(t), а внедиагональные 
- взаимными корреляционными функциями компонент 
и 
.
При 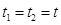матричная корреляционная функция векторного случайного процесса обращается в его ковариационную матрицу 
, характеризующую линейную вероятностную зависимость между компонентами вектора 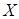в момент времени t.
Стационарные случайные процессы (сильная и слабая стационарность).
Говорят, что случайный процесс (скалярный или векторный) стационарен в узком смысле или сильно стационарен, если любая его -мерная плотность вероятности (или функция распределения) инвариантна относительно временного сдвига
. (6.7)
Случайный процесс (скалярный или векторный), у которого математическое ожидание постоянно, а корреляционная функция зависит не от самих значений аргументов и , а от их разности , т. е.
, (6.8)
называют слабо стационарным случайным процессом, или стационарным в широком смысле.
Из стационарности в узком смысле следует стационарность в широком смысле, но не наоборот.
Дисперсия стационарного случайного процесса 
постоянна. Интервал 
за пределами которого корреляционная функция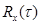 
не превосходит некоторую установленную малую величину, называют временем корреляции процесса . Величина 
является простейшей количественной мерой степени коррелированности значений случайного процесса по времени.
Эргодическое свойство. Для определения математического ожидания и корреляционной функции стационарного случайного процесса по экспериментальным данным следует пользоваться формулами математической статистики, подставляя в них значения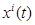 
различных реализаций процесса в соответствующие моменты времени. Однако, в некоторых случаях результаты расчетов не изменятся, если в эти формулы подставлять значения 
одной достаточно длинной реализации 
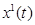случайного процесса в различные моменты времени. Про стационарные случайные процессы, для которых такая замена справедлива, говорят, что они обладают эргодическим свойством.
Случайный процесс X (t) называют эргодическим, если все его статистические свойства могут быть определены по одной единственной реализации .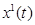
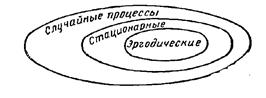
Соотношение между различными видами случайных процессов показаны на рис. 6.5.
Рис. 6.5
Необходимым и достаточным условием эргодичности стационарного случайного процесса является выполнение равенства
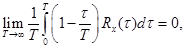(6.9)
а достаточным – выполнение более простого условия
(6.10)
Для расчета математического ожидания тх и корреляционной функции 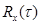стационарного случайного процесса , обладающего свойством эргодичности, можно пользоваться соотношениями для 
.
(6.11)
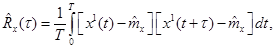(6.12)
где 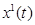- одна длинная реализация процесса; 
.
При проведении расчетов на ЦВМ эти интегралы заменяют конечными суммами
(6.13)
(6.14)
Белый шум. Так, в рамках корреляционной теории определяют случайный процесс , значения которого и некоррелированы при сколь угодно малом . Можно показать, что некоррелированность значений случайного процесса в моменты и при сколь угодно малом может быть обеспечена лишь в том случае, когда его корреляционная функция имеет вид
(6.15)
где 
- дельта-функция в точке .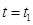
Множитель 
называют интенсивностью белого шума, которая определяется как предел
У стационарного белого шума интенсивность N постоянна во времени. Если 
, то стационарный белый шум называют стандартным. Из определения дельта-функции следует, что дисперсия белого шума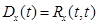 
равна бесконечности. Это означает, что физически белый шум не может быть реализован точно и может рассматриваться лишь как абстракция - результат предельного перехода коррелированного случайного процесса при 
Векторный белый шум , состоящий из п компонент, характеризуется матрицей интенсивностей 
Диагональные элементы 
этой матрицы суть интенсивности отдельных составляющих векторного белого шума, а внедиагональные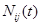 
- взаимные интенсивности, характеризующие корреляцию между различными составляющими векторного белого шума в один и тот же момент времени. Наиболее часто рассматривают случай, когда все составляющие векторного белого шума некоррелированные. В этом случае матрица N(t) диагональная.
Понятие белого шума находит широкое применение при решении многих задач статистического анализа и оптимизации управления движением летательных аппаратов.
Лекция 7. Канонические разложения случайных процессов. Спектральная плотность стационарного случайного процесса. Примеры: белый шум, экспоненциально коррелированный процесс
В некоторых случаях для описания случайного процесса применяют его представление через сумму случайных процессов более простого вида. Один из способов такого представления называется каноническим разложением. При каноническом разложении случайный процесс представляют в виде
(7.1)
где - математическое ожидание процесса;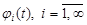 
- координатные функции, являющиеся заданными неслучайными функциями времени; 
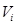- коэффициенты, являющиеся некоррелированными случайными величинами с нулевыми математическими ожиданиями и дисперсиями 
В качестве координатных функций в канонических разложениях используют семейства функций, обладающих свойством ортонормированности:
Корреляционная функция случайного процесса (6.2) выражается через его каноническое разложение:
(7.2)
Суммирование по переменной 
исчезает, поскольку 
вследствие некоррелированности случайных величи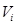и и 
.
При 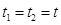из (7.2) получаем выражение для дисперсии
(7.3)
При практических расчетах ограничиваются конечным числом членов канонического разложения. Методика построения канонических разложений случайных процессов изложена в книге [5].
Спектральная плотность. Наряду с корреляционной функцией для статистического описания стационарных случайных процессов используют спектральную плотность 
. Так называют функцию частоты 
, являющуюся обратным интегральным преобразованием Фурье от корреляционной функции 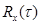случайного процесса :
(7.4)
В свою очередь, корреляционная функция процесса выражается через его спектральную плотность как прямое интегральное преобразование Фурье:
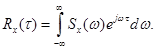(7.5)
Отсюда при 
получаем выражение для дисперсии стационарного случайного процесса:
(7.6)
Используя тригонометрическую форму представления комплексных переменных
получаем
(7.7)
Свойства спектральной плотности
1. Неотрицательность:
2. Интеграл от спектральной плотности в бесконечных пределах равен дисперсии СП:
3. - чётная функция:
При описании стационарных случайных процессов вместо может задаваться спектральная плотность, определяемая для положительных частот:
(7.8)
В этом случае корреляционная функция процесса должна вычисляться по известной спектральной плотности 
с помощью соотношения
(7.9)
а дисперсия 
определяется с помощью формулы
(7.10)
Последнее выражение позволяет дать физическую интерпретацию спектральной плотности : она характеризует плотность распределения дисперсии стационарного случайн