Задания по геометрии в форме огэ

1. В тре­уголь­ни­ке ABC AC = BC. Внеш­ний угол при вер­ши­не B равен 146°. Най­ди­те угол C. Ответ дайте в гра­ду­сах.

2. Ка­те­ты пря­мо­уголь­но­го тре­уголь­ни­ка равны и 1. Най­ди­те синус наи­мень­ше­го угла этого тре­уголь­ни­ка.

3. 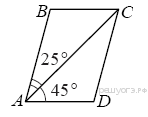Диа­го­наль AC па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 45° и 25°. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма.

4. Бис­сек­три­са угла A па­рал­ле­ло­грам­ма ABCD пе­ре­се­ка­ет сто­ро­ну BC в точке K. Най­ди­те пе­ри­метр па­рал­ле­ло­грам­ма, если BK = 7, CK = 12.

5. 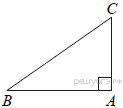В тре­уголь­ни­ке ABC угол A равен 90°, AC = 6, sin B = 0,3. Най­ди­те BC.

6. На пря­мой AB взята точка M. Луч MD — бис­сек­три­са угла CMB. Из­вест­но, что ∠ DMC = 60°. Най­ди­те угол CMA. Ответ дайте в гра­ду­сах.

7. Сумма двух углов рав­но­бед­рен­ной тра­пе­ции равна 140°. Най­ди­те боль­ший угол тра­пе­ции. Ответ дайте в гра­ду­сах.

8. Диа­го­наль BD па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 50° и 85°. Най­ди­те мень­ший угол па­рал­ле­ло­грам­ма.

9. Четырёхуголь­ник ABCD впи­сан в окруж­ность. Угол ABD равен 71°, угол CAD равен 61°. Най­ди­те угол ABC. Ответ дайте в гра­ду­сах.

10. В тре­уголь­ни­ке ABC угол C пря­мой, BC = 3, cos B = 0,6. Най­ди­те AB.

11. В тре­уголь­ни­ке ABC про­ве­де­ны ме­ди­а­на BM и вы­со­та BH. Из­вест­но, что AC = 84 и BC = BM. Най­ди­те AH.

12. В пря­мо­уголь­ном тре­уголь­ни­ке ABC катет AC = 70, а вы­со­та CH, опу­щен­ная на ги­по­те­ну­зу, равна . Най­ди­те .

13. Четырёхуголь­ник ABCD впи­сан в окруж­ность. Угол ABD равен 19°, угол CAD равен 35°. Най­ди­те угол ABC. Ответ дайте в гра­ду­сах.

14. 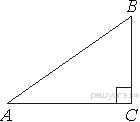В тре­уголь­ни­ке ABC угол C равен 90°, AC = 4, tg A = 0,75. Най­ди­те BC.

15. Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна Один из ост­рых углов равен 30°. Най­ди­те длину ка­те­та, ле­жа­ще­го на­про­тив этого угла.

16. Два ост­рых угла пря­мо­уголь­но­го тре­уголь­ни­ка от­но­сят­ся как 4:5. Най­ди­те боль­ший ост­рый угол. Ответ дайте в гра­ду­сах.

17. Пря­мые m и n па­рал­лель­ны. Най­ди­те ∠3, если ∠1 = 22°, ∠2 = 72°. Ответ дайте в гра­ду­сах.

18. Бо­ко­вая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 10, а ос­но­ва­ние равно 12. Най­ди­те пло­щадь этого тре­уголь­ни­ка.

19. Четырёхуголь­ник ABCD впи­сан в окруж­ность. Угол ABD равен 14°, угол CAD равен 30°. Най­ди­те угол ABC. Ответ дайте в гра­ду­сах.

20. В тра­пе­ции ABCD AB = CD, ∠ BDA = 49° и ∠ BDC = 13°. Най­ди­те угол ABD. Ответ дайте в гра­ду­сах.

21. Сто­ро­на AC тре­уголь­ни­ка ABC про­хо­дит через центр опи­сан­ной около него окруж­но­сти. Най­ди­те ∠ C, если ∠ A = 75°. Ответ дайте в гра­ду­сах.

22. Два угла впи­сан­но­го в окруж­ность че­ты­рех­уголь­ни­ка равны 82° и 58°. Най­ди­те боль­ший из остав­ших­ся углов. Ответ дайте в гра­ду­сах.

23. Точка O — центр окруж­но­сти, на ко­то­рой лежат точки S, T и V таким об­ра­зом, что OSTV — ромб. Най­ди­те угол STV. Ответ дайте в гра­ду­сах.

24. Най­ди­те ве­ли­чи­ну остро­го угла па­рал­ле­ло­грам­ма ABCD, если бис­сек­три­са угла A об­ра­зу­ет со сто­ро­ной BC угол, рав­ный 15°. Ответ дайте в гра­ду­сах.

25. В тре­уголь­ни­ке ABC угол C пря­мой, BC = 8, sin A = 0,4. Най­ди­те AB.

26. В вы­пук­лом че­ты­рех­уголь­ни­ке ABCD AB = BC, AD = CD, ∠ B = 77°, ∠ D = 141°. Най­ди­те угол A. Ответ дайте в гра­ду­сах.

27. Сумма трех углов вы­пук­ло­го че­ты­рех­уголь­ни­ка равна 300°. Най­ди­те чет­вер­тый угол. Ответ дайте в гра­ду­сах.

28. В тре­уголь­ни­ке угол равен 90°, . Най­ди­те .

29. В пря­мо­уголь­ном тре­уголь­ни­ке ABC катет AC = 75, а вы­со­та CH, опу­щен­ная на ги­по­те­ну­зу, равна Най­ди­те

30. Тан­генс остро­го угла пря­мо­уголь­ной тра­пе­ции равен Най­ди­те её боль­шее ос­но­ва­ние, если мень­шее ос­но­ва­ние равно вы­со­те и равно 15.

31. 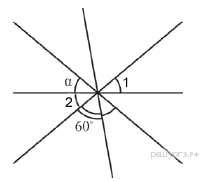Углы, от­ме­чен­ные на ри­сун­ке одной дугой, равны. Най­ди­те угол α. Ответ дайте в гра­ду­сах.

32. В тре­уголь­ни­ке ABC угол C равен 90°, BC = 20, = 0,5. Най­ди­те AC.

33. Най­ди­те ве­ли­чи­ну угла DOK, если OK — бис­сек­три­са угла AOD, ∠ DOB = 108°. Ответ дайте в гра­ду­сах.

34. В рав­но­бед­рен­ной тра­пе­ции из­вест­ны вы­со­та, мень­шее ос­но­ва­ние и угол при ос­но­ва­нии. Най­ди­те боль­шее ос­но­ва­ние.

35. Най­ди­те угол АВС рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной CD углы, рав­ные 20° и 100° со­от­вет­ствен­но.

36. Бис­сек­три­сы углов A и B при бо­ко­вой сто­ро­не AB тра­пе­ции ABCD пе­ре­се­ка­ют­ся в точке F. Най­ди­те AB, если AF = 24, BF = 32.

37. В рав­но­бед­рен­ном тре­уголь­ни­ке ABC с ос­но­ва­ни­ем AC внеш­ний угол при вер­ши­не C равен 123°. Най­ди­те ве­ли­чи­ну угла ВАС. Ответ дайте в гра­ду­сах.

38. В тре­уголь­ни­ке угол равен 90°, 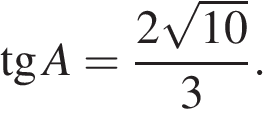Най­ди­те

39. Пря­мые m и n па­рал­лель­ны. Най­ди­те ∠3, если ∠1= 19°, ∠2 = 82°. Ответ дайте в гра­ду­сах.

40. В пря­мо­уголь­ном тре­уголь­ни­ке катет 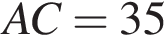, а вы­со­та , опу­щен­ная на ги­по­те­ну­зу, равна Най­ди­те

41. Раз­ность углов, при­ле­жа­щих к одной сто­ро­не па­рал­ле­ло­грам­ма, равна 40°. Най­ди­те мень­ший угол па­рал­ле­ло­грам­ма. Ответ дайте в гра­ду­сах.

42. В тре­уголь­ни­ке = 35, угол равен 90°. Най­ди­те ра­ди­ус опи­сан­ной окруж­но­сти этого тре­уголь­ни­ка.

43. В тре­уголь­ни­ке ABC угол C равен 90°, AC = 20, tg A = 0,5. Най­ди­те BC.

44. 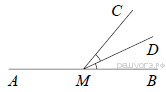На пря­мой AB взята точка M. Луч MD — бис­сек­три­са угла CMB. Из­вест­но, что ∠ DMC = 44°. Най­ди­те угол CMA. Ответ дайте в гра­ду­сах.

45. Най­ди­те мень­ший угол рав­но­бед­рен­ной тра­пе­ции, если два ее угла от­но­сят­ся как 1:2. Ответ дайте в гра­ду­сах.

46. В тре­уголь­ни­ке ABC угол C равен 90°, BC = 6, sin A = 0,3. Най­ди­те AB.

47. В тре­уголь­ни­ке ABC угол C равен 90°, BC = 12, tg A = 1,5. Най­ди­те AC.

48. В тра­пе­ции ABCD AB = CD, AC = AD и ∠ ABC = 95°. Най­ди­те угол CAD. Ответ дайте в гра­ду­сах.

49. Один угол па­рал­ле­ло­грам­ма в два раза боль­ше дру­го­го. Най­ди­те мень­ший угол. Ответ дайте в гра­ду­сах.

50. Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 36, а ос­но­ва­ние равно 16. Най­ди­те пло­щадь тре­уголь­ни­ка.

51. Точка О — центр окруж­но­сти, ∠ AOB = 84° (см. ри­су­нок). Най­ди­те ве­ли­чи­ну угла ACB (в гра­ду­сах).

52. Длина хорды окруж­но­сти равна 96, а рас­сто­я­ние от цен­тра окруж­но­сти до этой хорды равно 20. Най­ди­те диа­метр окруж­но­сти.

53. К окруж­но­сти с цен­тром в точке О про­ве­де­ны ка­са­тель­ная AB и се­ку­щая AO. Най­ди­те ра­ди­ус окруж­но­сти, если AB = 14 см, AO = 50 см.

54. Че­ты­рех­уголь­ник ABCD впи­сан в окруж­ность. Угол ABC равен 70°, угол CAD равен 49°. Най­ди­те угол ABD. Ответ дайте в гра­ду­сах.

55. Окруж­ность с цен­тром в точке O опи­са­на около рав­но­бед­рен­но­го тре­уголь­ни­ка ABC, в ко­то­ром AB = BC и ∠ ABC = 66°. Най­ди­те ве­ли­чи­ну угла BOC. Ответ дайте в гра­ду­сах.

56. Ве­ли­чи­на цен­траль­но­го угла AOD равна 110°. Най­ди­те ве­ли­чи­ну впи­сан­но­го угла ACB. Ответ дайте в гра­ду­сах.

57. Пря­мая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окруж­но­сти. Хорда KM об­ра­зу­ет с ка­са­тель­ной угол, рав­ный 60°. Най­ди­те ве­ли­чи­ну угла OMK. Ответ дайте в гра­ду­сах.

58. От­ре­зок AB = 48 ка­са­ет­ся окруж­но­сти ра­ди­у­са 14 с цен­тром O в точке B. Окруж­ность пе­ре­се­ка­ет от­ре­зок AO в точке D. Най­ди­те AD.

59. Най­ди­те ве­ли­чи­ну (в гра­ду­сах) впи­сан­но­го угла α, опи­ра­ю­ще­го­ся на хорду AB, рав­ную ра­ди­у­су окруж­но­сти.

60. 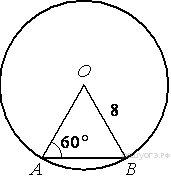Цен­траль­ный угол AOB опи­ра­ет­ся на хорду АВ так, что угол ОАВ равен 60°. Най­ди­те длину хорды АВ, если ра­ди­ус окруж­но­сти равен 8.

61. От­рез­ки AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 23°. Най­ди­те угол AOD. Ответ дайте в гра­ду­сах.

62. 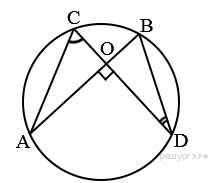Точки A, B, C и D лежат на одной окруж­но­сти так, что хорды AB и СD вза­им­но пер­пен­ди­ку­ляр­ны, а ∠ BDC = 25°. Най­ди­те ве­ли­чи­ну угла ACD.

63. Точка O – центр окруж­но­сти, на ко­то­рой лежат точки A, B и C. Из­вест­но, что ∠ ABC = 15° и ∠ OAB = 8°. Най­ди­те угол BCO. Ответ дайте в гра­ду­сах.

64. Ра­ди­ус окруж­но­сти с цен­тром в точке O равен 65, длина хорды AB равна 126. Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k.

65. На окруж­но­сти с цен­тром O от­ме­че­ны точки A и B так, что ∠ AOB = 66°. Длина мень­шей дуги AB равна 99. Най­ди­те длину боль­шей дуги.

66. Пря­мая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окруж­но­сти. Хорда KM об­ра­зу­ет с ка­са­тель­ной угол, рав­ный 83°. Най­ди­те ве­ли­чи­ну угла OMK. Ответ дайте в гра­ду­сах.

67. В угол C ве­ли­чи­ной 107° впи­са­на окруж­ность, ко­то­рая ка­са­ет­ся сто­рон угла в точ­ках A и B. Най­ди­те угол AOB. Ответ дайте в гра­ду­сах.

68. В окруж­ность впи­сан рав­но­сто­рон­ний вось­ми­уголь­ник. Най­ди­те ве­ли­чи­ну угла ABC.

69.

В тре­уголь­ни­ке ABC угол C равен 90°, AC = 30, BC = Най­ди­те ра­ди­ус окруж­но­сти, опи­сан­ной около этого тре­уголь­ни­ка.

70. От­рез­ки AB и CD яв­ля­ют­ся хор­да­ми окруж­но­сти. Най­ди­те длину хорды CD, если AB = 20, а рас­сто­я­ния от цен­тра окруж­но­сти до хорд AB и CD равны со­от­вет­ствен­но 24 и 10.

71. 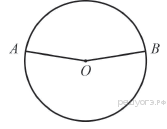Точки A и B делят окруж­ность на две дуги, длины ко­то­рых от­но­сят­ся как 9:11. Най­ди­те ве­ли­чи­ну цен­траль­но­го угла, опи­ра­ю­ще­го­ся на мень­шую из дуг. Ответ дайте в гра­ду­сах.

72. 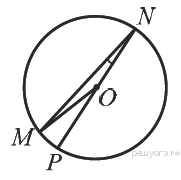Най­ди­те гра­дус­ную меру ∠ MON, если из­вест­но, NP — диа­метр, а гра­дус­ная мера ∠ MNP равна 18°.

73. Ра­ди­ус окруж­но­сти с цен­тром в точке O равен 82, длина хорды AB равна 36. Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k.

74. Пря­мо­уголь­ный тре­уголь­ник с ка­те­та­ми 5 см и 12 см впи­сан в окруж­ность. Чему равен ра­ди­ус этой окруж­но­сти?

75. 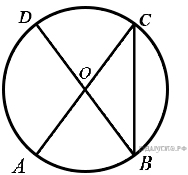В окруж­но­сти с цен­тром O AC и BD — диа­мет­ры. Цен­траль­ный угол AOD равен 112°. Най­ди­те впи­сан­ный угол ACB. Ответ дайте в гра­ду­сах.

76. В окруж­но­сти с цен­тром в точке O про­ве­де­ны диа­мет­ры AD и BC, угол OAB равен 25°. Най­ди­те ве­ли­чи­ну угла OCD.

77. 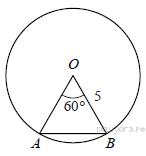Цен­траль­ный угол AOB равен 60°. Най­ди­те длину хорды AB, на ко­то­рую он опи­ра­ет­ся, если ра­ди­ус окруж­но­сти равен 5.

78. Ра­ди­ус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду AC в точке D и пер­пен­ди­ку­ля­рен ей. Най­ди­те длину хорды AC, если BD = 1 см, а ра­ди­ус окруж­но­сти равен 5 см.

79. Окруж­ность впи­са­на в квад­рат. Най­ди­те пло­щадь квад­ра­та.

80. Окруж­ность с цен­тром в точке O опи­са­на около рав­но­бед­рен­но­го тре­уголь­ни­ка ABC, в ко­то­ром AB = BC и ∠ ABC = 177°. Най­ди­те ве­ли­чи­ну угла BOC. Ответ дайте в гра­ду­сах.

81. Бо­ко­вая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 4. Угол при вер­ши­не, про­ти­во­ле­жа­щий ос­но­ва­нию, равен 120°. Най­ди­те диа­метр окруж­но­сти, опи­сан­ной около этого тре­уголь­ни­ка.

82. Цен­траль­ный угол AOB опи­ра­ет­ся на хорду AB дли­ной 6. При этом угол OAB равен 60°. Най­ди­те ра­ди­ус окруж­но­сти.

83. От­рез­ки AB и CD яв­ля­ют­ся хор­да­ми окруж­но­сти. Най­ди­те рас­сто­я­ние от цен­тра окруж­но­сти до хорды CD, если AB = 18, CD = 24, а рас­сто­я­ние от цен­тра окруж­но­сти до хорды AB равно 12.

84. Ка­са­тель­ные в точ­ках A и B к окруж­но­сти с цен­тром O пе­ре­се­ка­ют­ся под углом 24°. Най­ди­те угол ABO. Ответ дайте в гра­ду­сах.

85. AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 79°. Най­ди­те угол AOD. Ответ дайте в гра­ду­сах.

86. В окруж­но­сти с цен­тром O AC и BD — диа­мет­ры. Угол ACB равен 26°. Най­ди­те угол AOD. Ответ дайте в гра­ду­сах.

87. Ра­ди­ус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду MN в её се­ре­ди­не — точке K. Най­ди­те длину хорды MN, если KB = 1 см, а ра­ди­ус окруж­но­сти равен 13 см.

88. На окруж­но­сти по раз­ные сто­ро­ны от диа­мет­ра AB взяты точки M и N. Из­вест­но, что ∠ NBA = 38°. Най­ди­те угол NMB. Ответ дайте в гра­ду­сах.

89. К окруж­но­сти с цен­тром в точке О про­ве­де­ны ка­са­тель­ная AB и се­ку­щая AO. Най­ди­те ра­ди­ус окруж­но­сти, если AB = 12 см, AO = 13 см.

90. Ра­ди­ус окруж­но­сти с цен­тром в точке O равен 85, длина хорды AB равна 102. Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k.

91. Най­ди­те гра­дус­ную меру ∠ACB, если из­вест­но, что BC яв­ля­ет­ся диа­мет­ром окруж­но­сти, а гра­дус­ная мера ∠AOC равна 96°.

92. Тре­уголь­ник ABC впи­сан в окруж­ность с цен­тром в точке O. Най­ди­те гра­дус­ную меру угла C тре­уголь­ни­ка ABC, если угол AOB равен 27°.

93. Най­ди­те пло­щадь квад­ра­та, опи­сан­но­го во­круг окруж­но­сти ра­ди­у­са 7.

94. Точка О — центр окруж­но­сти, ∠ ACB = 24° (см. ри­су­нок). Най­ди­те ве­ли­чи­ну угла AOB (в гра­ду­сах).

95. Тре­уголь­ник ABC впи­сан в окруж­ность с цен­тром в точке O. Най­ди­те гра­дус­ную меру угла C тре­уголь­ни­ка ABC, если угол AOB равен 48°.

96. В окруж­но­сти с цен­тром в точке O про­ве­де­ны диа­мет­ры AD и BC, угол OAB равен 70°. Най­ди­те ве­ли­чи­ну угла OCD.

97. В окруж­но­сти с цен­тром O AC и BD — диа­мет­ры. Цен­траль­ный угол AOD равен 130°. Най­ди­те впи­сан­ный угол ACB. Ответ дайте в гра­ду­сах.

98. От­ре­зок AB = 40 ка­са­ет­ся окруж­но­сти ра­ди­у­са 75 с цен­тром O в точке B. Окруж­ность пе­ре­се­ка­ет от­ре­зок AO в точке D. Най­ди­те AD.

99. Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точке О. Най­ди­те ра­ди­ус окруж­но­сти, если угол между ка­са­тель­ны­ми равен 60°, а рас­сто­я­ние от точки А до точки О равно 8.

100. Тре­уголь­ник ABC впи­сан в окруж­ность с цен­тром в точке О. Най­ди­те гра­дус­ную меру угла C тре­уголь­ни­ка ABC, если угол AOB равен 123°.

101. Сто­ро­на квад­ра­та равна 10. Най­ди­те его пло­щадь.

102. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 15 и 25, а её бо­ко­вые сто­ро­ны равны 13. Най­ди­те пло­щадь тра­пе­ции.

103. Сто­ро­на рав­но­сто­рон­не­го тре­уголь­ни­ка равна 10. Най­ди­те его пло­щадь, делённую на .

104. Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна 6, а синус угла между ней и одним из ос­но­ва­ний равен . Най­ди­те пло­щадь тра­пе­ции.

105. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна 12, а угол между ними равен 30°. Най­ди­те пло­щадь тре­уголь­ни­ка.

106.. Пе­ри­метр ромба равен 40, а один из углов равен 45°. Най­ди­те пло­щадь ромба, делённую на .

107. Тан­генс остро­го угла пря­мо­уголь­ной тра­пе­ции равен . Най­ди­те её бóльшее ос­но­ва­ние, если мень­шее ос­но­ва­ние равно вы­со­те и равно 14.

108. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен , угол, ле­жа­щий на­про­тив него, равен 60°, а ги­по­те­ну­за равна 20. Най­ди­те пло­щадь тре­уголь­ни­ка, делённую на .

109. Вы­со­та рав­но­бед­рен­ной тра­пе­ции, про­ведённая из вер­ши­ны C, делит ос­но­ва­ние AD на от­рез­ки дли­ной 8 и 15. Най­ди­те длину ос­но­ва­ния BC.

110. Ос­но­ва­ния тра­пе­ции равны 3 и 13. Най­ди­те боль­ший из от­рез­ков, на ко­то­рые делит сред­нюю линию этой тра­пе­ции одна из её диа­го­на­лей.

111. Пе­ри­метр ромба равен 40, а один из углов равен 60°. Най­ди­те пло­щадь ромба, делённую на .

112. 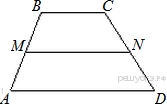В тра­пе­ции ABCD AD = 5, BC = 2, а её пло­щадь равна 28. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

113. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — 10, а угол, из ко­то­ро­го вы­хо­дит эта диа­го­наль, равен 120°. Най­ди­те пло­щадь ромба, де­лен­ную на

114. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, ле­жа­щий на­про­тив этой диа­го­на­ли, равен 30°. Най­ди­те пло­щадь ромба.

115. Диа­го­наль AC па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 30° и 45°. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма. Ответ дайте в гра­ду­сах.

116. Бо­ко­вая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 34, а ос­но­ва­ние равно 60. Най­ди­те пло­щадь этого тре­уголь­ни­ка.

117. Пе­ри­метр квад­ра­та равен 40. Най­ди­те пло­щадь квад­ра­та.

118. Най­ди­те пло­щадь кру­го­во­го сек­то­ра, если длина огра­ни­чи­ва­ю­щей его дуги равна 6 π, а угол сек­то­ра равен 120°. В от­ве­те ука­жи­те пло­щадь, де­лен­ную на π.

119. Вы­со­та BH ромба ABCD делит его сто­ро­ну AD на от­рез­ки AH = 24 и HD = 2. Най­ди­те пло­щадь ромба.

120. 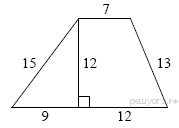Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

121. Най­ди­те пло­щадь пря­мо­уголь­ни­ка, если его пе­ри­метр равен 92, а от­но­ше­ние со­сед­них сто­рон равно 3:20.

122. Бо­ко­вая сто­ро­на тра­пе­ции равна 5, а один из при­ле­га­ю­щих к ней углов равен 30°. Най­ди­те пло­щадь тра­пе­ции, если её ос­но­ва­ния равны 3 и 9.

123. Пе­ри­метр ромба равен 24, а тан­генс од­но­го из углов равен . Най­ди­те пло­щадь ромба.

124. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, из ко­то­ро­го вы­хо­дит эта диа­го­наль, равен 30°. Най­ди­те пло­щадь ромба.

125. В тре­уголь­ни­ке ABC от­ре­зок DE — сред­няя линия. Пло­щадь тре­уголь­ни­ка CDE равна 97. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

126. На сто­ро­не BC пря­мо­уголь­ни­ка ABCD, у ко­то­ро­го AB = 24 и AD = 31, от­ме­че­на точка E так, что ∠ EAB = 45°. Най­ди­те ED.

127. Одна из сто­рон па­рал­ле­ло­грам­ма равна 12, дру­гая равна 5, а тан­генс од­но­го из углов равен . Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

128. В рав­но­бед­рен­ном тре­уголь­ни­ке бо­ко­вая сто­ро­на равна 10, ос­но­ва­ние — , а угол, ле­жа­щий на­про­тив ос­но­ва­ния, равен 120°. Най­ди­те пло­щадь тре­уголь­ни­ка, де­лен­ную на

129. В пря­мо­уголь­ном тре­уголь­ни­ке ги­по­те­ну­за равна 10, а один из ост­рых углов равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

130. Най­ди­те пло­щадь ромба, если его диа­го­на­ли равны 14 и 6.

131. Вы­со­та BH ромба ABCD делит его сто­ро­ну AD на от­рез­ки AH = 5 и HD = 8. Най­ди­те пло­щадь ромба.

132. Пе­ри­метр квад­ра­та равен 160. Най­ди­те пло­щадь квад­ра­та.

133. Най­ди­те пло­щадь квад­ра­та, опи­сан­но­го во­круг окруж­но­сти ра­ди­у­са 83.

134. Вы­со­та рав­но­бед­рен­ной тра­пе­ции, про­ведённая из вер­ши­ны C, делит ос­но­ва­ние AD на от­рез­ки дли­ной 1 и 5. Най­ди­те длину ос­но­ва­ния BC.

135. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, из ко­то­ро­го вы­хо­дит эта диа­го­наль, равен 60°. Най­ди­те пло­щадь ромба, де­лен­ную на

136. В пря­мо­уголь­ни­ке диа­го­наль равна 10, угол между ней и одной из сто­рон равен 30°, длина этой сто­ро­ны . Най­ди­те пло­щадь пря­мо­уголь­ни­ка, де­лен­ную на

137. Пе­ри­метр ромба равен 24, а синус од­но­го из углов равен . Най­ди­те пло­щадь ромба.

138. Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

139. В пря­мо­уголь­ни­ке одна сто­ро­на равна 10, пе­ри­метр равен 44. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.

140. Ос­но­ва­ния тра­пе­ции равны 10 и 11. Най­ди­те бóльший из от­рез­ков, на ко­то­рые делит сред­нюю линию этой тра­пе­ции одна из её диа­го­на­лей.

141. В рав­но­бед­рен­ном тре­уголь­ни­ке . Най­ди­те , если вы­со­та .

142. Пло­щадь па­рал­ле­ло­грам­ма равна 189. Точка 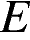— се­ре­ди­на сто­ро­ны . Най­ди­те пло­щадь тра­пе­ции .

 

143.

Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.

144. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 10, а угол, ле­жа­щий на­про­тив него, равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

145. Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

146. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.

147. В рав­но­бед­рен­ном тре­уголь­ни­ке бо­ко­вая сто­ро­на равна 10, ос­но­ва­ние — , а угол, ле­жа­щий на­про­тив ос­но­ва­ния, равен 150°. Най­ди­те пло­щадь тре­уголь­ни­ка.

148. Най­ди­те пло­щадь квад­ра­та, если его диа­го­наль равна 1.

149. В тре­уголь­ни­ке ABC от­ме­че­ны се­ре­ди­ны M и N сто­рон BC и AC со­от­вет­ствен­но. Пло­щадь тре­уголь­ни­ка CNM равна 2. Най­ди­те пло­щадь четырёхуголь­ни­ка ABMN.

150. Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

151. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см × 1 см от­ме­че­ны точки А, В и С. Най­ди­те рас­сто­я­ние от точки А до се­ре­ди­ны от­рез­ка ВС. Ответ вы­ра­зи­те в сан­ти­мет­рах.

152. Пло­щадь одной клет­ки равна 1. Най­ди­те пло­щадь фи­гу­ры, изоб­ражённой на ри­сун­ке.

153. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1×1 от­ме­че­ны точки A, B и C. Най­ди­те рас­сто­я­ние от точки A до се­ре­ди­ны от­рез­ка BC.

154. На ри­сун­ке изоб­ра­жен па­рал­ле­ло­грамм . Ис­поль­зуя ри­су­нок, най­ди­те .

155. Най­ди­те тан­генс угла AOB, изоб­ражённого на ри­сун­ке.

156. Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

157. На ри­сун­ке изоб­ра­жен ромб . Ис­поль­зуя ри­су­нок, най­ди­те .

158. Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.

159. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1см x 1см от­ме­че­ны точки А, В и С. Най­ди­те рас­сто­я­ние от точки А до пря­мой ВС. Ответ вы­ра­зи­те в сан­ти­мет­рах.

160. Най­ди­те тан­генс угла, изоб­ражённого на ри­сун­ке.

161. Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

162. Най­ди­те тан­генс угла тре­уголь­ни­ка , изоб­ражённого на ри­сун­ке.

163. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1см x 1см от­ме­че­ны точки А, В и С. Най­ди­те рас­сто­я­ние от точки А до се­ре­ди­ны от­рез­ка ВС. Ответ вы­ра­зи­те в сан­ти­мет­рах.

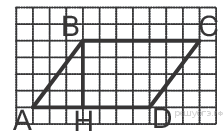
164.

На ри­сун­ке изоб­ражён пря­мо­уголь­ный тре­уголь­ник. Най­ди­те длину ме­ди­а­ны тре­уголь­ни­ка, про­ведённую из вер­ши­ны пря­мо­го угла.

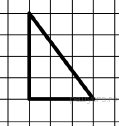
165. 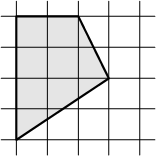Пло­щадь одной клет­ки равна 1. Най­ди­те пло­щадь за­кра­шен­ной фи­гу­ры.

166. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1x1 изоб­ра­же­на фи­гу­ра. Най­ди­те её пло­щадь.

167. Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.

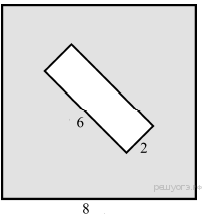
168. 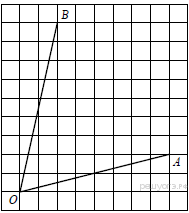Най­ди­те тан­генс угла AOB.

169. 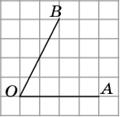Най­ди­те тан­генс угла AOB, изоб­ражённого на ри­сун­ке.

170. Най­ди­те тан­генс угла В тре­уголь­ни­ка ABC, изоб­ражённого на ри­сун­ке.

171. Най­ди­те тан­генс угла AOB.

172. На квад­рат­ной сетке изоб­ражён угол . Най­ди­те .

173. На ри­сун­ке изоб­ра­же­на тра­пе­ция . Ис­поль­зуя ри­су­нок, най­ди­те .

174. Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.

175. Пло­щадь одной клет­ки равна 1. Най­ди­те пло­щадь фи­гу­ры, изоб­ражённой на ри­сун­ке.

176. 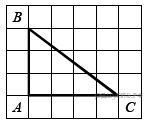Най­ди­те тан­генс угла тре­уголь­ни­ка , изоб­ражённого на ри­сун­ке.

177.

Най­ди­те синус остро­го угла тра­пе­ции, изоб­ражённой на ри­сун­ке.

178. На ри­сун­ке изоб­ра­же­на тра­пе­ция . Ис­поль­зуя ри­су­нок, най­ди­те .

179. На ри­сун­ке изоб­ра­жен ромб . Ис­поль­зуя ри­су­нок, най­ди­те .

180. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1см × 1см изоб­ра­же­на тра­пе­ция. Най­ди­те её пло­щадь. Ответ дайте в квад­рат­ных сан­ти­мет­рах.

181. Най­ди­те тан­генс угла тре­уголь­ни­ка , изоб­ражённого на ри­сун­ке.

182. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1см × 1см изоб­ражён па­рал­ле­ло­грамм. Най­ди­те длину его боль­шей вы­со­ты. Ответ дайте в сан­ти­мет­рах.

183. 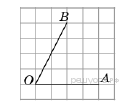Най­ди­те тан­генс угла AOB, изоб­ра­жен­но­го на ри­сун­ке.