Любая система регулирования может быть представлена рядом элементов, выполняющих свои функции. В представленном курсовом проекте рассмотрена непрерывная система регулирования, состоящая из объекта регулирования, автоматического регулятора, датчика и исполнительного механизма.
Устойчивостью САР называется способность системы возвращаться в исходное состояние, из которого она была выведена под действием внешних возмущающих факторов, после прекращения действия этих факторов.
Устойчивость является необходимым условием нормального функционирования САР. Наличие устойчивости свидетельствует о том, что переходный процесс, вызванный действием внешнего воздействия или существованием ненулевых начальных условий, является затухающим.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Таблица 1. Характеристики звеньев системы
| Объекты | Статическая характеристика | Передаточная функция |
| Регулятор | 
| 
|
| Датчик |
| 
|
| Исполнительный механизм | 
|
|
| Объект регулирования |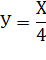 
| 
|
Для нормального функционирования автоматической системы управления необходимо провести расчёт её параметров на устойчивость.
В соответствии с заданием курсового проекта имеем статическую характеристику объекта регулирования, которая описывается уравнением
Для построения статической характеристики объекта регулирования необходимо давать текущие значения для Х Вх.Здесь достаточно определить две точки, чтобы построить характеристику. Положим X 0 =0 и получим Y0 = 0, положим X0 =1 и получим Y0 = 4. По этим двум точкам построена прямая, показана на рис 1.
чертеж
|
|
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Для определения статической характеристики цепи обратной связи выбираются статические характеристики датчика, регулятора и исполнительного механизма.
Статическая характеристика датчика описывается уравнением:
Эта характеристика является нелинейной. Для дальнейшего его применения аппроксимируем её прямой линией, которая показана на рисунке2.
чертёж
Рис 2.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Эта характеристика такжеотносится к классу нелинейных. Для её достаточно взять три точки.Статическая характеристика регулятора приведена на рис.3.
чертеж
Рис 3.
Статическая характеристика исполнительного механизма описывается уравнением.
Для построения этой линейной статической характеристики достаточно задать Хи.м. три значения.
Эти цифры дают основание провести прямую, которая отображается на рис.5.
чертёж
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Рис 4.
Чертеж дрим
Рис 5.
· Для определения общей статической характеристики цепи обратной связи (ДРИМ) изобразим статические характеристики этих звеньев на общей плоскости. В первом квадрате находится статическая характеристика датчика, во втором – регулятора, в третьем – исполнительного механизма (рис.4). Для определения результирующей статической характеристики разбиваем ось 
на равные отрезки 0 -1, 1 -2, 2 -3, и т.д. проводим перпендикуляры до пересечения с линейной статической характеристикой датчика. Получаем точки 
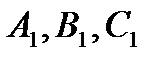и т.д. Из этих точек проводим горизонтали до пересечения с линейной статической характеристикой регулятора в точках 
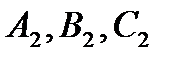и т.д. Из этих точек опускаем перпендикуляры. Горизонтальное положение оси 
меняется на вертикальное. Из новых точек проводятся горизонтали до пересечения с соответствующими перпендикулярами в точках A, B, C и т.д. Соединяя эти точки, получим результирующую статистическую характеристику обратной связи – ДРИМ (рис. 5)
|
|
· Для определения взаимосвязи между статическими характеристиками объекта и ДРИМ изобразим их в одной системе координат. В результате эти две статические характеристики пересекутся в точке А (рис.6). Эта точка называется рабочей. Угол пересечения этих двух статических характеристик равен 84°.
· Из теории автоматического регулирования известно: при пересечении двух статических характеристик под углом 60…90º система характеризуется хорошей устойчивостью.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
· Для расчета динамического коэффициента регулирования обратимся к рис.6. На этом рисунке по одной из характеристик определяется возможный диапазон изменений входного параметра. Фиксируются две точки этого диапазона, далее эти две точки переносятся на вторую статическую характеристику, и с помощью этой характеристики определяется диапазон изменения входного параметра. В результате по статистической характеристике ДРИМ определим 
, по статической характеристике объекта получим 
. Подставим эти значения в выражение 
(при D=1 система имеет оптимальную передачу сигнала в замкнутом контуре, при D>1 в цепь обратной связи следует включить ослабитель сигнала; при D<1 следует включить усилительный элемент).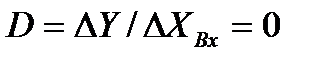 
|
|
Так как нам нужен динамический коэффициент, равный единице, в цепь обратной связи включен усилительный элемент с коэффициентом передачи К=20. Включение усилительного звена в цепь обратной связи показано на рис.7.
| --- |
| ОР |
| ОС |
рис.7
• Для определения аналитического выражения работы регулирующей системы осуществим преобразования статических характеристик датчика, регулятора и исполнительного механизма.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Уравнение для объекта регулирования:
Уравнение для датчика:
Уравнение для регулятора:
Уравнение для исполнительного механизма:
Из структурной схемы системы следует, что 
; 
Подставим уравнение датчика в уравнение для регулятора. Результирующее уравнение подставим в уравнение для исполнительного механизма:
= 
= 
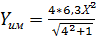= 6,1 
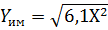
В результате получено выражение: 2,5Х
Это выражение является статической характеристикой цепи обратной связи, полученной аналитическим способом. Оно также описывает статическую характеристику цепи обратной связи, полученную ранее графическим способом.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Поскольку статические характеристики представляются прямыми линиями, то необходимо найти точку пересечения двух прямых линий. Эти линии задаются уравнениями.
Обозначим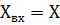 
и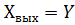 
, в результате получим: 
Решим систему уравнений. Определим координаты рабочей точки:
X=0; Y=0 A (0; 0)
А теперь перейдем к расчету динамических параметров системы.
Для определения передаточной функции всей системы необходимо по справочным данным выбрать передаточные функции датчика, регулятора и исполнительного механизма.
Передаточная функция объекта регулирования дана в задании и определяется выражением:
По справочным данным выбираем передаточные функции.
Передаточная функция датчика:
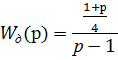
Передаточная функция регулятора:
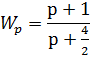
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Передаточная функция исполнительного механизма:
Для определения передаточной функции обратной связи (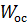
) необходимо воспользоваться формулой:
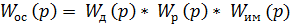
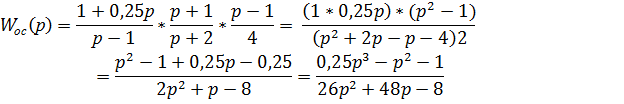
Дляопределения передаточной функции системы воспользуемся выражением:
Подставим сюда все составляющие передаточные функции и преобразуем результирующие выражение:
= 
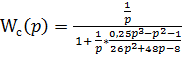Передаточная функция системы описывается выражением:
Для нахождения временной функции переходного процесса необходимо упростить это выражение. Для дальнейшего исследования передаточная функция будет иметь вид.
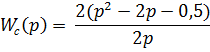
Для определения переходной функции представим общее выражение в виде двух слагаемых. Эти слагаемые можно получить, если определить корни характеристического уравнения.
где p1 и p2 – значения корней характеристического уравнения.
Для определения корней характеристического уравнения приравняем к нулю знаменатель:
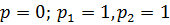
Подставим значения характеристического уравнения p1 и p2 в выражение
и таким образом определим коэффициенты Aи B:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
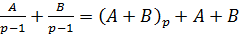
A =1
B =1
Для определения функции времени необходимо воспользоваться обратным преобразованием Лапласа:
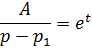
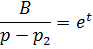
Далее определяем переходную функцию системы, которая определяется выражением:
Преобразуем это выражение к виду:
Подставив выражения А и В, получим:
Сгруппируем слагаемые в квадратных скобках таким образом, чтобы сформировать уравнение Эйлера. В результате получим:
Две гармонические функции можно заменить одной, если определить модуль и фазу результирующего колебания.
Определим модуль:
а=1;b=1;
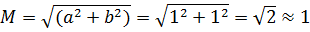
В результате получим выражение:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
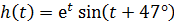
Переведём величину угла в градусах в радианы и получим:
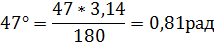
Рис.8 График переходной функции.
Определение основных параметров системы следует производить с учетом построенного графика h(t)
Приступим к определению амплитудно-частотных характеристик звеньев и системы в целом. Для определения частотной характеристики объекта регулирования произведем замену в передаточной функции объекта.
p=iw
, сделав замену p=iw, получим частотную характеристику объекта регулирования.
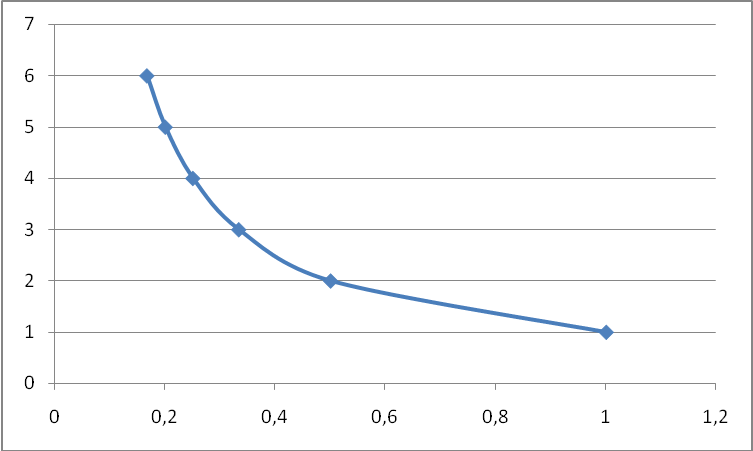
Рис.9 Частотная характеристика объекта регулирования.
Определим частотную функцию датчика: 
Для выделения действительного и мнимого значений умножаем числитель и знаменатель на комплексно-сопряженное значение знаменателя:
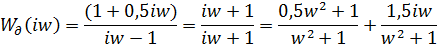
В результате получим действительную и мнимые части. Далее определим модуль, полагая что:
Где 
. Если вэто выражение подставить текущие значения w, то получим 
Далее строим, график (рис.10), зная, что:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
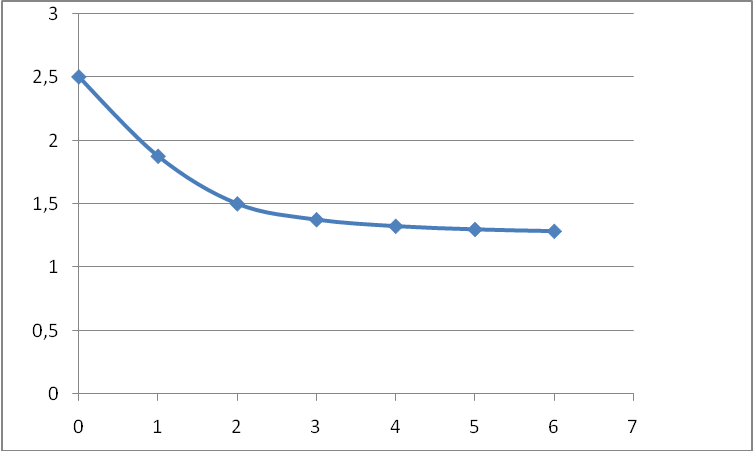
Рис.10 Амплитудно-частотная характеристика.
Определим спектральную характеристику исполнительного механизма:
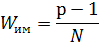
Произведем замену в передаточной функции регулятора:
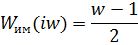
Здесь для построения спектральной характеристики исполнительного механизма даются текущие значения w и определяется 
(рис. 11)
Рисунок
Определим спектральную характеристику регулятора.
Передаточная функция имеет вид:
Примем p = iw и получим
Для выделения действительного и мнимого значений умножаем числитель и знаменатель на комплексно-сопряженное значение знаменателя:
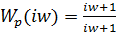
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
= 
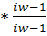Выделим действительную и мнимую части. Определим модуль, полагая что:
= 
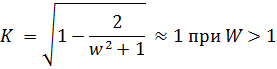
Далее строим график (рис. 12) с учетом выражения:
РИСУНОК
Определим частотную характеристику обратной связи ДРИМ. Имеем передаточную функцию:
Для определения спектральной характеристики цепи обратной связи – ДРИМ воспользуемся выражением:
Здесь необходимо для каждого текущего значения w определить ординаты в частотных характеристиках датчика, регулятора и исполнительного механизма и перемножить их. В результате этого действия получим следующие значения:
По этим координатам строится частотный спектр цепи обратной связи (рис. 13)
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Частотную характеристику всей системы можно записать выражением: