Курсовая работа
По дисциплине: «Теоретическая механика»
«Исследование движения механической системы с использованием общих теорем и принципов динамики»
А-261(2)
Выполнил Проверил
Студент: Ларионов Д.С. Преподаватель: Каиров Т.В.
Дата: ____________ Дата: _____________
Подпись: _________ Подпись: __________
Оценка: ___________
Мурманск
 Содержание
Содержание
1. Исследование движения механической системы с использованием общего уравнения динамики …………………………………………2
2. Исследование движения механической системы с использованием общего уравнения динамики в обобщенных координатах (уравнение Лагранжа второго рода)………………………………………………..7
3. Список использованной литературы…………………………………10
Исследование движения механической системы с использованием общего уравнения динамики
 |
Исходные данные
Д3
| т1, кг | т2, кг | т3, кг | R1, м | R2, м | r2, м |  ,
м ,
м
| Р, Н | М,

| Мс,

|
| 250 | 150 | 400 | 0,4 | 0,3 | 0,15 | 0,2 | 15000 | 6000 | 500 |
 Применим в ходе анализа движения механизма общее уравнение динамики.
Применим в ходе анализа движения механизма общее уравнение динамики.
1.1 Зададим направления ускорений ( ,
,  ,
,  ) звеньев механизма. Предположим, что направления этих ускорений совпадают с положительным направлением координат
) звеньев механизма. Предположим, что направления этих ускорений совпадают с положительным направлением координат  ,
,  ,, определяющих положение этих звеньев. Приложим к телам системы силовые факторы инерции. Силы инерции звеньев 1 и 2, вращающихся вокруг осей
,, определяющих положение этих звеньев. Приложим к телам системы силовые факторы инерции. Силы инерции звеньев 1 и 2, вращающихся вокруг осей  и
и  , соответственно приводятся к моментам сил инерции
, соответственно приводятся к моментам сил инерции  и
и  направленным противоположно соответствующим ускорениям
направленным противоположно соответствующим ускорениям  и
и  , величины которых равны:
, величины которых равны:


 Сила инерции груза 3, движущегося поступательно с ускорением
Сила инерции груза 3, движущегося поступательно с ускорением  , направлена противоположно ускорению
, направлена противоположно ускорению  и численно равна
и численно равна

Учитывая, что взаимосвязь между ускорениями:

выражения (1.1) и (1.2) примут вид:


1.2Зададим механической системе возможное перемещение ( ,
,  ,
,  ) в направлении положительного отсчета соответствующих координат и составим общее уравнение динамики для этой системы, приравняв к нулю сумму элементарных работ всех внешних (заданных) сил и сил инерции материальных точек системы на этом возможном перемещении:
) в направлении положительного отсчета соответствующих координат и составим общее уравнение динамики для этой системы, приравняв к нулю сумму элементарных работ всех внешних (заданных) сил и сил инерции материальных точек системы на этом возможном перемещении:


В нашем случае на механическую систему действуют силы тяжести  ,
,  ,
,  , вращающий момент
, вращающий момент  , момент сопротивления вращению
, момент сопротивления вращению 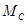 , силы реакции в опорах
, силы реакции в опорах  ,
,  ,
,  ,
,  , и силы инерции
, и силы инерции 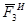 ,
,  ,
,  . Поскольку на систему наложены идеальные связи (шарниры без трения
. Поскольку на систему наложены идеальные связи (шарниры без трения  и
и 
 гибкая нерастяжимая нить, а также существует внутренняя связь между звеньями 1 и 2, которую можно представить либо как зубчатое зацепление без трения, либо как фрикционное зацепление без проскальзывания), то по определению элементарная работа сил реакций идеальной связи равна нулю и не входит в (1.4). Заметим сразу же, что равны нулю и не входят в (1.4) элементарные работы сил
гибкая нерастяжимая нить, а также существует внутренняя связь между звеньями 1 и 2, которую можно представить либо как зубчатое зацепление без трения, либо как фрикционное зацепление без проскальзывания), то по определению элементарная работа сил реакций идеальной связи равна нулю и не входит в (1.4). Заметим сразу же, что равны нулю и не входят в (1.4) элементарные работы сил  ,
,  ,
,  ,
,  ,
,  ,
, 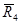 , так как эти силы приложены к неподвижным точкам. Знак каждой работы устанавливается по общему правилу: если направление силового фактора (силы или момента) совпадает с направлением соответствующего ему перемещения (линейного или углового), то работа считается положительной, в противном случае работа силового фактора отрицательна.
, так как эти силы приложены к неподвижным точкам. Знак каждой работы устанавливается по общему правилу: если направление силового фактора (силы или момента) совпадает с направлением соответствующего ему перемещения (линейного или углового), то работа считается положительной, в противном случае работа силового фактора отрицательна.
Итак, общее уравнение динамики для нашей механической системы имеет вид:
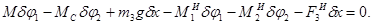
Приведем зависимости между координатами звеньев:


Так как на механическую систему наложены стационарные и голономные связи, то записать зависимости между возможными перемещениями звеньев можно аналогично (1.5):


С учетом (1.6) выражение (1.5) примет вид:

После сокращения на 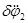 имеем
имеем


 Подставив в (1.7) вместо
Подставив в (1.7) вместо 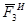 ,
,  ,
,  их выражения из (1.3), получим
их выражения из (1.3), получим

откуда


Подставив в (1.8) исходные данные, находим
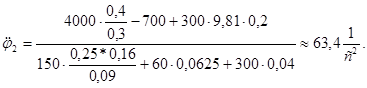
Определив угловое ускорение  звена 2, найдем закон его движения:
звена 2, найдем закон его движения:

Проинтегрируем это равенство, учитывая, что для начала движения  20 = 0 и
20 = 0 и  20 = 0:
20 = 0:

Откуда  .
.
Учитывая, что  и выполнив аналогичные преобразования, получим
и выполнив аналогичные преобразования, получим

 1.3. Исследовательская часть
1.3. Исследовательская часть
Для определения натяжения нити, на которой подвешен груз 3, и окружного усилия в точке касания звеньев 1 и 2 составим общее уравнение динамики для звена 1 и отдельно для груза 3. При этом искомые усилия становятся внешними силами по отношению к этим телам. Для звена 2 общее уравнение динамики примет вид

Откуда

Для груза 3 общее уравнение динамики примет вид

откуда, учитывая, что 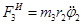 , имеем
, имеем

2.Исследование движения механической системы с использованием общего уравнения динамики в обобщенных координатах (уравнение Лагранжа второго рода)
Исходные данные
Д4
 кг
кг
|  кг
кг
|  кг
кг
| 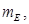 кг
кг
|  м
м
|  м
м
|  м
м
|  м
м
| 
| f | S, м |
| 0,5 | 0,3 | 0,4 | 0,2 | 60◦ | 0,11 |
 |
 Рассмотрим движение неизменяемой системы с идеальными связями, движущимися под воздействием внешних сил:
Рассмотрим движение неизменяемой системы с идеальными связями, движущимися под воздействием внешних сил:
· тяжести 

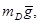

· трения скольжения 
Реакции идеальных связей не учитываем, так как их элементарная работа равна 0.
Применим для анализа движения рассматриваемой механической системы на заданном перемещении S уравнение Лагранжа второго рода:
 (2.1)
(2.1)
Где –Т- кинетическая энергия системы за время движения;
q- обобщенная координата системы (q=x);
 - обобщенная скорость системы (
- обобщенная скорость системы ( =
=  =
=  );
);
 - обобщенная сила системы, соответствующая обобщенной координате. С учетом принятых обозначений (2.1) примет вид:
- обобщенная сила системы, соответствующая обобщенной координате. С учетом принятых обозначений (2.1) примет вид:
 (2.2)
(2.2)
Кинетическая энергия механической системы была найдена в РГЗ №1:
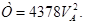 (2.3)
(2.3)
Найдем сумму элементарных работ всех действующих на систему внешних сил бесконечно малом перемещении тела А

Сумму элементарных работ всех внешних сил найдем по формуле:
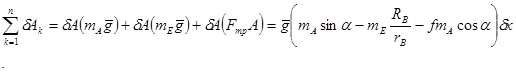 (2.4)
(2.4)
По определению, обобщенная сила, соответствующая обобщенной координате х, равна:
 (2.5)
(2.5)
Вычислим производные уравнения (2.2):


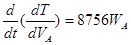 (2.6)
(2.6)
Подставляя (2.5) и (2.6) в (2.2) имеем:

Определим скорость тела А:

Умножив последнее равенство на  , получим:
, получим:
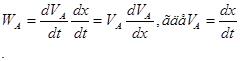
 Выше было указано, что
Выше было указано, что
 , поэтому:
, поэтому:

Проинтегрировав данное равенство и учитывая, что x=S, получим:

откуда:

Список использованной литературы:
 |
1. Айзерман Т. Б. и др. Руководство к решению задач по теоретической механике. – М.: Высш. шк., 1985. – 367 с.
2. Бать И. и др. Теоретическая механика в примерах и задачах. – М.: Высш. шк., 1990. – 631 с.
3. Тарг С.М. Краткий курс теоретической механики: Учеб. Для втузов. – 10-е изд., перераб. и доп. – М.: Высш. шк., 1986. – 416 с.