Слайд 4.
4.2. ЦИФРОВОЙ ДИФФЕРЕНЦИАЛЬНЫЙ АНАЛИЗАТОР
Один из методов разложения отрезка в растр состоит в решении дифференциального уравнения, описывающего этот процесс. Для прямой линии имеем
| |||
| |||
Решение представляется в виде
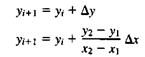
где x1, y1, x2, y2 — концы разлагаемого отрезка yi — начальное значение для очередного шага вдоль отрезка. Фактически уравнение (4.1) представляет собой рекуррентное соотношение для последовательных значений Y вдоль нужного отрезка. Этот метод, используемый для разложения в растр отрезков, называется цифровым дифференциальным анализатором (ЦДА). В простом ЦДА либо dх, либо dУ (большее из приращений) выбирается в качестве единицы растра. Ниже приводится простой алгоритм.

Рис. 4.3 – Отрезок прямой.
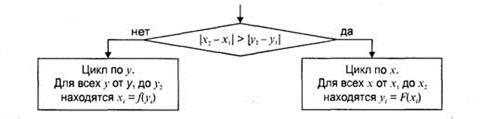
Рис. 4.4 – Общая схема алгоритма вывода отрезка прямой линии
Положительные черты прямого вычисления координат.
1. Простота, ясность построения алгоритма.
2. Возможность работы с нецелыми значениями координат отрезка.
Недостатки.
1. Малая скорость из-за использования операций с плавающей точкой или целочисленных операций умножения и деления.
2. При вычислении координат добавлением приращений может накапливаться ошибка вычисления координат.
Последнюю разновидность прямого вычисления координат, рассмотренную здесь, можно было бы назвать "инкрементной". Но такое название получили алгоритмы другого типа.
4.3. АЛГОРИТМ БРЕЗЕНХЕМА
Брезенхэм предложил подход, позволяющий разрабатывать так называемые инкрементные алгоритмы растеризации. Основной целью при разработке таких алгоритмов было построение циклов вычисления координат на основе только целочисленных операций сложения/вычитания без использования умножения и деления для увеличения быстродействия вычислений каждого пикселя по сравнению с прямым способом. Инкрементные алгоритмы выполняются как последовательное вычисление координат соседних пикселов путем добавления приращений координат. Приращения рассчитываются на основе анализа функции погрешности.
Алгоритм выбирает оптимальные растровые координаты для представления отрезка. В процессе работы одна из координат — либо x, либо у (в зависимости от углового коэффициента) — изменяется на единицу. Изменение другой координаты (либо на нуль, либо на единицу) зависит от расстояния между действительным положением отрезка и ближайшими координатами сетки. Такое расстояние мы назовем ошибкой.
Слайд 8. Алгоритм построен так, что требуется проверять лишь знак этой ошибки. На рис. 4.5 это иллюстрируется для отрезка в первом октанте, т. е. для отрезка с угловым коэффициентом, лежащим в диапазоне от нуля до единицы. Из рисунка можно заметить, что если угловой коэффициент отрезка из точки (0, 0) больше чем 1/2, то его пересечение с прямой х = 1 будет расположено ближе к прямой у = 1, чем к прямой у = 0. Следовательно, точка растра (1, 1) лучше аппроксимирует ход отрезка, чем точка (1, 0). Если угловой коэффициент меньше 1/2, то верно обратное. Для углового коэффициента, равного 1/2, нет какого-либо предпочтительного выбора. В данном случае алгоритм выбирает точку (1, 1).

Рис.4.5 – Основная идея алгоритма Брезенхейма

Рисунок 4.6 – Изображение отрезка в растре при его построении методом Брезенхема (а) и график ошибки (б)
Не все отрезки проходят через точки растра. Подобная ситуация иллюстрируется рис. 4.6, где отрезок с тангенсом угла наклона 3/8 сначала проходит через точку растра (0, 0) и последовательно пересекает три пиксела. Также иллюстрируется вычисление ошибки при представлении отрезка дискретными пикселами. Так как желательно проверять только знак ошибки, то она первоначально устанавливается равной —1/2. Таким образом, если угловой коэффициент отрезка больше или равен 1/2, то величина ошибки в следующей точке растра с координатами (1,0) может быть вычислена как
е = е + m
где m — угловой коэффициент. В нашем случае при начальном значении ошибки е0 = -1/2
е1 = -1/2+ 3/8 = -1/8
Так как е отрицательно, отрезок пройдет ниже середины пиксела. Следовательно, пиксел на том же самом горизонтальном уровне лучше аппроксимирует положение отрезка, поэтому у не увеличивается. Аналогично вычисляем ошибку
е2 = -1/8 + 3/8 = 1/4
в следующей точке растра (2, 0). Теперь е положительно, а значит, отрезок пройдет выше средней точки. Растровый элемент (2, 1) со следующей по величине координатой у лучше аппроксимирует положение отрезка. Следовательно, у увеличивается на единицу. Прежде чем рассматривать следующий пиксел, необходимо откорректировать ошибку вычитанием из нее единицы. Имеем
е2’ = 1/4- 1 = -3/4
Заметим, что пересечение вертикальной прямой х = 2 с заданным отрезком лежит на 1/4 ниже прямой y = 1. Если же перенести отрезок 1/2 вниз, мы получим как раз величину -3/4. Продолжение вычислений для следующего пиксела дает
e3 = - 3/4 + 3/8 = - 3/8
Так как e отрицательно, то у не увеличивается. Из всего сказанного следует, что ошибка — это интервал, отсекаемый по оси у рассматриваемым отрезком в каждом растровом элементе (относительно —1/2).
Модифицированный алгоритм Брезенхема
Основная идея алгоритма состоит в том, чтобы для ребер многоугольника устанавливать яркость пиксела пропорционально площади пиксела, попавшей внутрь многоугольника.
На рис. приведена иллюстрация построения ребра многоугольника с тангенсом угла наклона 11/21.
На рис. а) показан результат генерации многоугольника с использованием ранее рассмотренного алгоритма Брезенхема при двухуровневом изображении (пиксел или закрашен или не закрашен).
На рис. б) показан результат генерации многоугольника с вычислением интесивности пикселов, через которые проходит ребро многоугольника. Интенсивность вычисляется пропорциональной площади части пиксела, попавшей внутрь многоугольника.
На рис. в) показан результат генерации многоугольника с вычислением интесивности пиксела, через который проходит ребро многоугольника в соответствии с модифицированным алгоритмом Брезенхема.
Как видно из рис. при построении ребра многоугольника с тангенсом угла наклона t (0 £ t £ 1) могут захватываться либо один пиксел (пикселы (0,0), (2,1), (4,2), (6,8)) либо два пиксела (пикселы (1,0) и (1,1), (3,1) и (3,2), (5,2) и (5,3)). Если захватывается один пиксел, то часть его площади, попавшая внутрь многоугольника, равна dy + t/2 (рис. a).
Если же захватывается два пиксела, то часть площади нижнего пиксела, попавшая внутрь многоугольника равна 1 - [((1 - dy)2)/ 2t], а верхнего - [((dy - 1 + 2)2)/ 2t] (см. рис. б). Суммарная площадь частей для двух пикселов, попавшая внутрь многоугольника, равна dy + t/2.
Если теперь в исходном алгоритме Брезенхема (см. 2) заменить отклонение E на E' = E + (1-t), то 0 £ E' £ 1) и значение E' будет давать значение той части площади пиксела, которая находится внутри многоугольника.
Выполняя преобразование над значением отклонения для первого шага (см. 2) получим, что начальное значение станет равным 1/2. Максимальное значение отклонения E'max, при превышении которого производится увеличение Y-координаты занесения пикселов, станет равным (1 - t).

Рис. 5: Устранение ступенчатости ребер многоугольника
а) генерация ребер без устранения ступенчатости;
б) точное вычисление интенсивности пикселов границы;
в) формирование пикселов границы по модифицированному методу Брезенхема.

Рис. 6: Устранение ступенчатости за счет учета площади пикселов, пересекаемых ребром многоугольника
Для того, чтобы оперировать не дробной частью максимальной интенсивности, а непосредственно ее значениями достаточно домножить на полное число уровней интенсивности I тангенс угла наклона (t), начальное (E') и максимальное (E'max) значения отклонения.

