Наконец-то длительные каникулы подошли к концу, и я рад приветствовать ценителей интегрального исчисления на новом уроке! Сегодня мы зайдём немножко в дебри темы, которые освещены далеко не во всех учебниках по математическому анализу. И это большое упущение, поскольку задачи на вычисление поверхностных интегралов встречаются даже у студентов-заочников. Что тут сказать… – Пробелы есть, пробелы нужно закрывать!
Итак, что же такое поверхностный интеграл? Из самого названия следует, что здесь речь идёт об объединении (интегрировании) некоторой величины по поверхности. Представьте лесную полянку с муравьями…, где-то их больше, где-то меньше, и цель поверхностного интегрирования состоит в том, чтобы вычислить суммарную «муравьиную массу» по поверхности поляны.
И этот «детский» пример не так далёк от сути – поверхностные интегралы получили широчайшее распространение в физике, где часто возникает надобность подсчитать ту или иную физическую величину по поверхности. Но коль скоро сайт посвящён математике, то в рамках данного урока я не буду рассматривать все эти приложения, а остановлюсь на технической стороне вопроса – чтобы у вас не возникало трудностей именно с вычислением поверхностных интегралов.
Начнём с условностей и обозначений.
Поверхности. В практических задачах, как правило, встречаются «обычные», а также кусочно-гладкие поверхности, состоящие из «кусков» плоскостей, цилиндров, параболоидов и иже с ними. Далее по умолчанию будем подразумевать только «хорошие» ограниченные (грубо говоря, не бесконечные) поверхности, позволяющие беспроблемно интегрировать. Система координат по дефолту прямоугольная декартова 
– тоже удобная и хорошая.
Поверхность обычно обозначают буквой 
или 
. Последний вариант хоть и распространён, но не слишком хорош, так как ассоциируется с площадью; «омега» сложнА для написания, а посему поверхность условимся обозначать буквой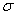 
.
Поверхностный интеграл по поверхности 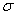обозначают удвоенным значком интеграла:
И здесь сразу возникает вопрос: поверхность – она же в пространстве, так почему интеграла только два? Дело в том, что пространственная поверхность – это объект двумерный. Простейшее доказательство проведём с помощью полюбившегося наглядного пособия =) Расстелите на полу одеяло и задайте на нём, например, декартову систему 
. Сколько координат нужно указать, чтобы определить любую точку одеяла? Две. Теперь поднимите одеяло и произвольно изогните его в пространстве.
Ещё более наглядный пример – наш земной шар эллипсоид. Любая точка его поверхности однозначно определяется двумя координатами (широтой и долготой).
Кстати, если поверхность 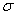ограничена, замкнута и лежит в плоскости , то представляет собой не что иное, как старый-знакомый двойной интеграл.
Ну а с другой точки зрения, поверхностный интеграл – это пространственный аналог криволинейного интеграла, и если у вас после этих фраз отлегло от сердца, то можете смело читать дальше =)
…правильно догадываетесь – поверхностные интегралы тоже бывают первого рода и второго рода.