Оглавление
| Оглавление | |
| Введение. | |
| Расчет допуска резисторов делителя напряжения на основе статистического анализа | |
| Листинг. | |
| Список используемой литературы |
Введение
Среди бурно развивающихся систем компьютерной математики, в первую очередь ориентированных на численные расчеты, особо выделяется матричная математическая система MATLAB.
MATLAB — это высокоуровневый язык и интерактивная среда для программирования, численных расчетов и визуализации результатов. С помощью MATLAB можно анализировать данные, разрабатывать алгоритмы, создавать модели и приложения.
Из-за большого числа поставляемых с системой пакетов расширения MATLAB является и самой большой из СКМ, ориентированных на персональные компьютеры, а также для устройств под управлением ОС Android. Эффективность MATLAB обусловлена, прежде всего, ее ориентацией на матричные вычисления, удачно реализованы средства работы с многомерными массивами, большими и разреженными матрицами и многими типами данных. Это мощная операционная среда для выполнения огромного числа математических и научно технических расчетов и вычислений, создания пользователями своих пакетов расширения и библиотек, процедур и функций. Новые версии системы имеют встроенный компилятор и позволяют создавать исполняемые файлы.
Система фактически стала мировым стандартом в области современного математического и научно технического программного обеспечения.
Расчет допуска резисторов делителя напряжения на основе статистического анализа
Целю работы является подбор резисторов по их допуску δR, для получения резистивного делителя напряжения на 2 с задаными точностными характеристиками. R1=470 Ом, R2=470 Ом. Допускается, что при нормальном законе распределения сопротивления резисторво выходное напряжение U2 отклонялось не более чем на δU=0.2% от заданного значения с вероятностью W.Напряжение на выходе делителя U1 = 10В, с допуском δЕ =0.1%. Требуемая вероятность нахождения напряжения в допуске 90%.
 | |||||||
 | |||||||
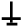 | |||||||
 |
Рисунок 1- схема делителя напряжения
Первый этап.
Нам необходимо сгенерировать вектор сопротивлений для резистора R1. Для этого используем функцию: rand. Данная функция формирует вектор со случайными значениями, распределенными по нормальному закону с математическим ожиданием равным нулю и G1.
Исходное распределение должно быть преобразованно так, чтобы математическое ожидание было равно номиналу резистора, а величина 3G – соответствует допуску резистора.
Для резистора с номиналом R 470 Ом. и допуском δR 10% выражение будет выглядеть следующим образом: R1=(47/3)* rand(1,1000)+470.
Второй этап.
Расчитываем напряжение на входе делителя с учетом случайного распределения сопротивлений резисторов по следующей формуле: U2=(U1.*R2)./(R1+R2).
Третий этап.
Необходимо отценить вероятность того, что при заданном допуске резисторов δR будут выполняться условия указанные в цели работ.
Для этого сформируем вспомогательный вектор, содержажий сортированные значения выходного напряжения U2S=sort(U2) и преобразуем гисторамму в переменную W=hist(U2,1000). Здесь второй параметр функции hist выбран совпадающим с общим числом испытаний, что обеспечивает точное соответствие между заданными векторе W и U2S.Найдем уровень напряжения соответствующий минимально допустимому уровню напряжения U2min=U2nom*(1-dU/100).
Найдем это значение в массиве M=find(U2S>U2min).
Для задания границ достаточно одного числа, в связи с чем, усечем вектор M=M(1).
Для допустимого отклонения выходного напряжения 0.2% нижняя граница напряжения определяется U2min=U2nom*(1-dU/100).
Поиск значения в массиве производится следующим образом M=find(U2S>U2min). Функция find возвращает номера всех элементов, однако, для задания границ достаточно одного числа, поэтому усечем вектор: М=М(1).
Для допустимого отклонения выходного напряжения δU равного 0,2% верхняя граница напряжения определяется U2max=U2nom*(1+dU/100).
Повторим поиск значения в массиве производится следующим образом N=find(U2S>U2max).
Вероятность попадания в заданный диапазон по напряжению определяется как сумма значений гистограммы в найденом диапазоне от М до N отнесенная к общему числу испытанмй. S=sum (W(M:N)/1000.
Четвертый этап.
На четвертом этапе проведем подбор допусков у резисторов таким образом, что бы выполнить условия цели работы (S>P). Для этого следует использовать цикл While.
Листинг.
U=10; %Напряжение на входе делителя
R=470; % Сопротивления резисторов R1 и R2
P=0.90; %Требуемая вероятность нахождения напряжения допуске
dE=0.1 %Отклонение входного напряжения
dU=0.2 %Допустимое отклонение входного напряжения
dR=10 %Допуск резисторов
%первый этап
R1=(R*dR/300)*randn(1,1000)+R; %Вектор сопротивлений для R1
hist(R1);figure(1); %Гистограмма R1
R2=(R*dR/300)*randn(1,1000)+R; %Вектор сопротивлений для R2
hist(R2);figure(2); %Гистограмма R2
U1=(U*dE/300)*randn(1,1000)+U; %Вектор напряжений U1
%второй этап
U2=(U1.*R2)./(R1+R2); %Расчет напряжения нв выходе
%третий этап
U2S=sort(U2);%Формирование вспомогательного вектора
U2nom=(U*R2)/(R1+R2); %вычисление вектора значений выходного напряжения
W=hist(U2,1000); % Преобразование гистограммы в переменную W
U2min=U2nom*(1-dU/100););%Вычисление нижней граници диапазона допустимых значений
M=find(U2S>U2min);% Поиск значений не превышающих минимальное допустимое значение
M=M(1);% Первое значение на нижней границе допустимого диапазона
U2max=U2nom*(1+dU/100); %Верхняя граница напряжения
N=find(U2S>U2max);%Поиск значений превышающих диапазона допустимых значений
N=N(1););% Первое значение на верхней границе допустимого диапазона
S=sum(W(M:N))/1000;%Вероятность попадания значения в заданный диапазон
%четвертый этап
while S>P
R1=(R*dR/300)*randn(1,1000)+R
R2=(R*dR/300)*randn(1,1000)+R
U1A=(U1*dE/300)*randn(1,1000)+U1
U2=(U1A.*R2)./(R1+R2);
U2nom=U1*R2/(R1+R2);
U2S=sort(U2);
U2min=U2nom*(1-dU/100);
M=find(U2S>U2min);
M=M(1);
U2max=5*(1+dU/100);
N=find(U2S>U2max);
N=N(1);%
S=sum(W(M:N))/1000;
dR=dR-0.2;
end;
disp ('конечный результат'), dr
Список используемой литературы:
1. Юдин А.В., Научно технические расчеты на ПЭВМ [Учебное пособие] / А.В. Юдин, С.Э. Седлецкая\\ РГАГУ им. П.А. Соловьева,-Рыбинск, 2011 г.
2. Применение програмного пакета «Матричная лаборатория» к решению задач теоретической электротехники: Учебное пособие в 2 ч./ Клюковкин В.Р., Камакин В.А., Юдин А.В., РГАТА. Рыбинск, 1997. – Ч1. 79 с.
3. Справочные материалы https://www.mathworks.com, https://matlab.ru
4. Дьяконов В. П. MATLAB 7.*/R2006/R2007: Самоучитель. – М.: ДМК Пресс, 2008. – 768 с.: ил.