В данной курсовой работе для решения создавшейся проблемы были приглашены специалисты высокого уровня, которые отвечали на определенные вопросы.
1. Безусловно, эта проблема очень важна, и ее необходимо решить за короткий период. Но, учитывая экономико-политическую ситуацию страны на данный период, ее решить за короткий срок невозможно. (В политическом плане – война в Чечне, в экономическом – августовские события и огромный внешний долг.)
2. Задача (написать ответ!!!)
3. Однозначно на этот вопрос ответить сложно, потому, как необходимо знать условия функционирования порта. Но я придерживаюсь мнения, что это возможно. Учитывая, что порт морской, то глубины на море будут позволять подходить к причалам порта суда и с такой большой грузоподъемностью (во внимание берется осадка судна при такой загруженности).
4. Я считаю, что имеются.
5. На мой взгляд, нет, потому, что основная проблема заключается не в квалификации кадров организации (хотя проблема квалификации работников фирмы «Олкрет» существует), а в привлечении иностранного капитала. Ведь инвесторы отказались от дальнейшего сотрудничества с фирмой «Олкрет» по причине военных действий в Чечне, а не по поводу не квалифицированности работников.
6. Нет, не сможет. Если бы это было в силах самой фирмы, то в привлечении иностранного капитала не было бы необходимости.
Итак, подходим к непосредственному решению задачи. Для этого прибегаем к использованию методики эвристического прогнозирования.
Составим матрицу, где рассматриваются варианты ответов экспертов (в том числе и собственных).
Вопросы в анкете являются альтернативного характера. Поэтому используем элементы дисперсионного характера.
P = M / N, где М – число единиц (положительные ответы)
N – общее число параметров.
Q = L / N, где L – число нулей (отрицательные ответы)
P + Q = 1 s2 = P . Q
Таблица 1
Варианты ответов экспертов по основным вопросам.
| Вопросы Эксперты | P | Q | s2 | |||||||
| I | 0,67 | 0,33 | 0,22 | |||||||
| II | 0,5 | 0,5 | 0,25 | |||||||
| III | 0,83 | 0,17 | 0,14 | |||||||
| IV | 0,5 | 0,5 | 0,25 | |||||||
| V | 0,5 | 0,5 | 0,25 | |||||||
| VI | 0,33 | 0,67 | 0,22 | |||||||
| VII | 0,67 | 0,33 | 0,22 | |||||||
| VIII | 0,33 | 0,67 | 0,22 |
Проведем классификацию ответов экспертов, используя принципы таксономии. Для этого определяем коэффициент близости между ответами. Воспользуемся формулой Роджерса и Танимото.
S = n(1;1)i,j / n(1)I + n(1)j – n(1;1)i,j, где
n(1;1)i,j – число совпадающих единиц между сравниваемыми рядами.
n(1)I – число всех единиц в i – том сравниваемом году
n(1)j – число единиц в j – том сравниваемом ряду
Все последующие расчеты заносим в Таблицу 2.
Таблица 2
| I | - | 0.75 | 0.50 | 0.17 | 0.75 | 0.50 | 0.60 | 0.50 |
| II | 0.75 | - | 0.33 | 0.20 | 0.50 | 0.25 | 0.75 | 0.67 |
| III | 0.50 | 0.33 | - | 0.60 | 0.60 | 0.17 | 0.50 | 0.17 |
| IV | 0.17 | 0.20 | 0.60 | - | 0.20 | 0.00 | 0.40 | 0.25 |
| V | 0.75 | 0.50 | 0.60 | 0.20 | - | 0.25 | 0.40 | 0.25 |
| VI | 0.50 | 0.25 | 0.17 | 0.00 | 0.25 | - | 0.20 | 0.33 |
| VII | 0.60 | 0.75 | 0.50 | 0.40 | 0.40 | 0.20 | - | 0.50 |
| VIII | 0.50 | 0.67 | 0.17 | 0.25 | 0.25 | 0.33 | 0.50 | - |
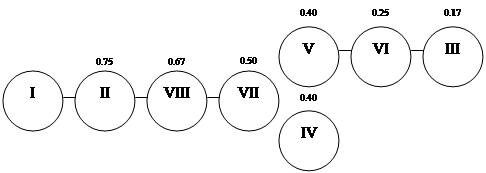
Для обработки этой матрицы существуют разные алгоритмы. Возьмем простейший – метод графов. (Рисунок 1)
 |
|
Итак, мнение экспертов можно представить в следующем виде:
S P
0.75 – I, II 0.40 – V, IV 0.67 – I 0.67 - VII
0.67 – VIII 0.25 – VI 0.50 – II 0.33 - VIII
0.50 – VII 0.17 – III 0.83 – III 0.50 - V
0.50 – IV 0.33 -VI
По этим данным составляем график.
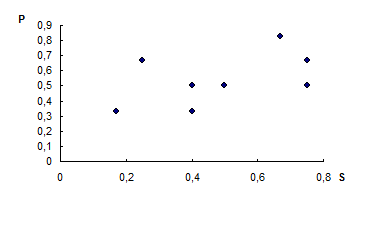
Чтобы определить, насколько существенные различия между мнениями экспертов и сгруппировать их мнение в таксоны составим матрицу коэффициентов Фишера. (Таблица 3)
Коэффициент Фишера определяется через соотношение дисперсий:
F = s2i / s2j
Таблица 3
| I | - | 0.88 | 1.57 | 0.88 | 0.88 | |||
| II | 0.88 | - | 1.78 | 1.14 | 1.14 | 1.14 | ||
| III | 1.57 | 1.78 | - | 0.56 | 0.56 | 0.64 | 0.64 | 0.64 |
| IV | 0.88 | 0.56 | - | 1.14 | 1.14 | 1.14 | ||
| V | 0.88 | 0.56 | - | 1.14 | ||||
| VI | 1.14 | 0.64 | 1.14 | 1.14 | - | |||
| VII | 1.14 | 0.64 | 1.14 | - | ||||
| VIII | 1.14 | 0.64 | 1.14 | - |
Данные этой матрицы сравниваем с критическим значением Fкр = 1,945. Сравнивая коэффициенты Фишера из матрицы с его критическим значением, видим, что эти показатели меньше, следовательно, отличия в мнениях экспертов не существенны и при классификации их можно объединить в один таксон.
Ознакомившись с прогнозной документацией, эксперты предложили свои варианты расчетов, основываясь на благоприятном (Kmin) и неблагоприятном (Kmax) прогнозах. Результаты их прогнозов представлены в таблице 4.
Таблица 4
| Эксперты | Значения характеристик дополнительных капиталовложений (млрд. руб.) | |
| Вариант 1 (Kmin) | Вариант 2 (Kmax) | |
| I | 10.0 | 11.0 |
| II | 9.0 | 12.0 |
| III | 7.0 | 8.0 |
| IV | 8.0 | 12.0 |
| V | 9.5 | 12.0 |
| VI | 8.5 | 11.0 |
| VII | 8.0 | 9.0 |
| VIII |
Проведем анализ полученных данных, определим меры близости мнений экспертов. Результаты расчетов представлены в матрице коэффициентов близости мнений экспертов.
Таблица 5
| I | - | |||||||
| II | - | |||||||
| III | - | |||||||
| IV | - | |||||||
| V | - | |||||||
| VI | - | |||||||
| VII | - | |||||||
| VIII | - |
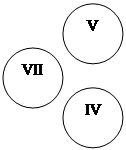
Обработка матрицы производится аналогично обработке матрицы (таблица 2). Получается граф (рисунок 3) с помощью которого строятся таксоны, изображение на графике (рисунок 4).
Таксоны формируются по коэффициентам близости.???????????
 |  |  | |||||||||
 |  |  | |||||||||
Список литературы
1. Виханский О. С., Наумов А. И. Мненджмент: Учебник – 3-е изд. – М: Гардарики, 2002
2.