Модуль 2 Лекция 5
Понятие о теплоёмкости. Теории теплоёмкости газа и конденсированных тел. Методы её оценки на основе экспериментальных данных. Зависимость теплоёмкости от температуры. Зависимость теплового эффекта от температуры и давления. Формула Кирхгофа. Квантовая теория теплоемкости Эйнштейна и Дебая. Понятие о характеристической температуре и методы её оценки на основе экспериментальных данных. Экспериментальные методы исследования теплоёмкости.
Зависимость теплового эффекта реакции от температуры.
Закон Кирхгоффа
В общем случае тепловой эффект химической реакции зависит от температуры и давления, при которых проводится реакция. Влиянием давления на ΔН и ΔU реакции обычно пренебрегают. Влияние температуры на величины тепловых эффектов описывает закон Кирхгоффа:
· Температурный коэффициент теплового эффекта химической реакции равен изменению теплоемкости системы в ходе реакции, т.е. равен разности сумм теплоемкостей продуктов реакции и сумм теплоемкостей исходных веществ..
Продифференцируем ΔН и ΔU по температуре при постоянных давлении и температуре соответственно:
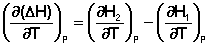 (5.1)
(5.1)
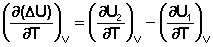 (5.2)
(5.2)
Производные энтальпии и внутренней энергии системы по температуре есть теплоемкости системы в изобарных и изохорных условиях Cp и Cv соответственно:
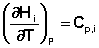 (5.3)
(5.3)
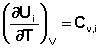 (5.4)
(5.4)
Подставив выражения (5.3, 5.4) в (5.1, 5.2), получаем математическую запись закона Кирхгоффа:
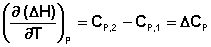 (5.5)
(5.5)
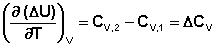 (5.6)
(5.6)
Для химического процесса изменение теплоемкости задается изменением состава системы и рассчитывается следующим образом:
 (5.7)
(5.7)
 (5.8)
(5.8)
Если проинтегрировать выражения (5.5, 5.6) от Т = Т1 до Т = Т2, считая ΔСp (ΔСv) не зависящим от температуры, получим интегральную форму закона Кирхгоффа:
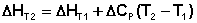 (5.9)
(5.9)
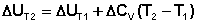 (5.10)
(5.10)
Поскольку обычно известны табличные значения стандартных тепловых эффектов ΔН°298 и ΔU°298, преобразуем выражения (5.9, 5.10):
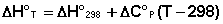 (5.11)
(5.11)
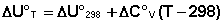 (5.12)
(5.12)
При расчете изменения теплового эффекта реакции в большом интервале температур необходимо учитывать зависимость теплоёмкости от температуры, которая выражается степенным рядом
C°p = a + bT + c׳ T -2 (для неорганических соединений);
C°p = a + bT + cT2 (для органических соединений);
коэффициенты a, b, c приведены в справочниках. Следует отметить, что если ΔCp > 0, то с увеличением температуры растет также и тепловой эффект, а если ΔCp < 0,то с возрастанием температуры тепловой эффект уменьшается.
Теплоемкостью называется количество теплоты, необходимое для повышения температуры вещества на 1 градус. Если теплоемкость относится к 1 г.- удельная (Дж/г К); если к 1 молю вещества – молярная (Дж/моль К), если к 1 г-атому – атомная (Дж/г-атом К). Истинная теплоемкость- количество теплоты (бесконечно малое), которое необходимо для бесконечно малого изменения температуры:
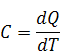 (5.13)
(5.13)
Различают теплоемкость при постоянном давлении Cp (изобарную) и при постоянном объеме Cv (изохорную). Взаимосвязь этих теплоемкостей для идеальных газов определяется соотношением:
Cp = Cv + R, (5.14)
где R – универсальная газовая постоянная, равная 8,314 Дж/моль К.
Из кинетической теории газов вытекает, что внутренняя энергия (U) одноатомного идеального газа равна:
U = 3/2 RT. (5.15)
При повышении температуры одноатомного газа на 1 градус изохорная теплоемкость будет равна:
ΔU = UT+1 – U = 3/2 R (T + 1) – 3/2 RT = 3/2 R, (5.16)
а изобарная теплоемкость
Cp = Cv + R = 3/2 8,314 + 8,314 = 20,789 Дж/моль К. (5.17)
Изобарная и изохорная теплоемкости для твердых и жидких веществ достаточно близки, т.е. с повышением температуры изменение объема последних незначительно.
При расчете теплоемкости следует учитывать, что молекулы одноатомного газа имеют три степени свободы движения атомов в трехмерном пространстве, а двухатомного газа – пять степеней свободы: 3 степени поступательного движения и 2 – вращательного.
Это остается верным для любых линейных многоатомных молекул. Для нелинейных молекул трехатомного газа, а также для молекул более сложного строения, т.е. многоатомных, появляется еще одна степень свободы вращательного движения. Следует отметить, что на каждую степень свободы молекулы при поступательном и вращательном движениях приходится в пересчете на 1 моль газа энергия, равная ½ RT. Отсюда, принимая во внимание известное соотношение (5.15), можем найти теплоемкость при постоянном давлении Cp: для одноатомного газа она равна 5/2R или 20,8 Дж/моль К, а суммы поступательного и вращательного вкладов двухатомных и многоатомных линейных молекул в пересчете на моль идеального газа соответственно равны:
Cp = Cv + R = 5/2R + R = 29,1 Дж/моль К. (5.18)
Cp = Cv + R = 3R + R = 33,26 Дж/моль К. (5.19)
Однако, экспериментальные значения теплоемкости двухатомных и многоатомных газов отличаются от расчетных значений (5.18) и (5.19), т.к. имеют еще дополнительную колебательную составляющую; полное значение изобарной теплоемкости идеальных газов указанного типа выражается соотношением:
Cp = Cv пост. + Cv вращ. + Cv колеб. + R. (5.20)
Природа колебательного вклада в теплоемкость в отличие от поступательного и вращательного значительно сложнее. (см. стр. 18 Пашинкин)
Правило Дюлонга-Пти Согласно этомк правилу атомная теплоемкость простых веществ в твердом состоянии (произведение атомной массы на его удельную теплоемкость) приблизительно одинакова для большинства элементов при комнатной температуре и равна (25,9 – 26,8) Дж/моль К. Однако, правило Дюлонга-Пти строго выполняется для каждого простого вещества лишь при температуре Дебая. Cp ≈ Cv ≈ 26,3 Дж/моль К.
Правило Неймана и Коппа По этому правилу мольная теплоемкость соединений в твердом состоянии приблизительно равна сумме атомных теплоемкостей элементов, входящих в состав данного соединения, если последние не слишком отличаются по своей химической природе.
Интерполяционные уравнения, описывающие температурную зависимость теплоемкости
Экспериментальные значения теплоемкостей индивидуальных веществ при температурах выше 200 К удобно выражать следующими эмпирическими формулами:
Ср = a + bT (5.21)
Ср = a + bT + cT2 (5.22)
Ср = a + bT + cT -2 (5.23)
Коэффициенты, входящие в указанные уравнения, различны по значениям. При T = О коэффициент "а" не имеет смысла теплоемкости, а является лишь экстраполяционной постоянной. Уравнение (5.23) лучше передает зависимость Ср от Т при высоких температурах в связи с тем, что вклад третьего члена в общую сумму уменьшается. При этом зависимость Ср от Т становится почти линейной, а при сравнительно низких температурах (сТ-2) возрастает, и данная зависимость становится криволинейной, что согласуется с опытными данными. Поэтому небольшая экстраполяция в области высоких и низких температур не связана с большой погрешностью. А небольшая экстраполяция в случае уравнения (5.22) может привести к значительным отклонениям, так как при высоких температурах вклад члена сТ2 в общую теплоемкость большая, что приводит к преувеличенным результатам, или (если С < О) кпоявлению максимума, не имеющего физического смысла. Тем не менее в справочниках часто встречаются оба эти уравнения.
Для небольшого интервала температур, а также для описания зависимости теплоемкости между температурами полиморфных превращений можно пользоваться уравнением (5.21). Этому уравнению отвечает температурная зависимость теплоемкости твердых веществ при температурах, превышающих температуру Дебая ΘД.