3.1. ИСПЫТАНИЕ НА КРУЧЕНИЕ СТАЛЬНОГО И ЧУГУННОГО ОБРАЗЦОВ
Цель работы: изучить процесс разрушения стали и чугуна при кручении и определить их механические характеристики.
О борудование и инструменты: испытательная машина КМ-50; образец стали и чугуна - 2 шт; штангенциркуль.
Теоретические предпосылки. Кручение осуществляется двумя равными и противоположно направленными крутящими моментами, которые прикладываются к концам образца в плоскостях, нормальных к его продольной оси.
Максимальные касательные напряжения при кручении действуют в плоскостях, перпендикулярных к оси образца, нормальные - под углом 45º. К ней. После разрушения от среза стали и отрыва чугуна получаются характерные формы излома (рис.3.1), по которым можно однозначно определить характер разрушения. Это объясняется тем, что чугун слабо сопротивляется растяжению, и разрушение материала происходит по винтовой поверхности, наклоненной под углом 45о к образующей (рис. 3.1, б). Разрушение стали при кручении происходит от среза по поперечному сечению (рис.3.1, а).
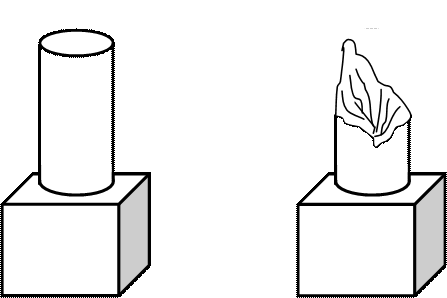
а) б)
Рис 3.1
В области упругой деформации касательные напряжения для цилиндрического образца определяют по формуле:
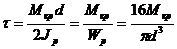 .
.
Формула дает хорошие результаты по упругой деформации и не пригодна при пластическом течении материала. Предел прочности после больших пластических деформаций определяется по формуле, учитывающей поправку на пластическую деформацию: 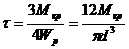 .
.
Деформация при кручении определяется углом закручивания, который в пределах упругих деформаций связан с нагрузкой, т.е. с крутящим моментом, линейной зависимостью 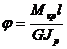 ,
,
где Мкр - крутящий момент; l - длина вала; G - модуль упругости материала при сдвиге (модуль упругости второго рода); JP - полярный момент инерции площади поперечного сечения вала, d - диаметр вала,
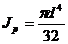 .
.
Указанная пропорциональность между нагрузкой и деформацией наблюдается в начальной стадии кручения образца, затем, так же как при растяжении или сжатии, пропорциональность нарушается и наступает быстрое увеличение утла закручивания при незначительном увеличении крутящего момента.
На рис. 3.2.а показана диаграмма кручения для малоуглеродистой стали, а на рис. 3.2.б - диаграмма для чугунного образца приблизительно тех же размеров (чугун не подчиняется закону пропорциональности).
Модуль G связан с модулем упругости первого рода Е следующим соотношением G = E/2(1+μ), где μ - коэффициент Пуассона.

а) б)
Рис.3.2
Порядок прове д ения работы.
1. Сделать эскиз образца с указанием размеров его рабочей части.
2. Вычислить полярный момент сопротивления поперечного сечения образца:

3. Произвести наблюдения за процессом испытания стального и чугунного образцов, записать крутящие моменты и утлы закручивания, соответствующие моменту разрушения образцов.
4. Вычислить пределы прочности при кручении:
для стали  ,
,
для чугуна 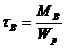 .
.
5. Сделать зарисовку частей испытанных образцов с указанием характерных особенностей разрушения.
Содержание отчета.
1. Название и цель работы.
2. Теоретические предпосылки (по желанию).
3. Эскиз образца до испытания и зарисовки частей испытанных образцов.
4. Таблицу опытных данных, расчеты момента сопротивления и пределов прочности.
5. Пояснение характера разрушения стали и чугуна.
6. Выводы по работе.
| Материал образца | d, мм | Wp3, м3 | МB, Кг·м | φB, град | τв , МПа | Характер разрушения |
| Сталь | ||||||
| Чугун |
Контрольные вопросы:
1. Какие напряжения возникают в сечениях, расположенных перпендикулярно к оси образца и наклонных под углом 45º?
2. Как по характеру разрушения образца определить, какой вид напряжений наиболее опасен для данного материала?
3. Как определяется и от чего зависит деформация при кручении?
4. Что характеризует произведение GJP?
ЖЕСТКОСТЬ ПРУЖИНЫ
Цель работы: Экспериментально определить жесткость пружины; сравнить результаты расчета пружины на прочность по точным и приближенным формулам.
Оборудование и инструменты: Испытательная машина МИП-100-2; цилиндрическая винтовая пружина; штангенциркуль; индикатор часового типа 0-10 мм.
Теоретические предпосылки:
Расчет цилиндрических пружин (рис.7.1), сжатых или растянутых силой Р, проводится по формулам
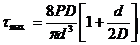 ,
,
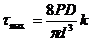 , где
, где 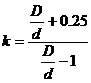 ,
,
где τmax - касательное напряжения, D - диаметр пружины, d - диаметр прутка (см. рис. 3.3)
Осадка пружины (λ) под действием силы Р определяется по формуле
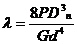 .
.
Иначе λ = P/C, где 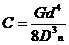 ,
,
где G – модуль сдвига материала пружины, [МПа], n – число витков пружины.
Величина С, равная нагрузке, вызывающей осадку λ = 1см. называется жесткостью пружины. Приведенные формулы справедливы для цилиндрических пружин с малым шагом витков, - если угол навивки α =10о - 15º. (рис.7.1) Очевидно
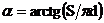 ,
,
где S - шаг пружины (расстояние между центрами соседних витков пружины).

Рис. 3.3
Порядок проведения работы.
1. С помощью штангенциркуля найти размеры пружины D, d, L и S (рис.3.3). Определить число витков как n=L/S, найти угол α.
2. Установить пружину между тарелками машины МИП-100-2, нагрузить вручную усилием Р=5 кг. Установить индикатор, проследив, чтобы показание стрелки находилось в пределах 0.5- 1.2 мм, снять «нулевой» отсчет.
3. Увеличивая нагрузку равными ступенями Р=5 кг. До 5×6=30кг, измерять осадку λ=A1 – A0. Данные измерений заносить в таблицу.
| i | Pi | A1 | λ=A1 – A0 | Δλ1 |
| λ1 = λ0 | ||||
| λ2 = λ1 | ||||
| λ3 = λ2 | ||||
| Σ Δλi | Δλy=1/3 ΣΔλy |
4. Построить график зависимости λ= λ(Р)(так называемую характеристику пружины), выбрав масштаб таким образом, чтобы угол наклона прямой к оси абсцисс был близок к 45º.
5. По данным опыта найти жесткость пружины С как C оп =ΔP/Δ λср, [Н/м].
6. Определить модуль упругости материала G, [МПа]: 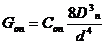 , cравнить полученное значение G с табличным.
, cравнить полученное значение G с табличным.
7. Определить погрешность, %.
8. Определить максимальные касательные напряжения в сечениях пружины, приняв Р= 500 Н.
Содержание отчета.
1. Название и цель работы.
2. Перечень приборов к инструментов.
3. Эскиз пружины с размерами α, n.
4. Таблица.
5. График λ= λ(Р).
6. Вычисление Con.
7. Вычисление Gon и сравнение с G табличным.
8 Подсчет τ max.
Контрольные вопросы.
1 Что называют шагом пружины?
2. Как измерить шаг пружины?
3. Как измерить диаметр пружины?
4. Что называется жесткостью пружины?
5. Как производится расчет пружины на прочность''
6. Как измеряется осадка пружины?
7. Что называется характеристикой пружины?
3.3. КОСОЙ ИЗГИБ
Цель работы - определить величину и направление прогиба свободного конца консоли при косом изгибе; сравнить опытное значение прогиба с теоретическим.
Инструменты и приспособления: Стальная консоль прямоугольного сечения, штангенциркуль, металлическая линейка длиной 1000 мм. (500 мм), два индикатора часового типа 0-10 мм, набор гирь 0.5 кг и 1 кг.
Теоретические предпосылки. Если плоскость действия внешних сил (υOz) при изгибе призматической балки (рис. 3.4) не лежит не в одной из ее главных плоскостей инерции (уOz, хOz), то направление прогибов, вообще говоря, не совпадает с плоскостью действия сил (υOz). Поэтому этот вид деформации называется косым изгибом. Для определения прогибов балки и напряжений в ее поперечных сечениях в этом случае пользуются принципом независимости действия сил.
Очевидно, что в случае изгиба консольной балки прямоугольного поперечного сечения силой, приложенной к свободному концу (рис. 3.4) наибольшее нормальное напряжение в сечении Z = 0, прогибы fx и fy полный прогиб f и его направление могут быть определены по формулам:
max σ = 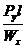 +
+  =
=  +
+ 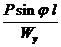
fy = 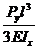 =
= 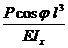 ; fx =
; fx =  =
= 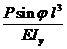 ; f =
; f = 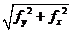
tg α= 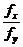 =
= 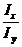 · tg φ=
· tg φ= 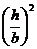 · tg φ
· tg φ
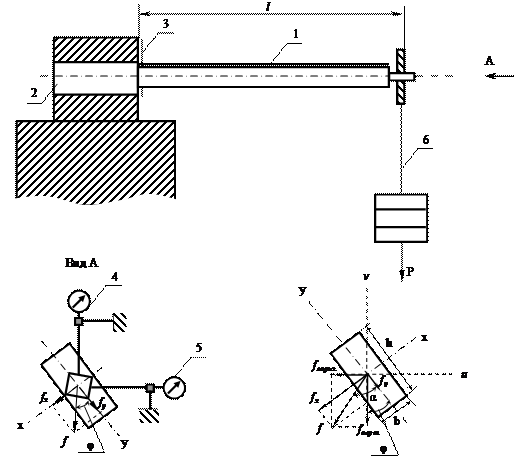
Рис. 3.4.
Установка для проведения опыта представляет собой закрепленную на массивной тумбе стальную консольную балку 1 прямоугольного поперечного сечения, снабженную цилиндрическим утолщением 2 в месте заделки (рис. 3.4.). Это позволяет поворачивать плоскость симметрии балки yOz на любой угол φ по отношению к вертикали (к линии действия силы Р). Отсчет угла φ производится по шкале 3. Индикаторы 4, 5 закрепленные на штативах, служат для измерения вертикальной fυ и горизонтальной fw составляющих перемещения f свободного конца балки. Нагружение балки производят при помощи подвески 6 и набора гирь 7.
Порядок проведения работы.
1. Измерить и записать необходимые размеры l, b, h, φ.
2. Вычислить геометрические характеристики сечения балки: Iy, Iх, Wy, Wx.
3. Загрузить подвеску начальным грузом, равным 1 кг. (Предварительная загрузка устраняет зазоры в креплениях и обеспечивает более стабильную работу измерительных приборов).
4. Выставить показания индикаторов на нули.
5. Постепенно добавляя гири, ступенчато увеличивать нагрузку с шагом ∆Р=1кг(10Н).
6. После каждого увеличения нагрузки снимать показания индикаторов и результаты заносить в таблицу.
7. Определить величины вертикальных fверт. и горизонтальных fгориз. прогибов:
fiверт.=Ui1 – Ui-11; fiгориз.=Ui2 – Ui-12
где Ui1,(Ui2) - показания индикатора 1 (2) после і-го опыта.
8. Определить cредние величины прогибов fверт и fгориз..
9. Найти полный прогиб:
опытную величину fоп= 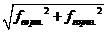
теоретическую величину fт= 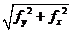
9. Определить погрешность: ∆= 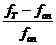 ·100%
·100%
Содержание отчета.
1. Название и цель работы.
2. Теоретические предпосылки (по желанию).
3. Эскиз установки с необходимыми размерами.
4. Вычисление геометрических характеристик сечения балки: Jx, Jy, Wx, Wy.
5. Вычисление fy, fx
6. Таблица измерений.
7. Сравнение fоп. и fт (∆%).
Контрольные вопросы.
1. Какой вид деформации называется косым изгибом?
2. При каких условиях применим принцип независимости действия сил?
3. Во сколько раз перемещение fх. больше fу, если
а) отношение размеров сечения h/b = 3, а угол φ = 45о(рис.3.4)?
б) отношение h/b = 10, угол φ = 6о.
4. При каких условиях направление прогиба балки f всегда лежит в плоскости действия силы Р?
5. Почему рекомендуется первый отсчет по индикаторам производить при небольшой нагрузке, а не при нагруженной балке?
6. В каких пределах изменяется полный прогиб f при изменении угла φ от 0 до 90 гр?
7. Укажите положение нейтральной линии на чертеже.
8. Уравнение нейтральной линии.
9. Условие прочности при косом изгибе.
Лабораторная работа № 4
4.1. ОПРЕДЕЛЕНИЕ ПРОГИБОВ И УГЛОВ ПОВОРОТА СЕЧЕНИЙ БАЛКИ НА ШАРНИРНЫХ ОПОРАХ
Цель работы: Проверить формулы для определения прогибов и углов поворота сечений балки по методу Верещагина.
Оборудование и инструменты: Установка СМ-5, штатив, индикатор часового типа 0-10 мм, набор гирь 0.5-1 кг, штангенциркуль, измерительная линейка.
Теоретические предпосылки. Определение перемещений в системах, состоящих из прямолинейных элементов постоянной жесткости, можно значительно упростить путем применения приема вычисления интеграла Мора, называемого способом перемножения эпюр или методом Верещагина. Данный метод заключается в следующем.
Строится грузовая эпюра изгибающих моментов от всех внешних нагрузок, действующих на балку. В точке, прогиб которой определяется, прикладывается единичная сила Р=1 и строится единичная эпюра изгибающих моментов, возникающих в результате ее действия. Для определения прогиба сечения балки применяется формула Верещагина:
∆= 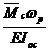 ,
,
где ωр- площадь грузовой эпюры изгибающих моментов;
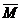 с - ордината единичной эпюры, соответствующая центру тяжести грузовой эпюры;
с - ордината единичной эпюры, соответствующая центру тяжести грузовой эпюры;
Е - модуль Юнга материала балки (модуль упругости І рода);
І ос- осевой момент инерции поперечного сечения балки.
Методика определения угла поворота сечения балки аналогичная описанной, за исключением того, что в сечении угол поворота которого определяется, прикладывается единичный момент 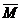 = 1.
= 1.
Применим метод Верещагина для определения прогиба и угла поворота сечения балки, рассматриваемой в данной работе. А именно, определим прогиб точки С и угол поворота D (см. рис. 4.1).
После построения грузовой М и единичных 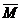 i эпюр (от действия соответственно единичной силы
i эпюр (от действия соответственно единичной силы 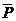 = 1, приложенной в точке С, и единичного момента
= 1, приложенной в точке С, и единичного момента 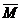 = 1, приложенного в точке D), используем формулу (4.1.).
= 1, приложенного в точке D), используем формулу (4.1.).
Для определения прогиба точки С она примет вид:
Δс= 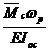 =
= 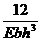 (
(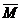 с1·ωр1+
с1·ωр1+ 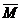 с2 ωр2) =
с2 ωр2) = 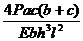 (а 2+
(а 2+  ). (4.1)
). (4.1)
Для определения угла поворота сечения D формула выразится:
ΘD = 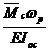 =
= 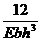 (
(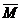 c1·ωр1+
c1·ωр1+ 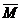 с2 ωр2)=
с2 ωр2)= 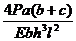 (а 2+
(а 2+  ). (4.2)
). (4.2)
Таким образом после подстановки в формуле (4.1) и (4.2) значений Е, Р и размеров балки, мы получим величины прогиба Δс и угла поворота ΘD.
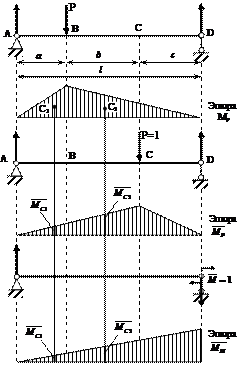
Рис. 4.1
Установка для проведения опыта (рис. 4.2) представляет собой стальную балку 1 прямоугольного поперечного сечения, расположенную на двух опорах. Для нагружения балки в любой точке служит передвижная подвеска 2, на которую кладутся гири. При этом замеры прогибов балки в нужной точке производится индикатором 3, закрепленном на передвижном штативе 4. Для определения углов поворота крайних сечений балки в этих точках предусмотрена возможность измерения поворота сечения с помощью индикатора 5 по схеме, изображенной на рис. 4.3. В результате угол поворота сечения определится из выражения:
tgΘ » Θ = ΔDгор / hD (4.3)
где ΔDгор.- показания индикатора 5, мм; hD= 150 мм.
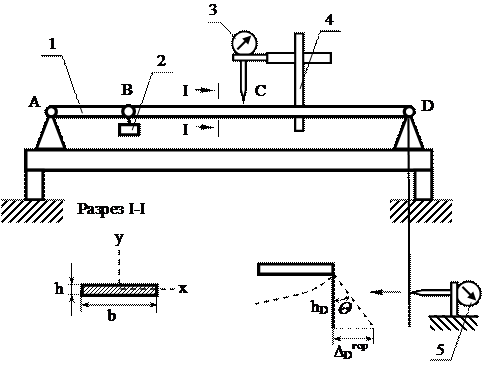
Рис. 4.3
Порядок проведения работы.
1. Измерить необходимые размеры балки: b, h, l, а, b, с.
2. Установить в точке В подвеску с начальным грузом Ро = 0,5 кг. Показания индикаторов, при этом, выставить на нули.
3. Постепенно добавляя гири, ступенчато увеличивать нагрузку с шагом ΔР=1кг(=10Н).
4. После каждого увеличения нагрузки снимать показания индикаторов и результаты заносить в таблицу.
5. Определить величины прогибов ∆сі и ∆Di:
Δci=ui(3) – ui-1(3), ΔDiгор = ui(5) – ui-1(5),
где ui(3) , ui(5)- показания индикаторов 3 и 5 после і - того опыта.
6. Определить средние величины ∆с и 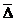 D гор .:
D гор .:
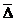 с =
с = 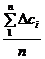 ,
, 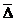 D гор =
D гор = 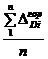 ,
,
где n - число опытов.
7. Записать опытные величины прогиба сечения и угла поворота сечения D:
Δсоп = 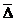 с, ΘDon=
с, ΘDon= 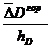
8. Используя формулы (4.1) и (4.2) определить теоретические значения Δст и ΘD т при Р = 10Н и сравнить их с опытными.
Содержание отчета.
1. Название и цель работы.
2. Теоретические предпосылки (по желанию).
3. Результаты измерений и вычислений, выполненных согласно раздела 5.
4. Итоговая таблица.
5. Выводы по работе.
Контрольные вопросы.
1. Какие способы определения прогибов при изгибе балки Вы знаете?
2. Каковы пределы применимости формул для определения прогибов и углов поворота сечений при изгибе?
3. Запишите формулу Верещагина.
4 Объясните отличие применения метода Верещагина при определении прогиба, с одной стороны, и угла поворота сечения балки, с другой.
| № опыта | Рi, кг | ΔРi, кг | ui(3), мм | Δсi, мм | ui(5), мм | ΔDiгор, мм |
| 0,5 | ||||||
| 1,5 | ||||||
| 2,5 | ||||||
| 3,5 | ||||||
4.2. ОПРЕДЕЛЕНИЕ МОМЕНТА ЗАЩЕМЛЕНИЯ В СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ БАЛКЕ.
Цель работы: Определение реактивного момента, возникающего в заделке в статически неопределимой балке и сравнение опытных данных с теоретическими.
Приборы и инструменты: Установка СМ-5, индикатор часового типа, гири 1 кг, штангенциркуль.
Краткие теоретические предпосылки.
Балки, внутренние усилия в которых не могут быть найдены из одних только уравнений равновесия статики, называются статически неопределимыми. Наиболее общим методом раскрытия статической неопределимости стержневых систем является метод сил, который заключается в том, что заданная статически неопределимая система мысленно освобождается от дополнительных связей, а их действие заменяется силами и моментами. Система, освобожденная от дополнительных связей, становится статически определимой и носит название основной системы. Для каждой статически неопределимой системы можно выбрать несколько основных систем.
Рассмотрим однопролетную балку, защемленную одним концом (рис.4.4 а). Эта балка один раз статически неопределима, поскольку неизвестных четыре (VА, Vb, НА, MА), а независимых уравнений статики можно составить три (ΣХі=0, ΣYi=0, ΣМА=0).
На рис. 4.4б и 4.4в представлены две основных системы. Для решения задачи необходимо составить уравнение совместности деформации, выражающие ту мысль, для обеспечения эквивалентности заданной и основной системы перемещения точки В или А под действием заданной нагрузки Р и силы Х должно быт равны нулю:
Хіdіх + Δір=0.

Рис.4.4
Определение перемещения σіх и Δір можно выполнить одним известным способом (универсальное уравнение, интеграл Мора, способ Верещагина)
Решение основной системы, представленной на рис. 4в, дает следующее значение момента защемления:
МА = Хі = 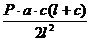 .
.
После нахождения неизвестной реакции Хі система становится статически определимой и построение эпюр изгибающих моментов и поперечных сил может быть произведено обычным способом.
Опытная установка СМ-5, на которой выполняется работа (рис. 5) представляет собой стальную балку прямоугольного сечения 1, шарнирно опертую на двух опорах (рис. 4.5). Нагружение балки может быть произведено в любой точке сосредоточенными силами (грузами) посредством подвижного подвеса 2. На левой опоре балки шарнирно закреплены рычажок 3 и грузовой рычаг 4 с подвижными грузами 5, которые поворачиваются при повороте сечения балки на опоре. Рычажок 3 служит для измерения угла поворота сечения балки с помощью индикатора 6. Поворот сечения балки вызывается сосредоточенной нагрузкой-грузами, укладываемыми на подвес 2.
После нагружения балки и взятия отсчета по индикатору, необходимо создать реактивный момент, имитирующий защемление балки на левой опоре, что достигается путем перемещения подвижного груза 5 по рычагу 4 на некоторое расстояние (плечо) - l r. Величина плеча определяется условием возврата стрелки индикатора в начальное положение.
Порядок проведения работы:
1. Измерить длину и поперечное сечение балки.
2. Установить подвес 2 в заданной точке с координатой х = а.
3. Взять начальный отсчет по индикатору 6.
4. Нагрузить балку - положить на подвес груз в 1 кг.
5. Плавно переместить груз 5 влево (и тем самым создать защемление на левой опоре) на некоторую величину l r, соответствующую моменту возврата стрелки индикатора в начальное 6 положение;
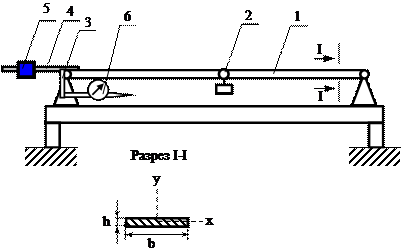
Рис 4.5.
6. Пользуясь делениями на рычаге 4, определить величину l r, зафиксировать вес груза R.
7. Разгрузить балку.
8. Данные опыта записать в таблицу и произвести их обработку.
9. Вычислить величину реактивного момента МА = R l p (H·м).
10. Опыт повторить не менее 3-х раз и вычислить среднее значение МАср;
11. Выбрать основную систему статически неопределимой балки, соответствующую опытной установке и вычислить величину момента защемления МАт;
12. Произвести сравнение опытной и расчетной величин момента защемления балки
δ= 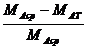 ·100%
·100%
Содержание отчета.
1. Название и цель работы.
2. Теоретические предпосылки (по желанию).
3.Результаты измерений и вычислений.
4. Итоговая таблица.
5. Выводы по работе.
Контрольные вопргосы.
1. Что такое статически неопределимая система?
2. Чему равна степень статической неопределимости?
3. В чем заключается метод сил?
4. В чем отличие заданной и основной систем?
5. Запишите канонические уравнения для n статически неопределимой системы.
4.3. ПОТЕРЯ УСТОЙЧИВОСТИ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ С ОБРАЗОВАНИЕМ КОЛЬЦЕВОЙ СКЛАДКИ ПРИ ОСЕВОМ СЖАТИИ.
Цель работы: Ознакомиться с задачей об устойчивости цилиндрической оболочки, сжатой в осевом направлении; видами потери устойчивости сжатых оболочек; определить критическое значение сжимающего напряжения.
Инструменты и приспособления: Гидравлический пресс РИИТ-30, образец (цилиндрическая тонкостенная груба), штангенцирпкуль.
Теоретические предпосылки. Пример потери устойчивости прямолинейной формы равновесия центрально-сжатого стержня, не является единственным. Большой практический интерес представляют такие виды потери устойчивости, при которых изменяется не только форма сжатого тела, но и формы и размеры его поперечного сечения. Примером этого может служить потеря устойчивости центрально-сжатой цилиндрической тонкостенной оболочки с образованием кольцевой складки.
Тонкостенной цилиндрической (осиметричной) называется оболочка, имеющая форму тела вращения, толщина которой весьма мала по сравнению с радиусом кривизны ее поверхности.
Проанализируем условие образования кольцевой складки при потере устойчивости сжатой цилиндрической заготовки
Момент начала образования кольцевой складки соответствует моменту возникновения пластического изгиба в продольном сечении оболочки (рис.6). Таким образом, задача сводится к определению величины максимальных сжимающих напряжений, под действием которых возникает изгиб.
Согласно условия упругости равновесия очевидно, что моменты, действующие по принципам участка изгиба от сил, образованными напряжениями, уравновешиваются моментом М, величину которого можно определить по формуле, полученного в теории напряженного состояния:
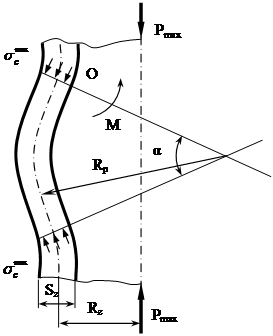
Рис. 4.6
М=  ·Rz, (1)
·Rz, (1)
где: Sz, Rz - толщина и срединный радиус оболочки, σт – напряжение текучести материала оболочки, σсmax – максимальное сжимающее напряжение,
Уравнение равновесия моментов относительно точки О (рис. 4.6) запишется в виде:
σсmaxSzRzRr - σсmaxSzRz Rr cosα =  ·Rz,
·Rz,
(σсmax)2Sz + σсmax4σт(1 – cosα) Rr – σт2Sz = 0,
σсmax =  . (2)
. (2)
При этом мы привели его к квадратному виду и решили.
Перепишем равенство (2), сделав замену Rr = lu /α,
σсmax = 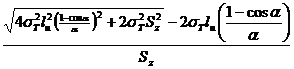 . (3)
. (3)
Так как нам необходимо найти величину напряжения σсmaxв начальный момент пластического изгиба (начало образования кольцевой складки), то принимаем угол поворота сечения участка свободного ига иба α - 0.
С учетом этого, используя правило Лопиталя, получим:
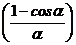 =0 =0
| |
| lim | |
 α→0 α→0
| |
σсmax = σт (4)
Таким образом, получим, что величина сжимающею напряжения, вызывающего потерю устойчивости с образованием кольцевой складки, по абсолютному значению может быть принята равной напряжению текучести материала оболочки.
Порядок проведения работы.
1. Измерить толщину стенки и средний радиус образца: Sz, Rz.
2. Поместить образец между опорными плитами гидропресса и подвергнуть сжатию, зафиксировав значение критической силы Рmax, вызывающей потерю устойчивости.
3. Расчитать опытное значение максимального (критического) сжимающего напряжения: σсmax= Рmax/А, где А =2pRzdz — площадь поперечного сечения образца.
4. Сравнить подученное значение сжимающего напряжения с напряжением текучести материала оболочки:
d=  ·100%
·100%
Содержание отчета.
1. Название и цель работы.
2. Теоретические предпосылки (по желанию).
3. Результаты измерений и вычислений, выполненных согласно раздела 4.
4. Выводы по работе.
Контрольные вопросы.
1. Какова цель работы?
2. Что называется устойчивостью?
3. Что называется тонкостенной осиметричной оболочкой?
4. Чему равно критическое сжимающее напряжение?
4.4. ОПЫТНОЕ ИЗУЧЕНИЕ РЕЗОНАНСА ВАЛА
Цель работы: Опытное изучение резонанса вала и определение его критической частоты вращения (nкр).
Оборудование и инструменты: Установка ДМ-36, штангенциркуль 0-250 мм, масштабная линейка 0-500мм.
Теоретические предпосылки. Как известно критической называется частота вращения вала, равная частоте собственных поперечных его колебаний nкр. В этом случае величина прогиба вала растет неограниченно, т.е. имеет место явление резонанса или потери динамической устойчивости вала. Такие частоты вращения вала, при отсутствии или малых силах сопротивления, например, когда система работает в воздушной среде, приводит к резко ненормальной работе системы и их следует избегать на практике. Необходимо, как говорят, «отстроиться от резонанса» вала. Пусть О - центр тяжести диска, посаженного на вал длиной l (рис. 4.7) ОО1= е - небольшой эксцентриситет, всегда имеющий место, даже при самой точной сборке и балансировке вала. Тогда при вращении вала с их частотой w он будет подвергаться изгибу центробежной силы Р равной:
РU = 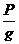 ·w2(l + y), (1)
·w2(l + y), (1)
где: Р - вес диска, у — прогиб вала в сечении, где насажен диск, g — ускорение силы тяжести, w- частота вращения вала или круговая частота вынужденных колебаний вала (рад/с).
Известно, что w= pn/30, (2)
где n— частота вращения вала (об/мин).
Для прогиба у в месте приложения силы РU можно записать
у =dn РU= dn 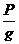 (l + y) w2, (3)
(l + y) w2, (3)
где: dn - прогиб в точке приложения силы РU по направлению этой силы, вызванной статическим приложением единичной силы РU=1.
Решая полученное уравнение (3) относительно прогиба у получаем:
у = 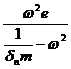 =
= 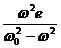 . (4)
. (4)
Здесь w0 – собственная круговая частота поперечных колебаний вала (рад/с), m= РU /у – масса диска.
w0 = 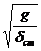 , (5)
, (5)
где: dст - статический прогиб вала под силой Р.
Из уравнения (4) видно, что при w=w0 у →¥, т.е. в этом случае динамическая устойчивость вала нарушается. w=w0 через n кр и имея в виду равенства (2) и (5) получаем
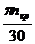 =
= 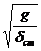 . (6)
. (6)
Откуда
n кр= 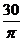
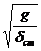 »
»  (7)
(7)
Равенство (7) справедливо, если пренебречь массой вала по сравнению с массой диска, и если отсутствуют силы сопротивления вращению диска или ими можно пренебречъ.
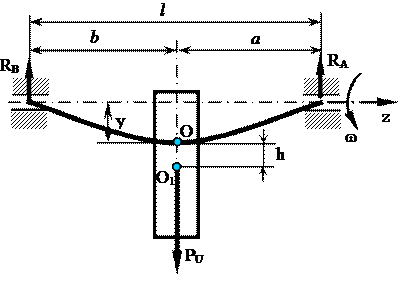
Рис. 4.7

Рис. 4.8
Схема установки (рис. 4.8)
На вал 1 постоянного круглого сечения диаметром d и длиной l посажен диск 2. Вал установлен в подшипниках 4 и 5 и соединен с валом мотора 2 при помощи гибкой муфты 6. Частота вращения вала мотора, а следовательно и вала 1, может меняться при помощи реостата 7. Для предотвращения резкого «биения» вала при роторе на динамической устойчивости установлены ограничители 8и 9. Частота вращения вала фиксируется тахометром 10. С точки зрения расчета, вал представляет собой балку на двух шарнирных опорах нагруженную силой Р, поэтому статический прогиб вала под силой Р будет
dст=  (8)
(8)
Jx – осевой момент инерции сечения вала,
Е – модуль нормальной упругости материала вала (Е = 2·105 Мпа)
Jx= 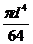 . (9)
. (9)
Если диск расположен по середине пролета вала, то а = b = 0,5 и учитывается собственный вес вала Q, то
dст= 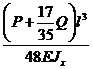 (10)
(10)
Порядок проведении работы.
1. Записываются данные для опыта и расчета: материал вала, модуль нормальной упругости: Е, [МПа], диаметр вала: d, [м], осевой момент инерции сечения вала: Jx= 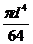 , вес диска Р, [Н]:
, вес диска Р, [Н]:
Р+0,3=
Р+0,6=
По формулам (8) и (10) или по (8) с учетом собственного веса вала, вычисляют прогиб dст вала под диском, dст [м], от грузов Р, Р+0,3 и Р+0,6.
По формуле (7) подсчитываются расчетные значения критической частоты вращения вала nкр, n1кр, n2кр.
2. Выключается мотор и при помощи рукоятки реостата, на панели приборов медленно увеличивают число оборотов мотора, фиксируемое тахометром. Вал, сначала работающий спокойно, по мере приближения к резонансной частоте вращения начинает вибрировать. Когда n→nкр амплитуда колебаний вала достигает максимума и на панели приборов зажигается зеленая лампочка «Резонанс». По тахометру необходимо заметить число оборотов nн при этом. Когда это произошло, следует быстро, небольшим рывком, увеличить число оборотов мотора одновременно нажимая на кнопку гашения лампочки «Резонанс». Если она погасла, это свидетельствует о прохождении «Резонанса». Вал начинает вращаться спокойно, «Резонанс» пройден, амплитуда его колебаний уменьшается.
3. Обратным медленным вращением рукоятки реостата следует постепенно уменьшать частоту вращения вала, вал вновь войдет в «Резонанс», но уже при уменьшении закритической частоты вращения. Следует заметить это число оборотов nв, когда загорится лампочка «Резонанс», кнопка управления которой также все время нажата рукой. И вновь рывком следует уменьшить число оборотов вала при прохождении «Резонанса».
4. Записать среднее число оборотов вала
nкр=nн + nв/2
при данной величине груза Рн его положении на валу.
5. Повторить действие согласно пп. 2-4 для грузов P + 8H и P + 6H
6. Сравнить опытные числа критических частот вращения вала с расчетными для заданной величины веса диска и его положения на валу, установив относительную погрешность в %
(nкр. теор. - nкр. опыт./ nкр. теор.)×100%
7. Сделать выводы.
Содержание отчета
1. Наименование работы.
2. Цель работы.
3. Оборудование и инструменты.
4. Краткие теоретические сведения (по