ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ДИФФУЗИИ ПАРОВ ВОДЫИ СПИРТА В ВОЗДУХЕ
Цель работы: экспериментальное определение коэффициента диффузии паров воды и спирта в воздухе.
Литература: [4] гл. 5 §§ 5.1-5.3; [7] гл. 7 §§ 7.1-7.3; [19] гл. 6 §§ 6.2-6.3.
Приборы и принадлежности: электронные аналитические весы, фторопластовая подложка, шприцы с водой и со спиртом, секундомер.
ВВЕДЕНИЕ
Диффузией называется явление проникновения двух соприкасающихся веществ друг в друга. В данной работе определяют коэффициент диффузии водяных паров и спирта в воздухе при испарении капли воды и спирта, считая диффузию стационарной.
Масса пара 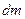 , диффундировавшего через площадку dS за время dt, определяется уравнением Фика:
, диффундировавшего через площадку dS за время dt, определяется уравнением Фика:
 , (1)
, (1)
где  – градиент плотности водяного пара, D – коэффициент диффузии.
– градиент плотности водяного пара, D – коэффициент диффузии.
Капля на несмачивающей подложке принимает в поле тяжести сплюснутую форму, которую для простоты будем считать полусферической. В стационарных условиях поток массы через полусферу произвольного радиуса r постоянен и равен
 . (2)
. (2)
Отсюда следует, что
 . (3)
. (3)
Из (3) можно найти градиент плотности пара:
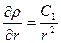 . (4)
. (4)
Подставив (4) в уравнение диффузии (1), получим:
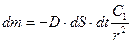 . (5)
. (5)
Для определения постоянной С 1 запишем закон изменения плотности 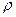 паров от расстояния r. Интегрируя (4), получаем:
паров от расстояния r. Интегрируя (4), получаем:
 . (6)
. (6)
Постоянную С 2 найдем из краевых условий задачи. Внутри капли плотность воды не изменяется с изменением  . На расстояниях
. На расстояниях  >>
>>  , где
, где  – радиус капли, плотность паров убывает согласно уравнению (6) (график
– радиус капли, плотность паров убывает согласно уравнению (6) (график 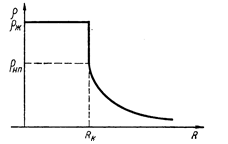 изменения плотности изображен на рисунке), причем при
изменения плотности изображен на рисунке), причем при  ®Ґ
®Ґ 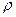 ®
®  , где
, где  - относительная влажность воздуха, rн.п. – плотность насыщенных паров. Отсюда
- относительная влажность воздуха, rн.п. – плотность насыщенных паров. Отсюда  . В то же время при
. В то же время при  плотность пара
плотность пара  . Следовательно,
. Следовательно,  , и в результате
, и в результате
 ;
; 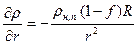 . (7)
. (7)
Подставляя это значение градиента плотности в (1), получаем:
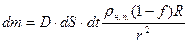 . (8)
. (8)
Если условия опыта стационарны, то масса паров, диффундировавших за время dt через полусферическую поверхность с радиусом r, равна:
 . (9)
. (9)
В то же время при уменьшении радиуса полусферической капли от R до (R-dR) изменение её массы dmк будет равно:
 , (10)
, (10)
где rж – плотность жидкости.
Учитывая, что убыль массы капли равна массе диффундировавшего пара: 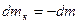 , с помощью уравнений (9) и (10) можно связать коэффициент диффузии D со скоростью изменения радиуса капли R:
, с помощью уравнений (9) и (10) можно связать коэффициент диффузии D со скоростью изменения радиуса капли R:
 . (11)
. (11)
В данной работе будет измеряться не радиус, а масса испаряющейся полусферической капли в зависимости от времени. Выразим радиус капли через ее массу  (в дальнейшем для краткости мы опускаем индекс «к» у массы капли):
(в дальнейшем для краткости мы опускаем индекс «к» у массы капли): 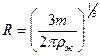 . Как видно из (10),
. Как видно из (10), 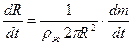 . Поэтому формула (11) может быть преобразована к виду:
. Поэтому формула (11) может быть преобразована к виду:
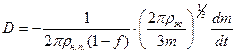 .
.
Учитывая, что 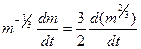 , получим:
, получим:
 ,
,
или  . (12)
. (12)
Из полученного выражения ясно, что для экспериментального определения D необходимо измерить изменение массы капли со временем при стационарных условиях.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Экспериментальная установка состоит из электронных аналитических весов, измеряющих вес капли с точностью до 0,1 мг, и подложки из фторопласта, на которую из шприца выдавливается капля исследуемой жидкости. При испарении капли показания весов непрерывно изменяются. Отсчет времени производится по секундомеру. Температура воздуха и его относительная влажность измеряются с помощью психрометра.