Задачи векторной оптимизации

Лабораторная работа

Тема:Многокритериальные задачи принятия решений в условиях определенности

Задачи векторной оптимизации

 

В жизни целенаправленная деятельность человека устроена так, что приходится учитывать не одну, а сразу несколько целей. Так, при транспортировке грузов возникают желания организовать перевозку быстро, дешево, надежно. Три сформулированные целевые установки приводят по отдельности к различным трем решениям, а так как цели сами по себе противоречивы, то возникают определенные трудности сравнения этих решений, выбора наилучшего в определенном смысле или какого-то компромиссного. В данном разделе рассмотрим подходы количественного обоснования решения многокритериальных задач оптимизации.

Вернемся к задаче определения плана выпуска продукции, рассмотренной в первой части пособия. Напомним постановку задачи.

Пусть мебельная фабрика изготавливает два вида продуктов: столы и шкафы. Для их производства используется три вида ресурсов (пиломатериал, шурупы, краска). Будем считать, что месячные запасы ресурсов ограничены: пиломатериал — величиной 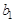(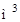), шурупы — 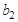(кг), краска — 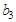(кг). Расходы соответствующих ресурсов на изготовление одной единицы соответствующих продуктов известны и задаются таблицей (матрицей) 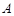. Прибыль (доход) от выпуска единицы соответствующей продукции задана: для стола она равна 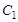(руб./шт.), для шкафа — 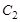(руб./шт.). Требуется определить план выпуска продукции каждого вида, максимизирующий доход фабрики.

Кроме этой цели, добавим еще одну. Допустим, что нам нужно максимизировать выпуск продукта первого типа — столов, которые идут не на продажу, а для своих нужд. Таким образом, теперь модель задачи будет выглядить так:

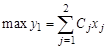— критерий первого вида; (2.1)

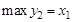— критерий второго вида; (2.2)

при ограничениях:

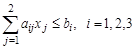, (2.3)

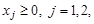(2.4)

где 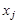— количество производимых продуктов j- го типа (соответственно столов и шкафов), j = 1,2;

— нормативная матрица затрат i -го вида сырья на 1 единицу j -го типа продукта;

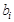— ограничение на i -й вид сырья (пиломатериал, шурупы, краска), j = 1,2,3.

Вернемся к графическому способу решения задачи в отдельности по каждому из критериев (рис. 2.1).

 

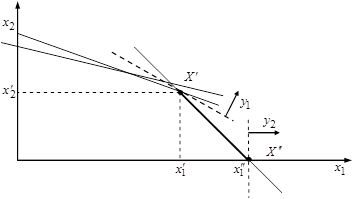
Рис. 2.1 — Графическое решение задачи

 

Если решать задачу только с учетом критерия первого вида 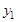, то решение получим в точке 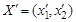= (517,156), а значение критерия 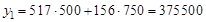рублей. Если решать задачу без учета критерия первого вида, а только с учетом критерия второго вида, то получим решение в точке 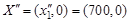, а значение критерия 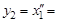700 столов.

Одновременный учет двух критериев приведет к решению, которое лежит на отрезке между точками (решениям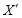и) и 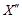. Множество решений на отрезке между 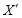и 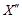называют множеством решений, оптимальных по Парето (оно же компромиссное множество, недоминируемое, эффективное). Множество компромиссных решений обладает свойством противоречивости: улучшение качества решений по одним критериям вызывает ухудшение качества других (рис. 2.2).

 

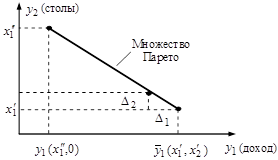
Рис. 2.2 — Компромиссное множество решений

 

Вообще говоря, в многокритериальных задачах принятия решений понятие оптимальности плана теряется, так как не существует такого плана, который доставлял бы одновременно экстремальное значение отдельным критериям. Это обстоятель­ство и является причиной того, что методы решения много­критериальных задач предусматривают в том или ином виде учет мнения лица, принимающего решение. Чтобы выбрать из области Парето лучшие решения, ЛПР обязан ввести соответствующие принципы выбора компромиссного решения, приводящие к тому или иному методу решения задачи. Рассмотрим наиболее часто употребляемые методы решения многокритериальных задач.

 

 

Сведение многокритериальной задачи к однокритериальной

Идея метода состоит в том, чтобы два и более критериев представить в виде единого суперкритерия, т.е. скалярной функции, зависящей от локальных критериев:

.

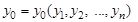Вид функции 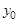определяется тем, как ЛПР представляет вклад каждого критерия 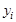в суперкритерий. В силу того, что критерии 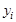могут измеряться в различных единицах измерения и иметь различные несоизмеримые масштабы, сравнивать решения в таких условиях зачастую невозможно. Возникает проблема приведения их масштабов к единому, обычно безразмерному масштабу измерения (проблема нормализации). А так как обычно локальные критерии имеют относительно друг друга различную важность, относительный вклад в суперкритерий, то это следует учитывать при выборе лучшего решения (проблема учета приоритета критериев).

Наибольшее распространение получил подход определения глобального критерия (суперкритерия) в виде взвешенной суммы критериев

,

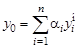где 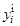— отнормированное значение i -го критерия;

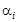— коэффициент относительной важности i-го критерия (весовой коэффициент);

.

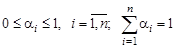Весовой коэффициент определяется экспертными методами. Значение 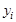для каждого из критериев, как правило, есть безразмерная величина и находится в интервале 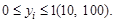Наиболее простым способом нормализации [7] является получение оценок по формул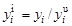е , где 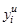— идеальное (возможно максимальное) значение i -го критерия.

Для решения нашей двухкритериальной задачи ЛПР должен установить значения весовых коэффициентов 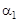и 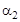, чтобы 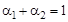, а также учесть нормализацию критериев 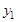и , а затем построить единую целевую функцию и решить задачу: 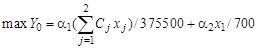, при ограничениях ; .

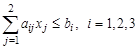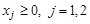Если 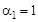, то получим решение с учетом первого критерия, если 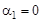— решение с учетом второго критерия. Глубокое знание реальной проблемы, накопленный опыт могут позволить ЛПР выбрать 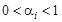, чтобы, решив оптимизационную задачу с единственной целевой функцией 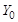, он получил бы удовлетворяющее его решение исходной задачи с двумя целевыми функциями.

Выделение главного критерия

Допустим, что среди критериев 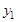и ЛПР удается выбрать основной. Пусть это будет критерий 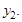Допустим, что ЛПР желает получить доход от реализации продукции не ниже определенной им величины 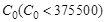. Тогда можно решать задачу вида: 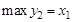, при ограничениях:

;

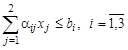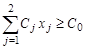— ограничение по критерию ;

.

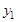Метод последовательных уступок

Предположим, что частные критерии упорядочены в порядке убывания их важности 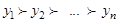. Решая задачу по критерию 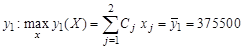, найдем решение 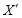. Если ЛПР может сделать некоторую уступку по первому критерию 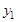в объеме 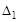(пусть 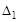= 5500), чтобы улучшить решение по следующему критерию (рис. 3.32), то это приводит к задаче поиска решения по второму критерию с уступкой по первому: 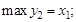при ограничениях:

;

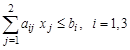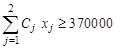— уступка по первому критерию;

.

И так далее для других критериев. На последнем шаге решается задача поиска решения по n -му критерию с учетом уступок по 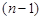наиболее важным критериям, и решение этой задачи принимается в качестве решения первоначальной.

Метод целевой точки

Метод целевой точки (опорной, идеальной) базируется на задании по каждому критерию так называемых уровней притязаний [3, 4,7] в виде желаемых значений критериев 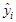. Поскольку оценки 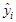задаются без точного знания структуры множества допустимых решений, то целевая точка может оказаться как внутри, так и вне области допустимых решений. Наиболее близкая точка решения к целевой будет определять наилучшее решение. В качестве меры близости между решением и целевой точкой, т.е. между векторами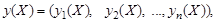 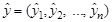предлагается использовать различные расстояния [4], в том числе расстояние типа

,

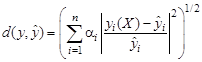где 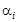— коэффициент относительной важности критерия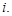

Тогда модель поиска компромиссного решения для рассматриваемой задачи методом целевой точки будет иметь вид

,

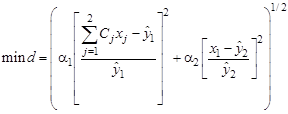при ограничениях (3.52) и (3.53).

На базе рассмотренных методов поиска решения многокритериальных задач созданы различные человеко-машинные эвристические процедуры [28], суть которых заключается в распределении ролей между ЛПР и ЭВМ. ЛПР готовит информацию, необходимую для моделирования, ЭВМ осуществляет расчет и выдает решение ЛПР для его анализа. При необходимости ЛПР сообщает сведения для корректировки решения в виде оценок относительной важности критериев, уступок по критериям, коэффициентов нормализации и другие.

Варианты для многокритериальной ЗПР

1.

Для приготовления комбикорма совхоз может закупить зерно 4-х сортов Ki, отличающихся друг от друга содержанием питательных компонентов Cj (j=1,..,5).Для обеспечения нормального питания скота в течение планируемого периода комбикорм должен содержать не менее Bj питательного компонента j-го типа. Одна тонна зерна i-го типа стоит ri рублей и содержит aij единиц питательного компонента j-го типа (табл.4.3). Складские помещения позволяют хранить не более А тонн зерна (для варианта 5: А=2800, для варианта 6: А=4400). Определить план закупки зерна, чтобы обеспечить максимальную питательность комбикорма при минимальных затратах с учетом емкости складских помещений.

 

Исходные данные к задаче Таблица1.

Сорт зерна Ki	С1	С2	С3	С4	С5	Цена ri
К1				0.6	0.01
К2				0.25	0.02
К3				1.00	0.1
К4				1.5	0.5
К5				0.5	0.1
Содержание Bj

 

Вариант 1: к1, к2, к3

Вариант 2: к2, к3, к4

Вариант 3: к3, к4, к5

Вариант 4: к4, к5, к1

 

2.

Совхоз, имеющий посевную площадь 5000 га, выращивает3 культуры Кi. Весь год можно разбить на 5 периодов Pj, отличающихся друг от друга потребностями в рабочей силе для выполнения сельскохозяйственных работ. В период Pj совхоз располагает рабочей силой в количестве bj человек, из которых dj человек могут быть в случае необходимости обеспечены работой, не связанной непосредственно с сельским хозяйством, а aij человек должны быть заняты на обработке 1 га посевной площади, занятой культурой Ki. Прибыль от i-й культуры, приходящаяся на 1 га посевной площади, равна ci рублей, плановое задание по производству i-й культуры составляет qi центнеров, а ее урожайность hi центнеров с га (табл.2).

Найти распределение площади под эти культуры, обеспечивающее максимум прибыли при выполнении всех плановых заданий и полной загрузке рабочей силы в течение года.

 

 

Исходные данные к задаче 2 Таблица 2.

Культура	P1	P2	P3	P4	P5	ci	qi	hi
K1	0.25			1.4	1.3
K2	0.2	1.8		0.8	0.6
К3	0.2	0.2	0.4	1.3
К4	0.1	0.5		1.8	0.4
bj
dj

 

Вариант 5: к1, к2, к3

Вариант 6: к2, к3, к4

Вариант 7: к4, к1, к2

Вариант 8: к3, к1, к4

 

3.

Деревообрабатывающая фабрика получает m типов лесоматериалов Hi в количестве bi куб.м в месяц. Из этих материалов изготавливается n ви

дов фанеры Sj. На производство 1 кв.м фанеры вида Sj идет qij куб.м

материала Hi. По плану в месяц должно производится не менее Pj кв.м

фанеры вида Sj. Составить план производства фанеры на месяц, обеспечивающий фабрике максимальную прибыль, если лесоматериалы обходятся фабрике в ci руб./куб.м, расходы на производство 1 кв.м фанеры Sj составляют vj рублей, а реализуется эта фанера по цене rj руб./кв.м.

 

 

Исходные данные к задаче 3 Таблица 3.

Тип	S1	S2	S3	S4	S5	bi	ci
H1	0.02		0.03	0.08	0.02		2.6
H2	0.04	0.1	0.12		0.01		2.5
H3		0.05	0.02	0.04	0.04		1.5
H4	0.1	0.04			0.08		1.4
H5	0.02		0.01				1.9
Pj
vj	0.5	0.7	0.4	0.8	0.9
rj		3.5	4.1	3.2	4.5

 

Вариант 9: h1, h2, h3

Вариант 10: h2, h3, h4

Вариант 11: h3, h4, h5

Вариант12: h4, h5, h1

Вариант 13: h2, h4, h5

Вариант14: h3, h5, h1