Задание на курсовую работу
В курсовой работе требуется формализовать поставленную задачу, разработать эффективные алгоритмы решения, реализовать алгоритм в виде программы, исследовать и оценить теоретически и экспериментально временную и емкостную сложность алгоритмов.
В качестве задачи на курсовую работу была предложена следующая комбинаторная задача:
Задаются арифметические операции, в которых цифры заменены буквами. В данной операции одна и та же буква всегда заменяет одну и ту же цифру, разные буквы представляют разные цифры. Число разрядов исходных чисел (не результат операции) - не более N. Восстановить все возможные значения букв и операций.
Исследовать асимптотическую временную сложность решения задачи в зависимости от N.
Пример: SEND MORE MONEY соответствует 9567+1085=10652.
При выполнении курсовой работы требуется:
· Формализовать поставленную задачу (перейти от словесной неформальной постановки к математической формулировке);
· Приспособить общие методы и алгоритмы решения к решению конкретной задачи;
· Провести сравнительную оценку различных вариантов с целью выбора наиболее эффективных структур данных и алгоритмов обработки;
· Исследовать и оценить теоретические и экспериментальные методы сокращения перебора в комбинаторных задачах;
· Оценить аналитически и экспериментально эффективность предложенных в работе алгоритмов (временную и емкостную сложности);
· Программно реализовать разработанные алгоритмы на одном из алгоритмических языков программирования.
· Экспериментально исследовать различные способы программной реализации алгоритмов.
Анализ задания. Выводы о методах решения и путях повышения эффективности вычислений
|
|
математический алгоритм программирование данные
Рассмотрим индивидуальное задание и проанализируем методы решения. Эта задача имеет логическое ограничение на количество различных букв в строке - количество цифр 10. Поэтому, бесконечно расти, эта задача может только в размерности чисел, но здесь ограничение может быть наложено скорее возможностями программных средств, чем алгоритмом реализации.
Сама идея решения данной задачи заключается в том, что мы последовательно проходим введенную строку и заменяем все вхождения одной буквы на выбранную цифру. После расстановки цифр расставляются знаки операции, и проводится проверка (является решением или нет). Знаков операции всего 4: сложение, вычитание, умножение и деление. Знак ‘=’ ставится вместо последнего не буквенного символа. Так как выбор цифр, которые будут подставлены, выбираются последовательно необходимо запретить выбор тех же цифр. Для этого создадим таблицу размером 10×10, и введем следующие обозначения
0- символ можно выбрать:
1- символ выбран в этой строчке в настоящее время;
- символ был использован в этой строчке раньше (в этой строчке использовать этот символ больше нельзя, но в следующих можно);
- символ выбран в выше стоящей строчке;
Ввод данной таблицы обусловлен тем, что в данной задаче не возможно определить для данного узла какие значения уже подставлялись, а какие нет. В этом случае возможно повторная проверка уже пройденного пути.
I.
Формализация задачи
Структуры данных для представления объектов задачи
|
|
Основная работа в алгоритме решения данной задачи происходит с исходной строкой и лишь на конечном этапе производится перевод чисел записанных в строке в числовую форму.
Для алгоритма поиска с возвращением обычно решением является вектор(a1, a2,…), но в нашем случае таким решением будет строка с полностью замененными буквами и подставленными знаками, которая и выводится на экран, в том случае если она верна.
Выбор следующего шага выполняется по таблице описанной выше. Так же выполняется подстановка знаков. При продвижении в глубину в строке проставляются 3 в тех столбцах, где в предыдущей строке стоит 3 или 1, и эти цифры уже не могут быть выбраны.
Анализ ограничений и усовершенствований. Аналитические и/или экспериментальные оценки
Основное ограничение в этой задаче указано в самом задании. Это ограничение связано в однозначном соответствии букв и цифр.
Второе ограничение накладывается на количество знаков, оно влияет на количество пройденных вершин и соответственно на время работы алгоритма. В данной работе это ограничение равно 4. Максимальное число узлов дерева равно 10!. И рассчитывается по формуле:
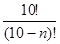, где n - число различных букв в строке.