Линейная зависимость и независимость системы векторов.
Определение. Пусть 
- скаляры, 
- векторы. Линейной комбинацией векторов с коэффициентами 
называется вектор:
(2.1)
Пример. Для векторов 
; 
вычислить линейную комбинацию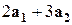 
.
.
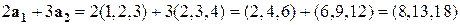Определение. Система векторов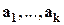 
называется линейно независимой тогда и только тогда, когда для любых скаляров из равенства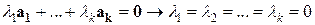 
.
Другими словами, система векторов 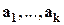линейно независима тогда и только тогда, когда из равенства линейной комбинации этих векторов нулевому вектору, следует, что все коэффициенты равны числу нуль.
Определение. Система векторов 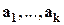называется линейно зависимой тогда и только тогда, когда существуют 
, такие, что (
) (2.2)
и не все скаляры равны нулю.
Другими словами, система векторов 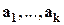линейно зависима тогда и только тогда, когда существуют скаляры не все равные нулю, такие, что линейная комбинация векторов с этими коэффициентами равна нулевому вектору.
Из определения следуют два утверждения.
1) Если система векторов 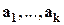не является линейно независимой, то она линейно зависима, и наоборот.
Доказательство.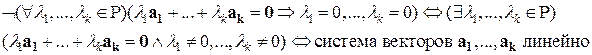 
зависима.
■
2) Система векторов - линейно зависима тогда и только тогда, когда уравнение 
имеет ненулевое решение, то есть 
.
Пример 1. Будет ли система векторов 
из 
линейно зависима или линейно независима?
векторы 
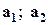линейно независимы.
Пример 2. Рассмотрим векторы:
Система векторов 
называется системой единичных векторов векторного пространства. Докажем, что эта система векторов линейно независима.
система векторов 
- линейно независима.
Замечание.
1) На плоскости единичными векторами являются векторы:
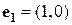= i, 
= j.
2) В трёхмерном пространстве единичными векторами являются векторы:
|
|
= i, 
= j, 
= k.
Теорема 2.1. ( Критерий линейной зависимости).
Система векторов 
, где 
, линейно зависима тогда и только тогда, когда один из векторов этой системы является линейной комбинацией предшествующих векторов.
Другими словами. Для того чтобы векторы , где 
, были линейно зависимы, необходимо и достаточно, чтобы один из них являлся линейной комбинацией остальных.
Доказательство.
Необходимость. Пусть 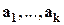линейно зависимая система векторов, тогда существуют 
, такие, что 
и не все 
. Пусть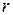 
- наибольший индекс, такой, что скаляр 
. Тогда из 
следует, что 
значит 
. Получили, что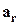 
- линейная комбинация предшествующих векторов.
Достаточность. Пусть 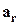- линейная комбинация векторов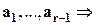 
. Выпишем коэффициенты: 
- не все 
, поэтому система векторов линейно зависима.
Теорема доказана.
Геометрическая интерпретация линейной зависимости сформулирована в теореме 2.2 и теореме 2.3.
Теорема 2.2. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Теорема 2.3. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Теорема 2.4. Любые четыре вектора линейно зависимы.
Доказательство этих теорем – самостоятельно (см. стр. 10-11 лекции 2 (Крищенко А.П., Канатников).
Теорема 2.2. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство.
