Геометрический смысл векторного произведения.
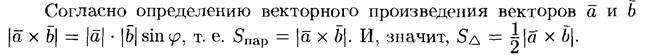
Другими словами, модуль векторного произведения векторов а, b численно равен площади параллелограмма, построенного на векторах а, b.
Площадь треугольника, построенного на векторах а, b, равна половине модуля векторного произведения этих векторов.
Механический смысл векторного произведения.
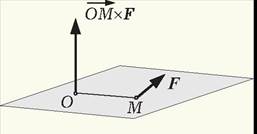
Если вектор b является силой, приложенной к точке А, вектор а направлен из точки О в точку А, то векторное произведение векторов а, b равно моменту силы b относительно точки О.
Свойства векторного произведения.
1°. Для того чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нуль-вектору.
◄ Необходимость. Если векторы коллинеарны, то их векторное произведение равно нуль- вектору согласно определению. Докажем достаточность. Если a х b = 0, то | a x b | = 0, т.е. | a | | b | sin р = 0, где р — угол между векторами а и b. Но тогда выполнено, по крайней мере, одно из трех равенств: | а | = 0, | b | = 0 или sin р = 0. Каждое из этих равенств влечет коллинеарность векторов а и b. ►
Следующее свойство выражает геометрический смысл модуля векторного произведения.
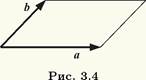
2°. Если векторы а и b неколлинеарны, то модуль | а х b | их векторного произведения равен площади параллелограмма, построенного на этих векторах как на смежных сторонах (рис. 3.4).
|
◄ Свойство объясняется тем, что модуль векторного произведения и площадь параллелограмма по двум смежным сторонам и углу между ними вычисляют по одной и той же формуле как произведение длин векторов (сторон параллелограмма) на синус угла между ними. ►
3°. Важнейшими свойствами векторного произведения являются следующие три:
- свойство антикоммутативности a x b = - b x a;
- свойство ассоциативности совместно с умножением на число
- ( a)x b =
a)x b =  (a x b);
(a x b);
- свойство дистрибутивности относительно сложения:
(а + b)x c = a x c + b x c – правый дистрибутивный закон,
c x (а + b) = c x a + c x b –левый дистрибутивный закон.
Доказывая свойство антикоммутативности, заметим, что если векторы а и b коллинеарны, то в обеих частях равенства a x b = - b x a в соответствии со свойством 1° стоит нулевой вектор. Если же векторы а и b неколлинеарны, то существует плоскость, которой они параллельны. В силу первого условия определения векторного произведения векторы a x b и b x a перпендикулярны этой плоскости и, следовательно, коллинеарны. Ясно, что и длины векторов a x b и b x a равны, поскольку совпадают с площадью одного и того же параллелограмма (свойство 2°). Остается доказать, что векторы a x b и b x a имеют противоположное направление. Это следует из того, что если тройка векторов а, b, a x b правая, то тройка b, а, a x b — левая. Поэтому, заменив в последней тройке третий вектор на противоположный, получим правую тройку векторов b, а, -a x b, причем вектор — a x b коллинеарен вектору b x a и имеет ту же длину. Согласно определению, это означает, что вектор - a x b равен векторному произведению векторов b и
а, т.е. a x b =- b x a.
Свойство ассоциативности доказывается аналогично. В случае коллинеарных векторов а и b также при  = 0 векторы (
= 0 векторы ( a)x b и
a)x b и  (a x b) равны нуль-вектору, поскольку каждый из них является или векторным произведением коллинеарных векторов, или произведением вектора на число, равное нулю. Следовательно, в рассматриваемых случаях равенство (
(a x b) равны нуль-вектору, поскольку каждый из них является или векторным произведением коллинеарных векторов, или произведением вектора на число, равное нулю. Следовательно, в рассматриваемых случаях равенство ( a)x b =
a)x b =  (a x b) выполнено.
(a x b) выполнено.
Предположим теперь, что векторы a и b неколлинеарны, а  = 0. Покажем сначала, что в левой и правой частях доказываемого равенства стоят коллинеарные векторы, равные по длине. Действительно, если считать, что векторы a, b и
= 0. Покажем сначала, что в левой и правой частях доказываемого равенства стоят коллинеарные векторы, равные по длине. Действительно, если считать, что векторы a, b и  a имеют общее начало, то пары a, b и
a имеют общее начало, то пары a, b и  a, b неколлинеарных векторов порождают одну и ту же плоскость, которой перпендикулярны их векторные произведения a x b и (
a, b неколлинеарных векторов порождают одну и ту же плоскость, которой перпендикулярны их векторные произведения a x b и ( a)x b. Поэтому векторы
a)x b. Поэтому векторы  (a x b) и (
(a x b) и ( a)x b коллинеарны. Вычисляя их длины, убеждаемся, что эти длины равны, так как
a)x b коллинеарны. Вычисляя их длины, убеждаемся, что эти длины равны, так как
|  (a x b)| = |
(a x b)| = |  | | a x b | = |
| | a x b | = |  | | a | | b | sin
| | a | | b | sin 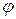 ,
,
где 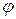 — угол между векторами a и b,
— угол между векторами a и b,
|( a)x b | = |
a)x b | = |  a | | b | sin
a | | b | sin 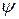 = |
= |  | | a | | b | sin
| | a | | b | sin 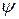 = |
= | 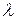 | | a | | b | sin
| | a | | b | sin 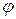 ,
,
где 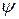 — угол между векторами
— угол между векторами  a и b и использовано равенство sin
a и b и использовано равенство sin 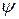 = sin
= sin 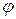 , выполненное при всех
, выполненное при всех 
 0.
0.
Два коллинеарных вектора, равные по длине, либо совпадают, либо являются противоположными друг другу. Нам достаточно исключить последнюю возможность, доказав, что векторы ( a)x b и
a)x b и 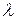 (a x b) являются однонаправленными.
(a x b) являются однонаправленными.
Если  > 0, то векторы a и
> 0, то векторы a и  a однонаправлены. Следовательно, векторы (
a однонаправлены. Следовательно, векторы (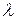 a)x b и a x b тоже являются однонаправленными. А поскольку векторы a x b,
a)x b и a x b тоже являются однонаправленными. А поскольку векторы a x b,
 (axb) тоже однонаправлены, то однонаправлены и векторы (
(axb) тоже однонаправлены, то однонаправлены и векторы (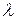 a)x b и
a)x b и
 (axb).
(axb).
Если  < 0, то векторы a и
< 0, то векторы a и  a являются противоположно направленными. Следовательно, векторы (
a являются противоположно направленными. Следовательно, векторы ( a)x b и a x b тоже являются противоположно направленными. Умножение вектора a x b на отрицательное число
a)x b и a x b тоже являются противоположно направленными. Умножение вектора a x b на отрицательное число 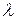 меняет его направление на противоположное. Поэтому векторы (
меняет его направление на противоположное. Поэтому векторы ( a)x b и
a)x b и 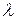 (a x b) имеют одинаковое направление.
(a x b) имеют одинаковое направление.
Доказательство свойства дистрибутивности будет дано позже (см. 3.2).
Замечание 3.1. Доказанные свойства ассоциативности и дистрибутивности векторного произведения объединяют, аналогично случаю скалярного произведения, в свойство линейности векторного произведения относительно первого сомножителя. В силу свойства антикоммутативности векторного произведения векторное произведение линейно и относительно второго сомножителя:
a x( b) = -(
b) = -( b)x a = -
b)x a = -  (b x a) =
(b x a) =  (a x b),
(a x b),
a x(b + c) = - (b + c)x a = -(b x a + c x a) = a x b + a x c.
Пример 3.1. Найти площадь S треугольника, построенного на векторах
a = 3 c -2 d и b = c + d при условии, что | c | = 1, | d | = 4, а угол 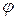 между векторами c и d равен 30°.
между векторами c и d равен 30°.
Решение. Для решения задачи воспользуемся формулой
S = 0,5 | a x b |.
Используя алгебраические свойства векторного произведения, находим, что
a x b = (3 c -2 d)x (c + d) = 3 c x c + 3 c x d — 2 d x c — 2 d x d = 3 c x d + +2 c x d = 5 c x d. Поэтому
◄ S = 0,5 | a x b | = 0,5 |5 c x d | = 2,5 | c | | d | sin 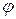 = 5.
= 5.
◄