Тема: Использование WolframAlpha при решении математических задач
Литература.
А.С. Маренич, Е.Е. Маренич. Использование WolframAlpha при решении математических задач.-М.: МГТУ им. Н.Э.Баумана, 2016. Издание доступно в электронном виде на портале ebooks.bmstu.ru по адресу: https:// ebooks.bmstu.ru/catalog/109/book1533.html
Замечание. Адрес WolframAlpha: https://www.wolframalpha.com/
Разберём на примерах некоторые элементы синтаксиса.
Порядок выполнения математических операций в запросе определяется скобками. Для того чтобы попасть в справочник по синтаксису запросов нужно нажать кнопку 
.
Операции над действительными (комплексными) числами. Мнимая единица 
: . Операция сложения 
: . Операция вычитания 
: . Операция умножения 
: 
или . Операция деления 
: 
. Операция возведения в степень 
: 
.
Пример. Вычислить: 
Составляем запрос.
Ответ: Результат вычисления равен:
Упрощение выражений.
Упростить выражение 
: 
или 
■
Пример 1. Упростить дробь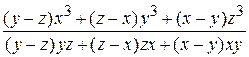 
.Составляем запрос на упрощение:
Если нажать на кнопку “Step-by-step solution”, то получим пошаговое решение или комментарий к решению
Результат упрощения: 
. ■
Функции действительного (комплексного) переменного.
Квадратный корень 
: 
.
Степень 
: 
. Экспоненциальная функция 
: 
или 
. Логарифм по основанию 
, 
: 
. Натуральный логарифм 
: 
. Косинус 
: 
. Синус 
: 
. Тангенс 
: 
.
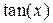Котангенс 
: 
. Секанс 
: 
. Косеканс 
: 
.
Сервис 
при работе с функцией 
использует обозначение 
. Аналогичные обозначения применяются и к другим обратным тригонометрическим функциям.
Арккосинус 
: 
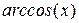или 
. Арксинус 
: 
или 
. Арктангенс 
: 
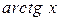или 
. Арккотангенс 
: 
или 
.
Гиперболический косинус, 
. Гиперболический синус, 
. Гиперболический тангенс, 
. Гиперболический котангенс, 
.
Вычисление значений функции 
в точках 
:
.
Область определения функции 
одной или нескольких переменных: 
.
Множество значений функции одной или нескольких переменных: 
.
Четность и нечетность функции одной или нескольких переменных: 
, или 
, или
Область определения и множество значений функции одной или нескольких переменных: 
.
Инъективность функции одной переменной:
Сюръективность функции одной переменной: 
Непрерывность функции одной переменной: 
Точки, в которых функция одной переменной не является непрерывной: 
.
Вычисление периода функции одной или нескольких переменных:
.
Задача 1. Исследовать свойства функции , значения которой заданы формулой: 
.
1) Найдем область определения и множество значений функции .
Составляем запрос.
Отметим область определения и множество значений функции на числовой оси:
2) Найдем точки пересечения графика с осями.
Так как точка 
не принадлежит области определения функции , то график не пересекается с осью 
.Точка пересечения графика с осью 
находится из уравнения 
:
Составляем запрос.
Точка пересечения графика с осью 
изображена на рисунке:
Производная 
:
или 
, или 
.
Пример. Вычислить первую и вторую производные функции.
1) 
Составляем запрос.
Ответ: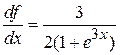 
Составляем запрос:
Ответ: 
Замечание. Можно сразу делать запрос на вычисление производной второго порядка, не вычисляя первую производную,....
Вторая производная 
: 
.
Производная 
порядка 
: 
.