Оглавление
Введение
Предикаты: определения и примеры
Заключение
Список используемых источников
Введение
В чемсостоит необходимость введения предикатов в математику?
Дело в том, что сама по себе логика высказываний обладает довольно слабыми выразительными возможностями. Пользуясь только логикой, нельзя выразить даже очень простые, с математической точки зрения, рассуждения.
Возьмем, например, следующее умозаключение. "Всякое целое число является рациональным. Число 5 - целое. Следовательно, 5 - рациональное число". Все эти три утверждения с точки зрения логики высказываний являются атомарными. Т.е. только средствами логики высказываний нельзя вскрыть внутреннюю структуру и поэтому нельзя доказать логичность этого рассуждения в рамках логики высказываний. Средства, предоставляемые логикой высказываний, оказываются недостаточными для анализа многих математических рассуждений. В алгебре логики не рассматриваются ни структура высказываний, ни тем более, их содержание. В то же время и в науке, и в практике используются заключения, существенным образом зависящие как от структуры, так и от содержания используемых в них высказываний.
Например, в рассуждении " Всякий ромб - параллелограмм; ABCD - ромб; следовательно, ABCD - параллелограмм" посылки и заключение являются элементарными высказываниями логики высказываний, и с точки зрения этой логики рассматриваются как целые, неделимые, без учёта их внутренней структуры. Следовательно, алгебра логики, будучи важной частью логики, оказывается недостаточной в анализе многих рассуждений.
Поэтому возникает необходимость в расширении логики высказываний и построении такой логической системы, средствами которой можно исследовать структуру и содержание тех высказываний, которые в логике высказываний рассматриваются как элементарные.
В силу изложенного материала, можно заключить, что актуальность данной работы несомненна.
Цель данного реферата заключается в том, чтобы совершить обзор
литературных источников по проблеме предикатов в дискретной математике.
Для достижения поставленной цели необходимо решить следующие задачи:
· найти нужную информацию о предикатах по данной теме;
· тщательно проанализировать и выбрать нужные данные;
· оформить реферат согласно требованиям.
Объектом исследования является архив материалов по математическим предикатам.
Предметом исследования являются предикаты в дискретной математике.
Реферат состоит из введения, основной части, заключения и списка использованной литературы.
Предикаты: определения и примеры
Введем основное понятие темы.
Определение 1. Пусть М - непустое множество. Тогда n-местным предикатом, заданным на М, называется выражение, содержащее n переменных и обращающееся в высказывание при замене этих переменных элементами множества М [1].
Поясним конкретными примерами. Пусть М есть множество натуральных чисел N. Тогда, например, такие выражения: "x - простое число", "x - четное число", "x больше 10" являются одноместными предикатами. При подстановке вместо x произвольных натуральных чисел получаются высказывания: "2 - простое число", "6 - простое число", "3 - четное число", "5 больше 10" и т.д. [2]
Множество M, на котором задан предикат, называется областью определения предиката [3].
Множество 
, на котором предикат принимает только истинные значения, называется областью истинности предиката Р (х) [3].
Так, предикат P (x) - " х - простое число" определён на множестве N, а множество 
для него есть множество всех простых чисел.
Вот такие выражения: " x больше y", " x делит y нацело", " x плюс y равно 10, или x+y=10 " являются двухместными предикатами. Примеры трехместных предикатов, заданных на множестве натуральных чисел: " число z лежит между x и y", " x плюс y равно z", " |x-y| = z " [4].
Обычно полагают, что, если имеется такой предикат, в котором нет переменных для замены, то подобное высказывание - нульместный предикат [1].
Причем местность предикатов не всегда равна числу всех переменных, содержащихся в выражении.
Например, выражение " существует число x такое, что y = 2 x " на множестве натуральных чисел определяет одноместный предикат.,
По смыслу этого выражения, в нем можно заменять только переменную y. Например: если применить замену y на 6, то получим истинное высказывание: " существует число x такое, что 6 = 2x", а если заменим y на 7, то получим ложное (на множестве N) высказывание: " существует число x такое, что 7 =2x".
Предикат с заменяемыми переменными x1,…,xn обычно обозначается заглавной латинской буквой, после которой в скобках указываются эти переменные. Например, P (x1,x2), Q (x2,x3), R (x1). Среди переменных в скобках могут быть и фиктивные [2].
Определение 2. Предикат (n -местный, или n -арный <https://ru.math.wikia.com/wiki/%D0%90%D1%80%D0%BD%D0%BE%D1%81%D1%82%D1%8C>) - это функция <https://ru.math.wikia.com/wiki/%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)> с областью значений 
(или " Истина " и " Ложь "), определённая на n -й декартовой степени <https://ru.math.wikia.com/wiki/%D0%9F%D1%80%D1%8F%D0%BC%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%B5%D0%B4%D0%B5%D0%BD%D0%B8%D0%B5> множества <https://ru.math.wikia.com/wiki/%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE> M. Таким образом, каждую n -ку элементов M предикат характеризует либо как "истинную", либо как "ложную" [5].
Предикат можно связать с математическим отношением <https://ru.math.wikia.com/wiki/%D0%9E%D1%82%D0%BD%D0%BE%D1%88%D0%B5%D0%BD%D0%B8%D0%B5_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)>: если n -ка принадлежит отношению, то предикат будет возвращать на ней 1 [3].
Предикат - один из элементов логики первого <https://ru.math.wikia.com/wiki/%D0%9B%D0%BE%D0%B3%D0%B8%D0%BA%D0%B0_%D0%BF%D0%B5%D1%80%D0%B2%D0%BE%D0%B3%D0%BE_%D0%BF%D0%BE%D1%80%D1%8F%D0%B4%D0%BA%D0%B0> и высших порядков <https://ru.math.wikia.com/wiki/%D0%9B%D0%BE%D0%B3%D0%B8%D0%BA%D0%B0_%D0%B2%D1%8B%D1%81%D1%88%D0%B8%D1%85_%D0%BF%D0%BE%D1%80%D1%8F%D0%B4%D0%BA%D0%BE%D0%B2?action=edit&redlink=1>. Начиная с логики второго порядка <https://ru.math.wikia.com/wiki/%D0%9B%D0%BE%D0%B3%D0%B8%D0%BA%D0%B0_%D0%B2%D1%82%D0%BE%D1%80%D0%BE%D0%B3%D0%BE_%D0%BF%D0%BE%D1%80%D1%8F%D0%B4%D0%BA%D0%B0>, в формулах можно ставить кванторы <https://ru.math.wikia.com/wiki/%D0%9A%D0%B2%D0%B0%D0%BD%D1%82%D0%BE%D1%80> по предикатам [3].
Предикат называют тождественно - истинным [2] и пишут:
,
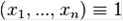если на любом наборе аргументов он принимает значение 1.
Предикат называют тождественно - ложным [2] и пишут:
,
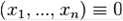если на любом наборе аргументов он принимает значение 0.
Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение 1 [5].
Например, обозначим предикатом EQ (x, y) отношение равенства (" x = y "), где x и y принадлежат множеству вещественных чисел <https://ru.math.wikia.com/wiki/%D0%92%D0%B5%D1%89%D0%B5%D1%81%D1%82%D0%B2%D0%B5%D0%BD%D0%BD%D0%BE%D0%B5_%D1%87%D0%B8%D1%81%D0%BB%D0%BE>. В этом случае предикат EQ будет принимать истинное значение для всех чисел, равных x и y.
Более житейским примером может служить предикат " ПРОЖИВАЕТ (x, y, z)" для отношения " x проживает в городе y на улице z " или предикат " ЛЮБИТ (x, y)" для выражения " x любит y", где множество M - это множество всех людей.
Так как предикаты принимают только два значения, то к ним применимы все операции булевой алгебры <https://ru.math.wikia.com/wiki/%D0%91%D1%83%D0%BB%D0%B5%D0%B2%D0%B0_%D0%B0%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0>, например: отрицание, импликация, конъюнкция, дизъюнкция и т.д. Итак, на совокупности всех предикатов, заданных на множестве М, вводятся знакомые логические операции: конъюнкция, дизъюнкция, отрицание, импликация и эквиваленция. Эти операции вводятся довольно очевидным образом. Приведем в качестве примера определение конъюнкции предикатов.
Определение 3. Предикат W (x1,…,xn) называется конъюнкцией предикатов U (x1,…,xn) и V (x1,…,xn), заданных на множестве М, если для любых а1,…, аn из М высказывание W (а1,…, аn) есть конъюнкция высказываний U (а1,…, аn) и V (а1,…, аn) [2].
Аналогично приводятся определения и других упомянутых выше операций.
В логике предикатов первого порядка вводятся и две новые операции. Называются они квантором общности и квантором существования [1]. Эти операции рассмотрим сначала на примерах.
Пусть дано выражение: " существует число х, такое, что x + y=10". На множестве натуральных чисел это предложение определяет одноместный предикат P (y), так, например, Р (2) и Р (9) - истинные высказывания, а Р (11) - ложное. Если обозначить предикат " x + y = 10 " через S (x,y) (а это предикат двухместный), то P (y) можно записать так: " существует х такой, что S (x,y)". В этом случае говорят, что предикат P (y) получен из предиката S (x,y) навешиванием квантора существования на x и пишут P (y) = (x) S (x,y)
Рассмотрим другой пример. Выражение " для всех х справедливо, что y = - х2 " определяет на множестве целых чисел одноместный предикат Q (y). Если предикат " y = - х2 " обозначить через T (x,y), то Q (y) можно записать так: "для всех x справедливо T (x,y)". В таком случае говорят, что предикат Q (y) получен из предиката T (x,y) навешиванием квантора общности на х и пишут Q (y) = (x) T (x,y).
Пользуясь этими примерами, дадим определение в общем виде.
Определение 4. Пусть P (x1,…,xn) - предикат, заданный на множестве M, y - переменная. Тогда выражение: " для всякого y выполняется P (x1,…,xn)" - предикат, полученный из P навешиванием квантора общности на переменную y, а выражение " существует y такой, что выполняется P (x1,…,xn)" - предикат, полученный из P навешиванием квантора существования на переменную y [1].
Заметим, что в определении не требуется, чтобы y была одна из переменных x1,…,xn, хотя в содержательных примерах, квантор навешивается на одну из переменных x1,…,xn. Указанное требование не накладывается, чтобы избежать усложнения определения формулы логики предикатов. Если y - одна из переменных x1,…,xn, то после навешивания квантора на y новый предикат является (n-1) - местным, если y 
{ x1,…,xn}, то местность нового предиката равна n [3].
Если предикат W (x1,…,xn) получен из предикатов U (x1,…,xn) и V (x1,…,xn) с помощью связок, то истинность высказывания W (a1,…,an) определяется таблицами истинности этих связок [3]. Пусть W (x1,…,xn) = (y) U (x1,…,xn,y). Тогда высказывание W (a1,…,an) истинно тогда и только тогда, когда для любого b 
M истинно высказывание U (a1,…,an,b). Если же W (x1,…,xn) = (y) U (x1,…,xn,y), то высказывание W (a1,…,an) истинно в том и только в том случае, когда найдется b 
M, для которого высказывание U (a1,…,an) истинно [4].
Вообще понятие предиката - весьма широкое понятие [1]. Это видно уже из приведенных выше римеров. Тем не менее, еще раз подчеркнем, показав, что n - местная функция может рассматриваться как (n+1) - местный предикат. Действительно, функции y = f (x1,…,xn), заданной на множестве М, можно поставить в соответствие выражение " y равно f (x1,…,xn)". Это выражение есть некоторый предикат P (x1,…,xn,y). При этом, если элемент b есть значение функции в точке (a1,…,an), то высказывание P (a1,…,an,b) истинно, и обратно. (Подобное "превращение" функции в предикат мы уже привели в качестве примера выше для сложения натуральных чисел.)
На предикаты можно взглянуть и более формально, причем с двух точек зрения.
Во-первых, предикат можно представить отношением следующим образом.
Пусть предикат P (x1,…,xn) задан на множестве M. Рассмотрим прямую степень этого множества Mn = Mx Mx…xM и подмножество Dp множества Mn, определяемое равенством:
Dp = { (a1,…,an) 
Mn 
высказывание P (a1,…,an) истинно}.
Отношение Dp можно назвать областью истинности предиката P. Во многих случаях предикат P можно отождествить с отношением Dp.
При этом, правда, возникают некоторые трудности при определении операций над отношениями, аналогичными операциям над предикатами [4].
Во-вторых, предикат P (x1,…,xn), заданный на M, можно отождествить с функцией fp: Mn {0,1}, определяемой равенством:
Говорят, что предикат Р (х) является следствием предиката Q (х) [5]: 
, если 
; и предикаты Р (х) и Q (х) равносильны:
,
Если
.
Приведём примеры к изложенному материалу.
Пример 1. Среди следующих предложений выделить предикаты и для каждого из них указать область истинности, если M = R для одноместных предикатов и M = R×R для двухместных предикатов [1]:
. х + 5 = 1
. При х = 2 выполняется равенство х 2 - 1 = 0
. х 2 - 2 х + 1 = 0
. Существует такое число х, что х 3 - 2
. х + 2 < З х - 4
. Однозначное неотрицательное число х кратно 3
. (х + 2) - (3 х - 4)
. х 2 + у 2 > 0
Решение.
1) Предложение является одноместным предикатом Р (х), IP = { - 4};
2) Предложение не является предикатом. Это ложное высказывание;
3) Предложение является одноместным предикатом Р (х), IP ={1};
4) Предложение не является предикатом. Это истинное высказывание;
5) Предложение является одноместным предикатом Р (х), IP = (3; +∞);
) Предложение является одноместным предикатом Р (х), IP = {0; 3; 6; 9};
) Предложение не является предикатом;
) Предложение является двухместным предикатом Q (х,y), IQ = R×R \ { (0,0) }.
Пример 2. Изобразить на декартовой плоскости область истинности предиката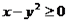 
[2].
Решение. Неравенство, составляющее исходный предикат, ограничивает часть плоскости, заключенную между ветвями параболы х = у 2, она изображена серой частью рисунка:
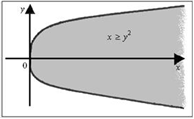
Рисунок 1. График параболы х = у 2
Предикаты, вслед за высказываниями, являются следующим важным предметом, исследуемым математической логикой.
Понятие предиката обобщает понятие высказывания, а теория предикатов представляет собой более тонкий инструмент, по сравнению с теорией высказываний, для изучения закономерностей процессов умозаключения и логического следования, составляющих предмет математической логики [1].
Таким образом, в основном, термин " предикат " понимается в смысле исходного определения, т.е. как языковое выражение. Связано это с тем, что одной из главных целей введения предикатов, как уже отмечалось во введении, является изучение выразительных возможностей логики первого порядка, возможности представления средствами этой логики информации, выраженного на каком - либо естественном языке людей, например, на русском или английском языке.
предикат декартова плоскость математика
Заключение
Логика предикатов, как и традиционная формальная логика, расчленяет элементарное высказывание на субъект (буквально - подлежащее, хотя оно может играть и роль дополнения) и предикат (буквально - сказуемое, хотя оно может играть и роль определения).
Субъект - это то, о чем что - то утверждается в высказывании, а предикат - это то, что утверждается о субъекте. Логика предикатов - это расширение логики высказываний за счет использования предикатов в роли логических функций.
Итак, актуальность темы реферата несомненна. Цель достигнута и задачи выполнены. Литература просмотрена, выбрана, проанализирована, результаты представлены в данном реферате.