Отображение плоскости на себя, при котором все расстояния сохраняются, называется движением,

Тема: Движение

Урок: Понятие движения

Осевая симметрия – это такой тип симметрии, при которой каждой точке плоскости, например в точке М (Рис. 1), по определенному закону ставится в соответствие другая точка той же плоскости.

 

Рис. 1.

Закон, согласно которому проводится это соответствие, таков:

Из точки М проводится перпендикуляр к прямой и получается точка Р, точка пересечения перпендикуляра с осью. Откладывался отрезок РМ₁=РМ, и находится точка М₁. Итак, любой точке М плоскости ставится в соответствие единственная точка М₁ плоскости, при этом:

1. МР^а, Р – точка их пересечения

2. РМ₁=РМ, откуда получалась точка М₁

При этом мы опирались на известный геометрический факт: из точки М можно провести лишь одну прямую перпендикулярную данной прямой.

Обратная операция: если при осевой симметрии точке М ставится в соответствие точка М₁, то точке М₁ ставится в соответствие точка М.

Точно такие же операции соответствия можно провести и для пары точек N и N₁ той же плоскости (Рис. 1), причем если нам известна точка N₁, которая поставлена в соответствие точке N, то нам известна и сама точка N. Итак, каждой точке плоскости ставится в соответствие иная точка плоскости. И любая точка плоскости имеет свою соответствующую точку.

Осевая симметрия является частным случаем так называемого отображения плоскости на себя.

Другим частным случаем отображения плоскости на саму себя является центральная симметрия.

Точка плоскости М переходит в точку плоскости другую М₁ по следующему закону (Рис. 2):

1. проводится прямая МО

2. эта прямая продолжается и на ней откладывается отрезок ОМ₁=ОМ, получаем точку М₁

М₁ ставится в соответствие точке М.

 

 

Рис. 2.

Оба представленных примера отображений обладают следующим свойством:

если взять отрезок MN длиною а, то он перейдет в отрезок M₁N₁ той же длины, т. е. расстояние между любыми точками сохраняются.

Отображение плоскости на себя, при котором все расстояния сохраняются, называется движением,

т. е. «плоскость двигается, а расстояние сохраняется». Движений таких несколько, мы пока рассмотрели два из них, а именно осевую симметрию и центральную симметрию. Теперь докажем, что каждая из этих симметрий является движением. Надо доказать, что любые расстояния сохраняются.

Докажем это для осевой симметрии.

Итак, при от отображении, М → М₁, N → N₁, причем РМ₁=РМ, NQ=QN₁ (Рис. 3)

Нам нужно доказать, что MN= M₁N₁.

 

Рис. 3.

Доказательство.

Составим чертеж (Рис. 4).

Сделаем дополнительные построения, построим точку К такую, что МК^ NN₁,

тогда точка К отобразится в точку К₁.

Докажем равенство прямоугольных треугольников MNК и M₁N₁К₁. В этих треугольниках длины, интересующие нас, являются гипотенузами, значит, надо доказать равенство катетов.

МК = М₁К₁ как два перпендикуляра к параллельным прямым.

Из Рис. 4 видно, что NK = NQ – KQ и N₁K₁ = N₁Q – K₁Q. Из этих равенств и условия того, что точка N отобразилась в точку N₁, вытекает, что NK = N₁K₁.

То есть треугольники равны по двум катетам, а следовательно, равны и их гипотенузы, то есть MN = M₁N₁, что и требовалось доказать.

 

Рис. 4.

Рис. 5.

Докажем теперь, что центральная симметрия также является движением. Дополним Рис. 2 точкой N и точкой N₁, в которую отобразится первая точка при центральной симметрии (Рис. 5).

Для этого построим отрезок ON и его продолжение – отрезок ON₁, получим точку N₁. При этом ON₁ = ON. Необходимо доказать, что MN = M₁N₁

Доказательство.

по двум сторонам и углу между ними ( MОN = M₁ОN₁ как вертикальные, а соответствующие стороны треугольников равны вследствие законов центральной симметрии) .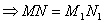

То есть и при центральной симметрии любые расстояния сохраняются. Таким образом, и центральная симметрия является движением.

Итак, мы рассмотрели отображение плоскости на себя. Рассмотрели два примера отображения плоскости на себя: осевую симметрию и центральную симметрию. И подметили одно важное обстоятельство, что любые расстояния при этих преобразованиях сохраняются. Те преобразования плоскости на себя, которые сохраняют все расстояния, называются движениями. Мы доказали, что осевая симметрия является движением и центральная симметрия является движением.

 

Рис. 1.

Пусть имеется некоторая выделенная точка О плоскости. Кроме того, рассмотрим произвольную точку М той же плоскости. Поворотом (обозначение – ) относительно точки О, называемой центром поворота на Ðα (угол поворота) называется такое отображение плоскости на себя, при котором любая точка М плоскости переходит в такую точку М₁ той же плоскости, что ОМ = ОМ₁ и, кроме того, ÐМОМ₁ = α (Рис. 1).

Докажем, что поворот является движением.

Доказательство (Рис. 2).

 

 

Рис. 2.

Рассмотрим точки М и N плоскости, переходящие при повороте соответственно в точки М₁ и N₁ той же плоскости.

Рассмотрим треугольники ОМN и ОМ₁N₁. В этих треугольниках ОМ = ОМ₁ и ОN = ОN₁. ÐМОN = α – ÐМОN₁; ÐМ₁ОN₁ = α – ÐМОN₁, следовательно, ÐМОN = ÐМ₁ОN₁. Таким образом, указанные треугольники равны по двум сторонам и углу между ними. Отсюда вытекает равенство отрезков МN = М₁N₁. Поскольку точки М и N выбирались нами произвольно, можно утверждать, что при повороте длины отрезков сохраняются.

Теорема доказана.

Нам необходимо научиться использовать рассмотренный тип движения.

Задача (аналогичная № 1167 из учебника Атанасян, см. список литературы)

Постройте треугольник, который получается из данного треугольника ABC поворотом вокруг точки А на угол 60° против часовой стрелки ( ∆АВС).

Решение (Рис. 3).

 

Рис. 3.

При повороте точка А перейдет в саму себя. Точки В и С перейдут в точки В₁ и С₁ соответственно. Углы треугольника и длины его сторон, в соответствии с общими свойствами движения, сохранятся (все обозначения сторон и углов даны на Рис. 3).

Построения при повороте крайне простые: при помощи циркуля построить дугу окружности радиусом, равным длине стороны треугольника (АС или АВ), с центром в точке А, далее при помощи транспортира отложить на дуге угол 60° и отметить точку-образ (В₁ или С₁). Соединив полученные точки-образы отрезками, можно получить искомый треугольник А₁В₁С₁, являющийся образом треугольника АВС ( ∆АВС = ∆А₁В₁С₁).

Задача (Атанасян, № 1168).

Точка О является точкой пересечения биссектрис равностороннего треугольника ABC. Докажите, что при повороте вокруг точки О на угол 120° треугольник ABC отображается на себя.

Решение.

Сделаем рисунок (Рис. 4).

 

 

Рис. 4.

Точка О пересечения биссектрис правильного треугольника является центром этого треугольника. Следовательно, вершины треугольника при повороте вокруг точки О будут «отрисовывать» дуги окружности, описанной около ∆АВС. Легко показать, что ÐВОС = ÐСОА = ÐАОВ = 120°. Следовательно, при повороте , точка А перейдет в точку В, точка В перейдет в точку С и точка С перейдет в точку А (напомним, что угол поворота считается положительным, если поворот происходит против часовой стрелки). Таким образом, ∆АВС = ∆АВС.

Задача решена.

Задача. Дана прямая, на которой заданы точка О₁ и точка О₂ и даны точки А и В, лежащие по разные стороны от этой прямой. Причем имеют место равенства расстояний: О₁А = О₁В, О₂А = О₂В.

Доказать, что точки А и В симметричны относительно указанной прямой.

Решение (Рис. 5).

Рис. 5.

Для доказательства требуемого в задаче утверждения нам необходимо доказать, что АМ = МВ и АВ^ О₁О₂.

Построим окружность радиусом О₁А с центром в точке О₁ и окружность радиусом О₂А с центром в точке О₂.

Рассмотрим некоторую осевую симметрию с осью О₁О₂. При таком отображении полуокружности, расположенные в верхней полуплоскости, перейдут в соответствующие полуокружности, расположенные в нижней полуплоскости относительно оси симметрии. При этом точка пересечения «верхних» полуокружностей – точка А – перейдет в точку пересечения «нижних» полуокружностей – точку В. То есть точка В симметрична точке А относительно рассматриваемой прямой. Задача решена.

В заключение разберем еще один простое применение понятий симметрии.

Дан параллелограмм ABCD.

Доказать, что точка пересечения его диагоналей является его центром симметрии.

Напоминание: фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.

Рис. 6.

Решение (Рис. 6).

На рисунке точка О – точка пересечения диагоналей параллелограмма. В силу свойств параллелограмма AО = ОC и BО = ОD, а также любой отрезок, концы которого лежат на противоположных сторонах и проходящий через точку О (например, отрезок MN на Рис. 6), делится в этой точке пополам. Это означает, что при осуществлении центральной симметрии относительно центра, расположенного в точке О, все точки, принадлежащие сторонам, перейдут в точки, также принадлежащие сторонам. Таким образом, параллелограмм перейдет сам в себя, т. е. точка О – центр симметрии.

Подведем итоги: на данном уроке мы ввели в рассмотрение новый вид отображения плоскости на себя – поворот, доказали, что он является движением и решили ряд задач, которые помогут лучше понять изучаемую тему.