Урок
Задание: изучить материал урока и выполнить домашнее задание.
Информационная карта
Тема: Уравнения с двумя переменными.
Цель: рассмотреть решения уравнений с двумя переменными.
Теоретический минимум
Определение. Линейным уравнением с двумя переменными называется уравнение вида
mx + ny = k, где m, n, k – числа, x, y – переменные.
Пример: 5x+2y=10
Определение. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Уравнения с двумя переменными, имеющими одни и те же решения, называются равносильными.
1. 5x+2y=12 
(2)y = -2,5x+6
Данное уравнение может иметь сколько угодно решений. Для этого достаточно взять любое значение x и найти соответствующее ему значение y.
Пусть x = 2, y = -2,5•2+6 = 1
x = 4, y = -2,5•4+6 =- 4
Пары чисел (2;1); (4;-4) – решения уравнения (1).
Данное уравнение имеет бесконечно много решений.
Историческая справка
Неопределенные (диофантовы) уравнения – это уравнения, содержащие более одной переменной.
В III в. н.э. – Диофант Александрийский написал “Арифметику”, в которой расширил множество чисел до рациональных, ввел алгебраическую символику.
Так же Диофант рассмотрел проблемы решения неопределенных уравнений и им даны методы решения неопределенных уравнений второй и третьей степени.
Определение: Неоднородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = k, где m, n, k, x, y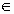 
Z k 
0
Утверждение 1.
Если свободный член k в уравнении (1) не делится на наибольший общий делитель (НОД) чисел m и n, то уравнение (1) не имеет целых решений.
Пример: 34x – 17y = 3.
НОД (34; 17) = 17; 3 не делится нацело на 17, в целых числах решения нет.
Пусть k делится на НОД (m, n). Делением всех коэффициентов можно добиться, что m и n станут взаимно простыми.
Утверждение 2.
Если m и n уравнения (1) взаимно простые числа, то это уравнение имеет по крайней мере одно решение.
Утверждение 3.
Если коэффициенты m и n уравнения (1) являются взаимно простыми числами, то это уравнение имеет бесконечно много решений:
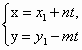где (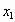
; 
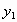) – какое-либо решение уравнения (1), t 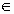Z
Определение. Однородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = 0, где (2)
m, n, x, y 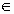Z
Утверждение 4.
Если m и n – взаимно простые числа, то всякое решение уравнения (2) имеет вид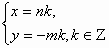 
Методы решения уравнений
I. Метод рассмотрения остатков от деления.
Пример. Решить уравнение в целых числах 3x – 4y = 1.
3x = 4y + 1.
Левая часть уравнения делится на 3, следовательно, должна делиться и правая часть. Рассмотрим три случая.
- Если y = 3m, m 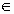Z, то 4y + 1= 4•3m + 1 = 12m + 1 не делится на 3.
- Если y = 3 m + 1, то 4y +1 = 4• (3m + 1)+1 = 12m + 5 не делится на 3.
- Если y = 3 m + 2, то 4y +1 = 4• (3m + 2)+1 = 12m + 9 делится на 3, поэтому 3x = 12m + 9, следовательно, x = 4m + 3, а y = 3m + 2.
Ответ: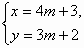 
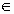где m Z.
Описанный метод удобно применять в случае, если числа m и n не малы, но зато разлагаются на простые сомножители.
Пример: Решить уравнения в целых числах.
8x + 14y = 32
4x + 7y = 16
4x = 16 – 7y
Пусть y = 4n, тогда 16 - 7y = 16 – 7•4n = 16 – 28n = 4*(4-7n) делится на 4.
y = 4n+1, тогда 16 – 7y = 16 – 7• (4n + 1) = 16 – 28n – 7 = 9 – 28n не делится на 4.
y = 4n+2, тогда 16 – 7y = 16 – 7• (4n + 2) = 16 – 28n – 14 = 2 – 28n не делится на 4.
y = 4n+3, тогда 16 – 7y = 16 – 7• (4n + 3) = 16 – 28n – 21 = -5 – 28n не делится на 4.
Следовательно, y = 4n, тогда
4x = 16 – 7•4n = 16 – 28n, x = 4 – 7n
Ответ: 
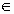, где n Z.
II. Неопределенные уравнения 2-ой степени
Сегодня на уроке мы лишь коснемся решения диофантовых уравнений второго порядка.
И из всех типов уравнений рассмотрим случай, когда можно применить формулу разности квадратов или другой способ разложения на множители.
Пример: Решить уравнение в целых числах.
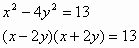
13 – простое число, поэтому оно может быть разложено на множители лишь четырьмя способами: 13 = 13•1 = 1•13 = (-1)(-13) = (-13)(-1)
Рассмотрим эти случаи
 |
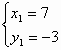а)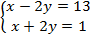 
=>
б)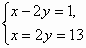 
=> 
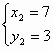
в)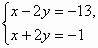 
=> 
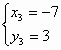
г) 
=> 
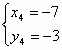
Ответ: (7;-3), (7;3), (-7;3), (-7;-3).